WAH－B 样条曲线①

王明星， 谢 进， 王寿城

(1．合肥工业大学数学学院，安徽合肥230009;2．合肥学院数理系，安徽合肥230601)

1 引言

B样条曲线和曲面是计算机辅助几何设计(CAGD)中常用的工具之一．但由于它在实际运用当中有很多的局限性[1]，因此，不少作者[2－9]中引入了一系列新的几何曲线和曲面模型．文献[2－4]提出CB样条，实际上和文献[5]中提出的螺旋样条是类似的．C曲线可以精确逼近椭圆曲线，旋轮线和螺旋线．文献[6]提出了通过一组基{1，t，cosht，sinht}的生成子空间 {1，t，cosht，sinht}来构造指数样条．文献[7]在空间 {1，t，cosht，sinht}满足张量运算下，提出了一类指数样条．文献[8]给出了均匀样条的精确表达式．文献[9]将曲线和曲面的指数形式推广到了任意次数的代数双曲样条形式上．这类曲线可以精确逼近双曲线和悬链线．除此之外，这类曲线的微积分计算非常的简单．但是，指数形式的样条在张量积下是不能逼近高次多项式曲线的，这就严重的限制了它们在CAGD中的应用．实际上，目前三次曲线在CAGD中应用的最广，并且文献[10－13]给出了三次曲线非常重要的几何性质．文献[14－15]提出了用两组基 {1，t，cosht，sinht}和 {1，t，cosht，sinht}来构造曲线族，并将这类曲线族中的曲线称为FB样条．FB样条几乎拥有CB样条和HB样条的所有性质，比如说，连续性等性质．然而，FB样条的表达式却十分的复杂．文献[16]归纳和推广了三类样条曲线，从而得到了定义在空间 {cosωt，sinωt，1，t，…，tl，…}中的一类新的样条(简称为UE样条)．这类样条的好处是，只要改变序列{ωi}就可以得到不同的样条．

本文提出一类新的基函数，这类基函数是对三次 B 样条曲线的基 {1，t，t2，t3}与双曲基 {1，t，cosht，sinht}经过加权而得到．这类基函数继承了三次B样条曲线拥有的大部分性质．根据这类基，本文得到了一类新的样条曲线，称为WAH－B样条曲线．这种方法具有如下性质:

*这类曲线既能整体地又能局部地改变形状．

*取权参数的值为，可以不用解方程组，曲线能直接插值于插入给定的控制顶点．

*选取权参数及适当的控制顶点，WAH－B样条曲线可精确表示圆锥曲线和超曲线．

*令权参数λi=0或1，可以改变曲线的类型，并且，一段混合样条曲线可以不同类型曲线组合形成．

2 WAH－B样条基函数定义

定义2．1 设0≤λi，λi+1≤1，将下面的函数．称为带权参数序列{λk}的WAH－B样条基函数．

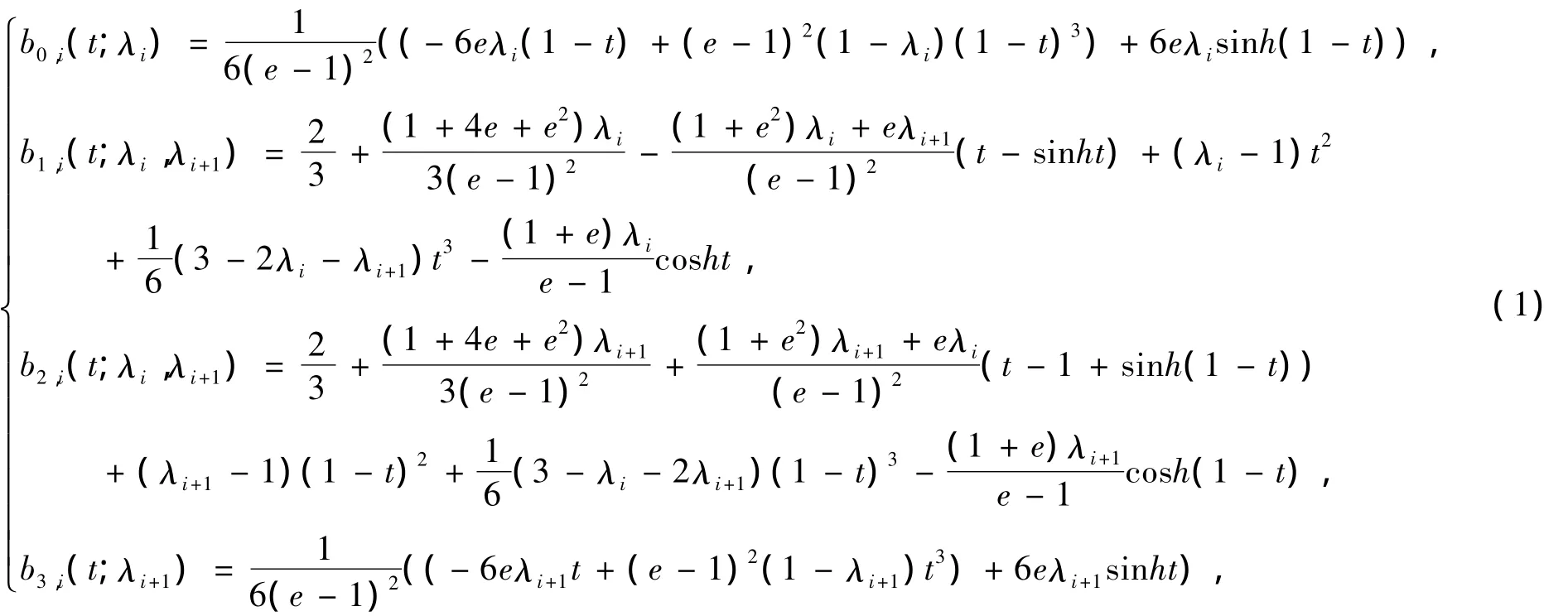
很明显，当所有的λi=0时，WAH－B样条基函数就是三次B样条基函数．当所有的λi=1时，WAH－B样条基函数就是α=1的4阶双曲多项式B样条基函数[8]．

直接计算可以证明，WAH－B样条基函数拥有类似于三次B样条基函数的性质．

A．归一性

B．非负性．

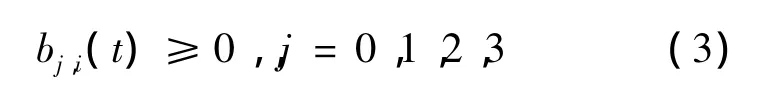
C．对称性．

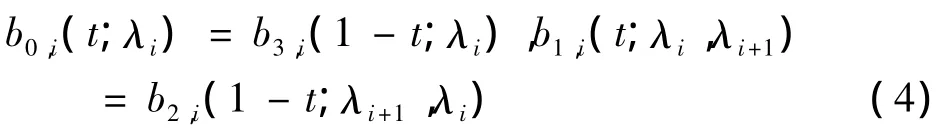
根据文献[17]中给出的扩展C曲线的定义域的方法，WAH－B样条基函数中权因子的取值范围可以扩展到区间上．其中

图1给出了三次B样条基函数(实线)与WAH－B样条基函数，其中图a中的权参数取相同值，图b权参数取不同值．

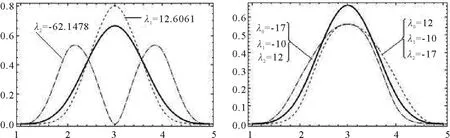
图1 样条基函数的图像

3 样条曲线

3．1 构造曲线

定义3．1 给出控制点Pi∈Rd(d=2，3，i=0，1，2，…，n)和结点u1＜u2＜ … ＜un－1，其中u∈[ui，ui+1]，i=1，2，…，n－2，称曲线为WAH－B样条曲线．其中

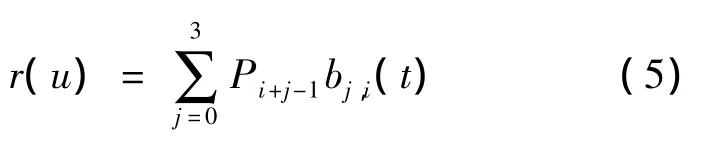
与三次B样条曲线一样，我们可以构造一个开WAH－B样条曲线和一个闭WAH－B样条曲线．对于开曲线，若设λi，u0＜u1，un－1＜un，P－1=2P0－P1，Pn+1=2Pn－Pn－1就可以保证初始点P0和Pn在曲线上，即r(u0)=P0，r(un)=Pn．对于闭曲线，我们可以周期性的设控制点满足Pn+1=P0，Pn+2=P1，Pn+3=P2，以及设结点满足un－1＜un＜un+1＜un+2．其中 λi∈，i=n，n+1，n+2，λ1=λn+2．

3．2 曲线的性质

3．2．1 连续性

曲线(5)是由代数与双曲多项式加权混合而成．因此，需要证明该曲线具有连续性．

定理3．1 设u∈[u1，un－1]，曲线(5)是GC2连续的．均匀曲线(5)是C2连续的．

证明: 当i=1，2，…，n－1时，可以得到

结合上面的等式，有

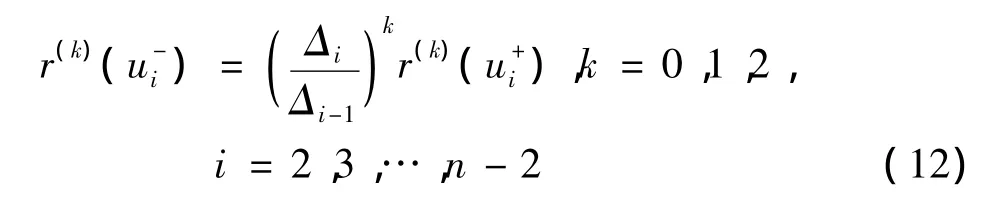
证毕．

根据式(8)和(9)，我们发现曲线r(u)在点r(ui)处的切线与线段Pi－1Pi+1(对任意的λi)平行．这条性质与三次均匀B样条曲线的性质是一致的．3．2．2 局部与整体可控性

设u∈[ui，ui+1]，将式(5)变形，有

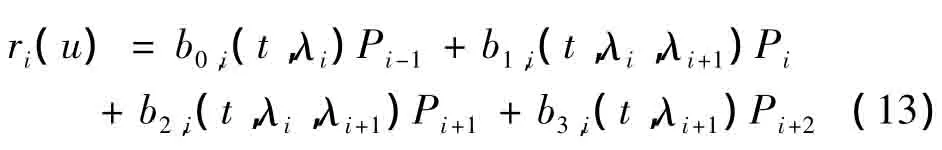
显然，权参数λi只会影响两条曲线段ri－1(u)和ri(u)，而不会影响其它的曲线段．即，权参数λi只会影响控制多边形．因此，只有改变 λi的值，就可以局部地改变曲线的形状．从图2(a)中，可以发现，曲线r(u)(u∈[ui－1，ui+1])会随着λi的增加向控制多边形靠拢，r(u)随着λi的减小而远离控制多边形

当λi取相同值时，可以整体调控曲线的形状．从图2(b)中，可以看出，当控制多边形固定时，加权因子从－62．1748到12．6061范围内动态变动时，WAH－B样条曲线可以从两侧逼近三次B样条曲线．并且，权参数具有这样的性质:加权因子取值越大，曲线就越逼近控制多边形．

图2 曲线形状的调控

3．2．3 局部与整体插值

曲线(6)也可以用于局部插值．设 λi=，由式(6)和(7)，可以推出r(ui)=Pi．即，曲线r(u)在u=ui处的插值结点是Pi．因此，这就提供了一种求解GC2连续的局部插值法．用这种方法，可以不用求解方程组或者为了求解的需要，而刻意的增加控制点．用WAH－B样条曲线可以局部地插值于给定的控制点．特别地，当所有的时，曲线可以整体地插值于控制多边形．

4 一些圆锥曲线和超越曲线的表示

4．1 双曲线和抛物线的表示

定义4．1 设节点是均匀节点，且P0，P1，P2和P3是如下定义的四个控制顶点．

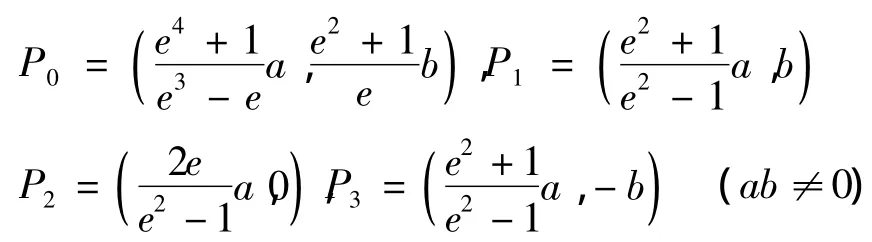
当u∈[ui，ui+1]，权参数λi=λi+1=1时，WAH －B样条曲线可以表示一条抛物弧线．

证明: 将P0，P1，P2和P3代入式(5)中，将会得到WAH－B样条曲线的坐标形式，

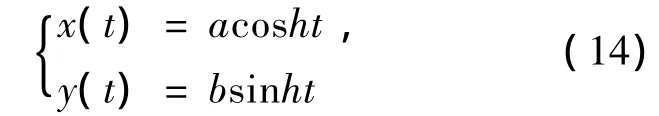
这是双曲线的一个参数方程，如图4所示:

图3 整体和局部插值曲线

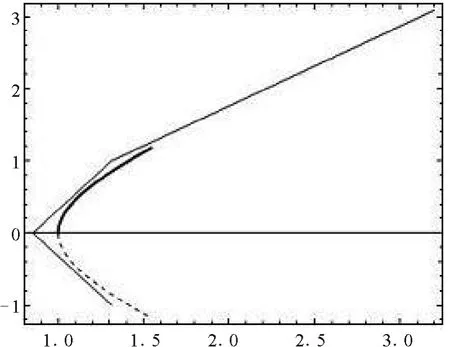
图4 用WAH－B样条曲线表示双曲线

定义4．2 设P0，P1，P2和〛P3是如下所示的四个控制点

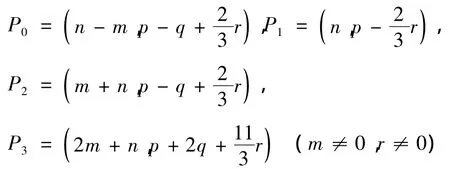
当u∈[ui，ui+1]，权参数λi=λi+1=0时，WAH －B样条曲线可以比表示抛物线的一部分

证明: 将P0，P1，P2和P3代入式(5)将会得到WAH－B样条曲线的下面坐标形式，

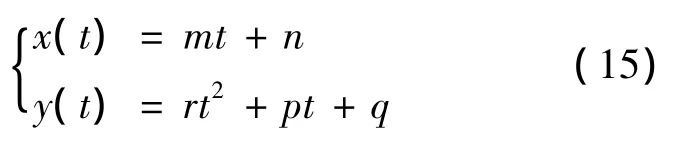
这是抛物线的一个参数方程，如图5所示:

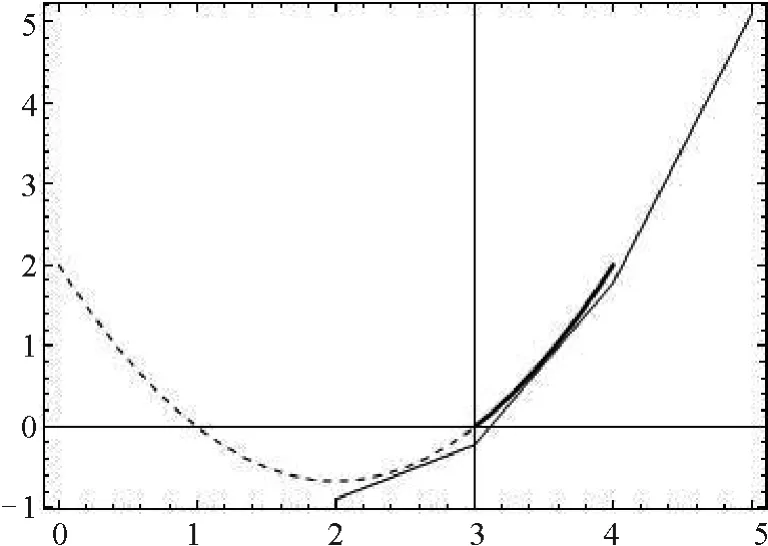
图5 用WAH－B样条曲线表示抛物线

4．2 悬链线和双曲正弦曲线的表示

定义4．3 设四个控制点如下所示，

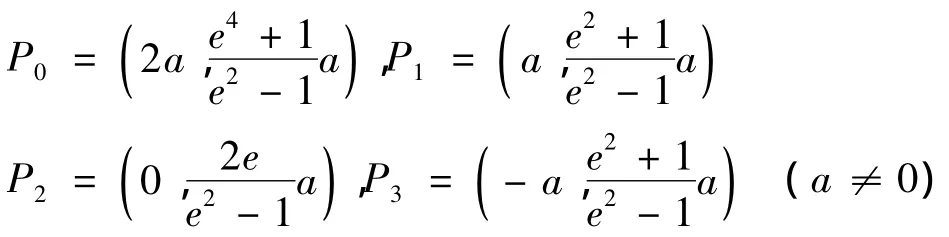
当u∈[ui，ui+1]，权参数 λi=λi+1=0 时，WAH －B样条的曲线可以表示悬链线的一部分．

证明: 通过将点P0，P1，P2和P3代入式(5)，我们将会得到WAH－B样条曲线的如下坐标表示，

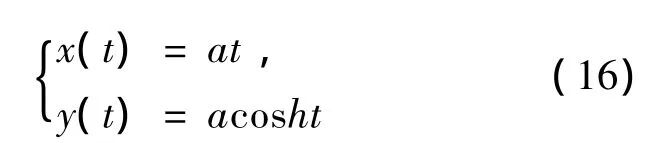
显然，它是悬链线的一部分，如图6所示:

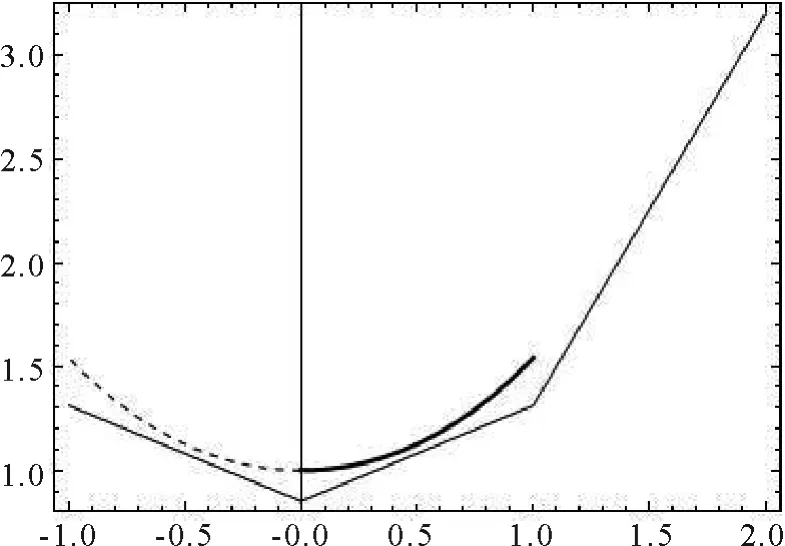
图6 用WAH－B样条曲线表示悬链线

定义4．4 设节点是均匀的，且P0，P1，P2和P3是如下所定义的四个控制点，P0=(－1，－1)，P1=(0，1)，P2=(1，1)，

P3=(1，e+e－1)

当u∈[ui，ui+1]，权参数 λi=λi+1=0 时，WAH－B样条曲线可以表示双曲正弦线的一部分．

证明: 通过将P0，P1，P2和P3代入式(5)中，我们将会得到WAH－B样条曲线的如下表示

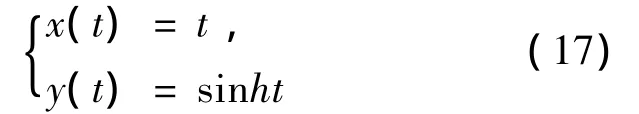
这是在参数坐标下的双曲正弦线，如图7所示:

图7 用WAH－B样条曲线表示双曲正弦线

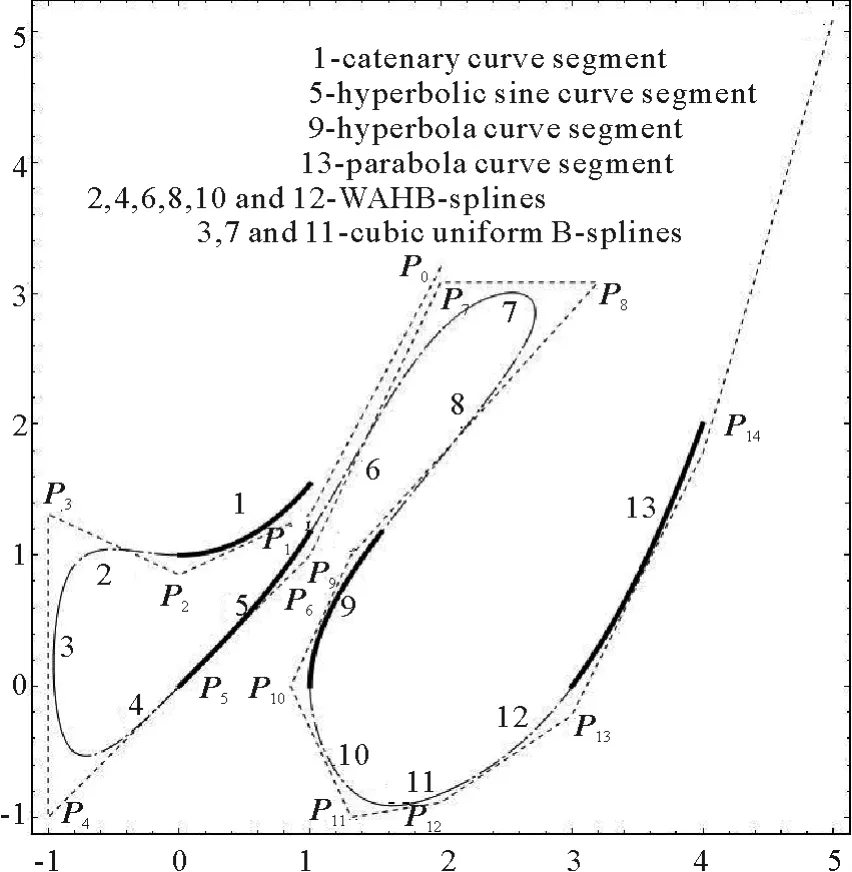
图8 C2连续的混合曲线

5 曲线的应用

正如在第4部分所提到的，可以通过选择适当的控制点和参数来改变曲线的形状．因此，我们可以灵活的应用不同类型的部分曲线来构造混合曲线．例如，当取均匀节点及参数 λi=(1，1，0，0，1，1，0，0，1，1，0，0，1，1，0，0)时，其中i=1，2，…，16，如下定义控制顶点，

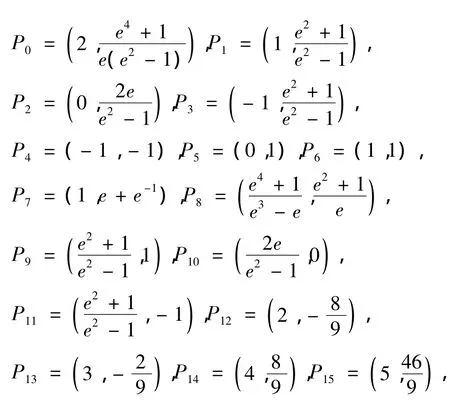
因此我们得到了一个由不同类型的曲线构成的混合曲线，且它是一个C2连续的，如图8所示:

6 结 论

本文通过三次B样条基函数 {1，t，t2，t3}和双曲基函数{1，t，cosht，sinht}来构造WAH －B样条曲线．在权参数取值范围内，该曲线可以从两侧逼近三次B样条曲线．并且这种曲线可以插值于给定的控制点．特别地，当权参数λi=0或1时，这些曲线可以改变为不同类型的曲线．

与用有理方法生成的非均匀有理B样条曲线或有理Bézier曲线[19]相比，WAH －B样条曲线在结构上更加简单，及计算上更加稳定．WAH－B样条曲线的权参数具有明显的几何的意义．WAHB样条曲线能够精确表示螺旋线、轮转线和悬链线，而非均匀有理B样条曲线或有理Bézier曲线只能近似表示．因此，WAH－B样条曲线在工程方面有着更好的应用．

[1] Mainar，E．，Pea，J．M．，Snchez － Reyes．Shape Preserving Alternatives to the Rational Bézier Model[J]．Computer Aided Geometric Design，2001，18，37–60．

[2] Zhang，J．W．C － curves:An Extension of Cubic Curves[J]．Computer Aided Geometric Design，1996，13:199–217．

[3] Zhang，J．W．Two Different Forms of C － B － splines[J]．Computer Aided Geometric Design．1997，14:31 –41．

[4] Zhang，J．W．C － Bézier Curves and Surfaces[J]．Graphical Models and Image Processing，1999，61:2–15．

[5] Pottmann，H．，Wagner，M．G．Helix Splines as Example of Affine Tchebycheffian Splines[J]．Advance in Computational Mathematics，1994，2，123–142．

[6] Pottmann，H．The Geometry of Tchebycheffian Spines[J]．Computer Aided Geometric Design，1993，10:181 –210．

[7] Koch，P．E．，Lyche，T．Exponential B － splines in Tension[M]．In:Chui，C．K．，Schumaker，L．L．，Ward，J．D．(Eds．)，Approximation Theory VI．Academic Press， New York，1989，p．361 －364．

[8] Lü，Y．G．，Wang，G．Z．，Yang，X．N．Uniform Hyperbolic Polynomial B － spline Curves[J]．Computer Aided Geometric Design，2002，19(6):379－393．

[9] Li，Y．J．，Wang，G．Z．Two Kinds of B Basis of the Algebraic Hyperbolic Space[J]．Journal of Zhejiang University Science A，2005，6:750－759．

[10] Hoffmann，M．，Juhász，I．Geometric Aspects of Knot Modification of B － spline Surfaces[M]．J．Geom．Graph．，2003，6:141－149．

[11] Hoffmann，M．，Juhász，I．On the Family of B － spline Surfaces Obtained by Knot Modification[C]．Mathematical Communication，2006，11:9－16．

[12] Hoffmann，M．，Li，Y．J．，Wang，G．Z．Paths of C － Bézier and C －B － spline Curves[J]．Computer Aided Geometric Design，2006，23(5):463－475．

[13] Juhász，I．，Hoffmann，M．Constrained Shape Modification of Cubic B － Spline Curves by Means of Knots[J]．Computer Aided Design，2004，36(5):437－445．

[14] Zhang J．W．，Krause F．－L．Zhang H．Y．Unifying C －curves and H－Curves by Extending the Calculation to Complex Numbers[J]．Computer Aided Geometric Design，2005，22:865–883．

[15] Zhang，J．W．，Krause，F．－ L．，Extend Cubic Uniform B －splines by Unified Trigonometric and Hyperbolic Basis[J]．Graphic Models，2005，67(2):100–119．

[16] Wang，G．Z．Fang，M．E．Unified and Extended Form of Three Types of Splines[J]．Journal of Computational and Applied Mathematics2008，216:498 – 508．

[17] Lin S．H．，Wang G．Z．Extension of Definition Interval for C －Curves[J]．Journal of Computer Aided Design and Computer Graphics，2005，17(10):2281～2285(in Chinese)．

[18] Han X．L．Piecewise Quartic Polynomial Curves with a Local Shape Parameter[J]．Journal of Computational and Applied Mathematics．2006，195(1):34 －45．

[19] Farin，G．Curves and Surfaces for Computer Aided Geometric Design[M]．4th ed．Academic Press，San Diego，1997，CA．