一类递推数列极限存在的充分条件

崔玉娟

（95962部队，江苏徐州 221000）

数列、极限［1］与数学归纳法［2－4］是中学数学的重要内容，是与大学衔接较紧的内容之一，也是进一步学习高等数学不可少的基础。因而历来高考“市场”上出现较多“热门货”，这也是对能力要求较高，学生难以得手的“紧俏商品”。递推数列的极限求解问题在历年的考研题中屡次出现。文献［5－6］分别给出了与极限的例子，文中给出了这类问题的较一般的情形（n＝1，2，…）极限存在的充分条件。

命题 设｛xn｝由递推关系（n＝1，2，…）确定，其中a＞0，则当b，x0满足1）或2）。

2＜b＜＋∞

时，有

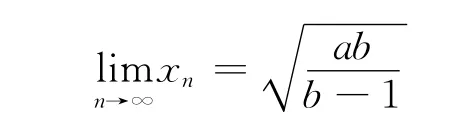
1）因为

所以

进而

从而｛xn｝单调。因为

所以

x1＞x0

故｛xn｝递增。

下证｛xn｝有上界。我们可得x1＜l。因为

所以

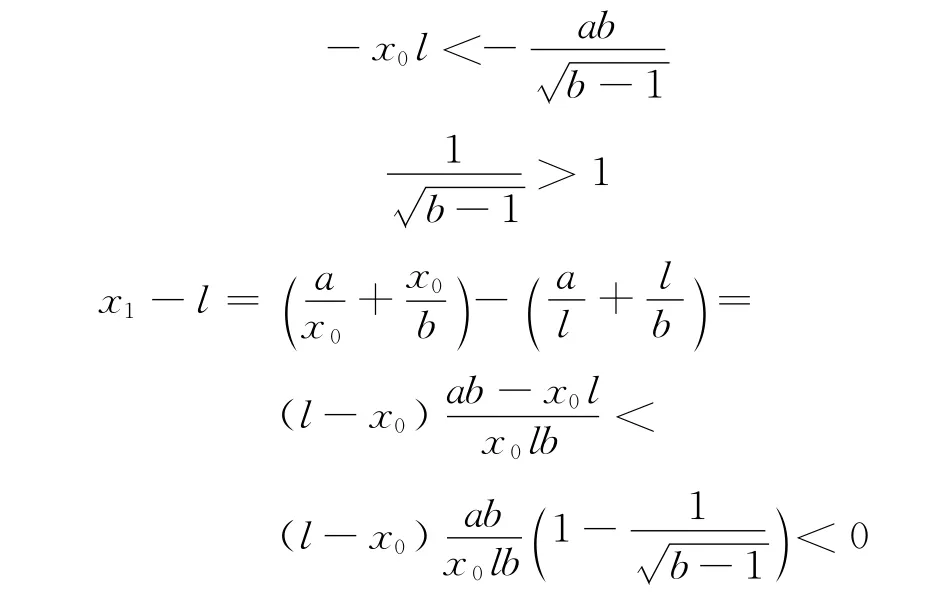
假设xk＜l，因为

补偿额度：建议补偿额度综合考虑需量机组和现有火电机组的维持需求，原则上补偿额度以补偿需量机组的全成本为主，当不足以覆盖现有火电机组维持需求时进行一定扶持。

所以

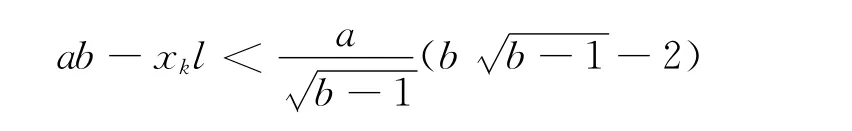
令

则

令

则

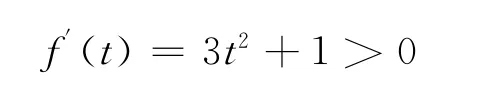
所以f（t）递增，f（t）＜f（1）＝0，进而ab－xkl＜0。则

故xk＋1＜l。由数学归纳法得xn＜l，即｛xn｝有上界l。

2）由l＜x0＜得l2＜＜ab，从而（1－b）＜（1－b）l2＝－ab。可得x1＜x0，因为

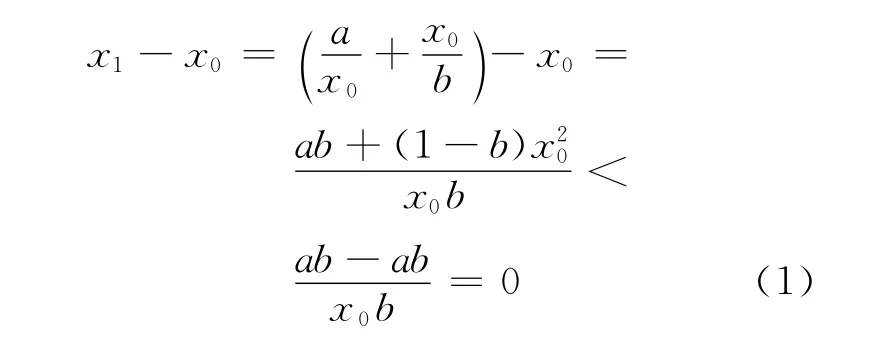
可得0＜x1＜l，这是因为l＜x0＜

从而

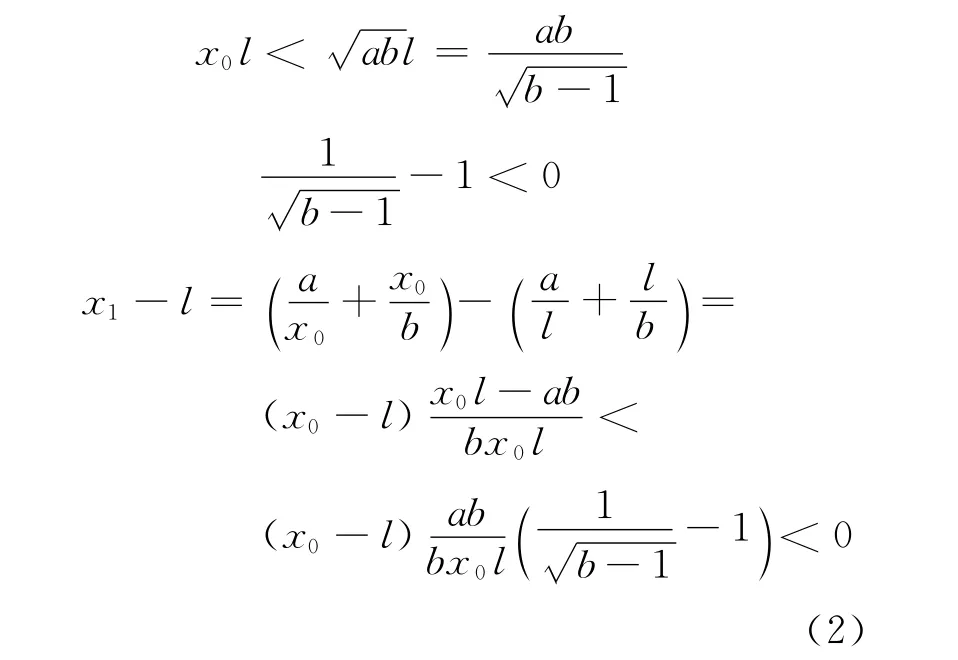
进而得x1＜x2，这是因为

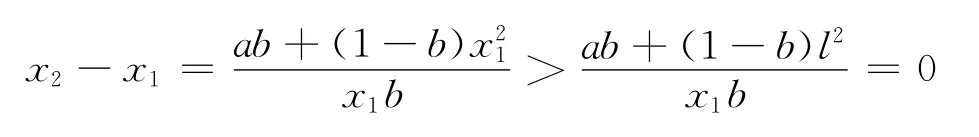
我们有l＜x2＜，x3＜x2，这是因为0＜x1＜l，b＞2所以

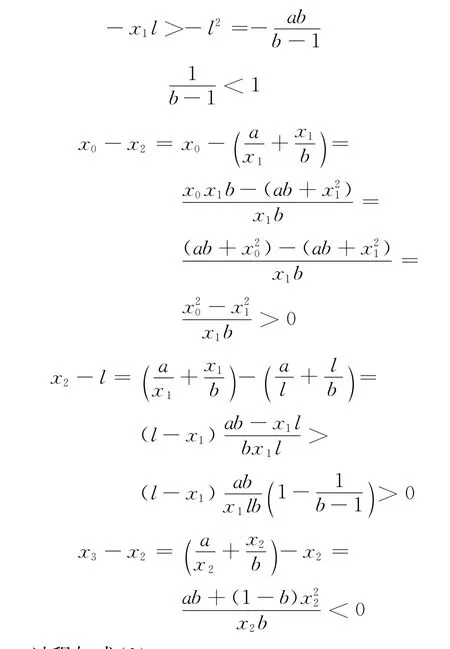
过程如式（1）。

还可得x1＜x3＜l，这是因为

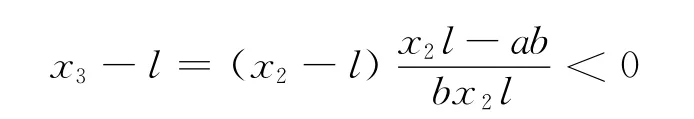
过程如式（2）。

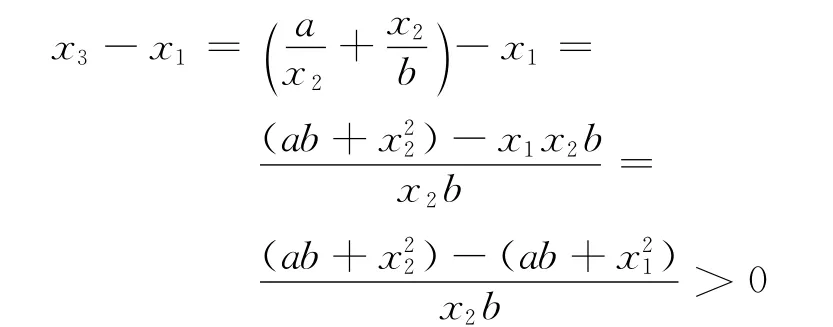
由数学归纳法得

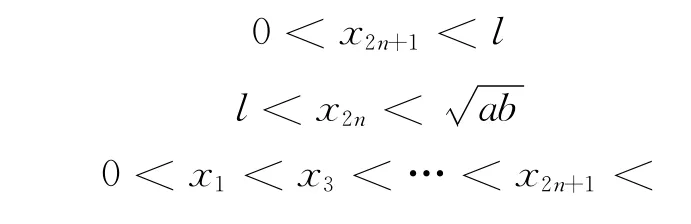
即｛x2n｝单调有界，｛x2n＋1｝单调有界。故它们极限存在，分别设为A，B，则有

解得A＝B。所以｛xn｝极限存在。

由上述证明知，在情形（1），（2）下，｛xn｝极限存在。不妨设为L，两边取极限得

解得

负值舍去，因为｛xn｝是正数列。

［1］ 刘玉琏，数学分析讲义［M］．北京：高等教育出版社，2001．

［2］ 华罗庚．数学归纳法［M］．北京：科学出版社，2002．

［3］ 张和瑞，郝柄新．高等代数［M］．北京：人民教育出版社，1979．

［4］ 北京大学数学系．高等数学［M］．北京：高等教育出版社，1998．

［5］ 王戈平．数学分析选讲［M］．徐州：中国矿业大学出版社，2002：50－51．

［6］ 华东师范大学数学系．数学分析［M］．北京：科学出版社，2002：38－39．

［7］ T H阿里波夫，B A萨多夫尼奇，B H丘巴里阔夫．数学分析讲义［M］．3版．北京：高等教育出版社，2006：24－25．

［8］ 刘玉链．数学分析讲义练习题选解［M］．北京：高等教育出版社，1996．