基于独立分量分析和支持向量机的气液两相流流型识别

周云龙，顾杨杨

(东北电力大学能源与动力工程学院，吉林吉林132012)

气液两相流广泛的存在于工程和自然界中，与人类的生活和生产密切相关。目前，在化工、石油、能源、冶金、环保和轻工等行业的许多生产设备中都涉及两相流工况，而两相流学科是以两相流系统为研究对象，与数学、力学、信息、生物、环境、材料和电子计算机等学科相互融合交叉而逐步形成和发展起来的一门新兴交叉学科［1］。流型的识别一直是两相流研究的重中之重。传统的流型识别方法一般分为两类:一是直接法即根据两相流流动图像的形式直接确定流型;二是间接法即是通过对反应流型特性的参数进行特征提取，后通过其他的识别系统以达到流型识别的目的。在文献［2］中将独立分量分析的方法应用于故障诊断的特征提取中，但并没有将其应用于流型识别中。本文的创新点在于首次将独立分量分析法应用于流型识别的特征提取过程中。

近年来，信息技术和测量技术的快速发展为气液两相流的智能识别提供了重要的技术手段。而神经网络［3］的发展作为一种智能的识别技术已经在流型识别的过程中得到了广泛的应用，应用的主要形式集中在BP、RBF神经网络［4］上。但是，由于神经网络往往存在过学习的问题，产生的模型有时也会产生过度拟合，或拟合程度较差的现象，而支持向量机恰好可以弥补这个不足。支持向量机(Support Vector Machine，SVM)是AT＆Be ll实验室Vapnik V针对分类和回归问题(Classification and Recognition)提出的［5］，此方法一经提出就得到了广泛的关注，并成功的应用于多个领域。在本文中将独立分量分析技术与支持向量机相结合，由此提出了一种新的流型识别方法，经试验证明该方法可以很好的识别出泡状流、间歇流、分层流和环状流这四种流型，具有很好的识别准确率，可以满足工程要求，为流型的识别提供了一种新的技术手段。

1 流型的特征提取

1.1 方法简介

独立分量分析(Independent Component Analysis，ICA)是近几年发展起来的一种新的信号处理技术［6］，它是盲源分离技术的一种延伸。ICA算法的基本思路是:从多个未知的源信号的线性混合信号中分离出相对独立的源信号。

由图1可知［7］，ICA算法的目标是寻找一个矩阵B(n*m)，使得经过y=B*x后得到的各个独立分量之间没有相关性，即尽可能的相互独立，这时的y可以看作是对源信号的最优逼近。在进行此方法的时候一般需要进行如下假设［8］:

(1)m=n，观测到的信号个数与源信号个数相同，解混矩阵为方阵;

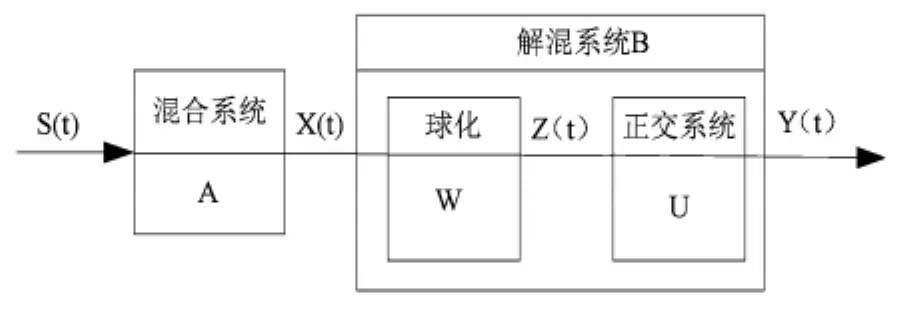
图1 ICA的混合-解混过程简图

(2)s中最多只包含一个高斯分量;

(3)假设模型无噪声;

(4)矩阵A是非奇异的。

由于负熵作为高斯性度量的效果比累积量更具优越性，因此本文采用基于负熵的FastICA算法对流型进行特征提取［9］。

1.2 基于负熵的ICA法对流型进行特征提取

1.2.1 数据的白化处理

首先对收集到的四种流型的压差波动信号进行处理，使其具有零均值、单位方差，其具体的步骤如下:

(1)将源信号S(t)去均值:

(2)根据图1中的过程对数据进行球化:

或简记作:

式中:A是M*N混合矩阵。

(3)在解混过程中可以分为两步，第一步先把观察矢量x(t)经线性系统W变换成中间输出z(t);第二步再把z(t)变换成y(t)［10］。要求z(t)中各分量均经过正交归一化(即互相正交而且方差都等于1):

称这一步为“球化”(sphering)［11］，得到的z(t)就是可以满足零均值和单位方差的数据。

计算标准差:

1.2.2 负熵的引入

熵可以用于定义一种非高斯性度量。可以简单地从微分熵得出一种度量，称为负熵［12］，它对高斯变量是零，并且永远是非负的。负熵J的定义如下:

式中:xgauss是和x具有相同的协方差矩阵∑的某个高斯随机变量。它的熵可以计算出来，即

式中:n是x的维数。

负熵的一个重要性质是:对于可逆的线性变换保持不变。在ICA中，该性质使得可以将边缘负熵J(Yi)作为代价函数，然后寻找线性变换W使其最大化。这就导致了ICA算法中负熵判据的有效性。在本文中输出量y基于高阶矩表示最大熵准则估计法的形式是:

其中，m是具有零均值和单位方差的高斯变量，函数Fi(·)为非二次函数，而其选择的形式通常有以下三种:

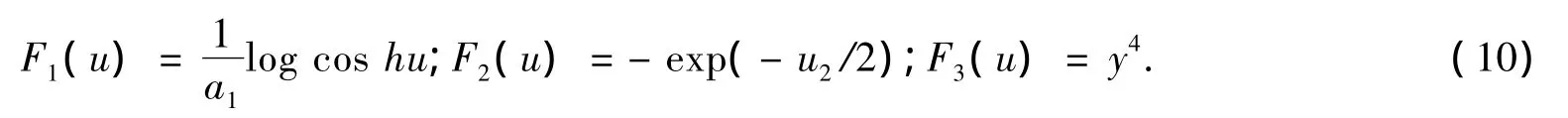
常数a1的取值范围是1≤a1≤2，通常取1。基于负熵的快速不动点算法的原理是寻找一种使非高斯性可以达到最大值的不动点迭代方法，W为输入向量z的权矢量。在进行迭代算法时选择F(u)=log cos u，它的导数f(y)=tanhy，初始迭代为w=E［zf(wTz)］，但未达到理想的收敛条件，对其进行调整:

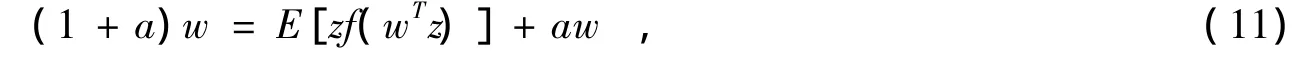
进行归一化:

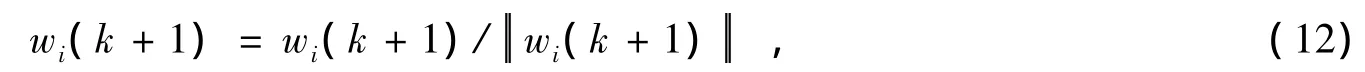
由于数据已经是经过白化后的数据，因此采用牛顿迭代法进行求解，得到基于负熵的快速不动点ICA算法的迭代公式:

1.2.3 算法步骤

(1)将X去均值;

(2)对数据进行球化处理得到Z;

(3)任意选择wi的初值wi(0)，并要求初值满足条件:wi(0)2=1;

(6)如果未收敛返回(4);否则结束。

经过以上步骤后分别以流型的归一化数据、球化数据、标准差以及独立分量这四个参数作为神经网络的样本输出到RBF神经网络中进行流型的识别。

2 支持向量机

支持向量机(Support Vector Machine，简称SVM)［13］是统计学研究中最实用的部分。直到1992-1995年间它的主要内容才基本完成，目前仍处于发展阶段。支持向量机的基本思想可以简单的理解为:首先通过内积(核)函数将输入空间变换到一个高维的空间中;然后在新空间中寻找最优线性分类超平面即可。支持向量机求得的分类函数类似于神经网络，其输出是由若干个中间层节点的线性组合，而每一个中间层节点对应于输入样本与一个支持向量的内积，因此也可以称之为支持向量网络，见图2［14］。

图2 支持向量机示意图

首先用一个非线性映射 φ(x)=［φ1(x)，…，φN(x)］，把输入数据从原始空间映射到N维特征空间，在特征空间构造最优分类超平面见图3，寻找最大的距离使分类间距最大的优化问题表示为:

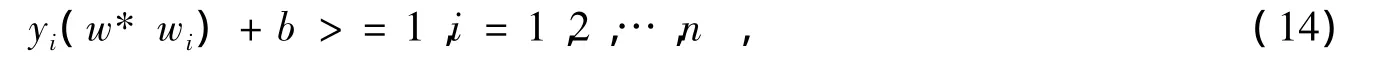
的约束条件为求(13)式的最小值为:

该问题可以利用拉格朗日乘子方法将其转化为对偶问题来解决，即在:

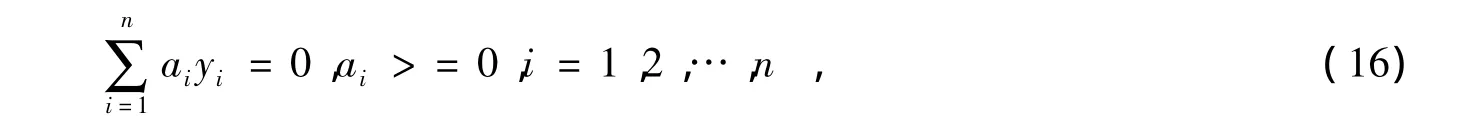
的约束条件下求:

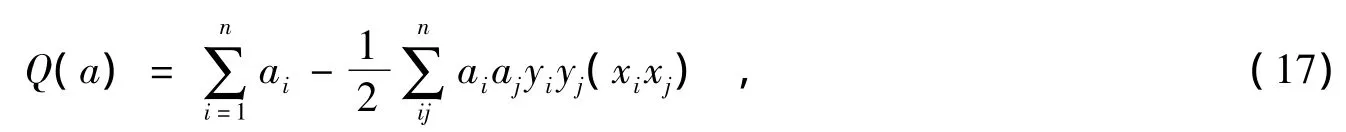
2.1 支持向量机的优化

对于标准的支持向量机他的优化问题是:

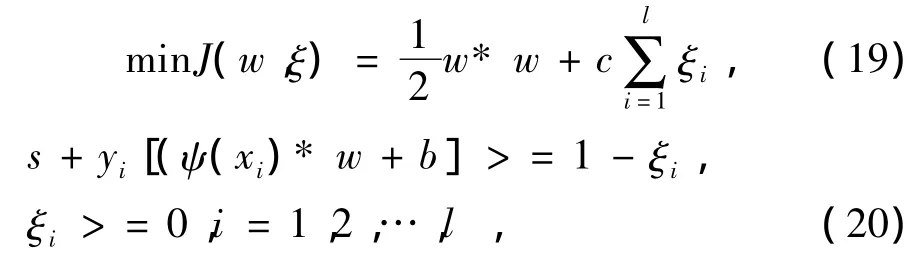
图3 最优分类面

对独立分量分析提取出的特征参数x进行归一化处理:

经过归一化后使数据位于［0，1］的范围内。令“+1”表示“有”，“-1”表示“无”。

2.2 核函数的选择

支持向量机的成功取决于两个方面:第一项是最优分界面;第二项就是核函数，这也是一个很受欢迎的研究领域。常用的满足Mercer条件［15］的核函数主要有线性核函数、多项式核函数、径向基(RBF)核函数和Sigmoid函数等，当选择不同的核函数时就可以产生不同的支持向量机。他们的函数形式可以表示如下:

式中:v，r均d为核参数。

其中的RBF核函数［16］(也称为高斯核函数)较为常用，可以将其定义为空间中任一点Xi到某一中心Xj之间欧式距离的单调函数。因此在本文中选择了较常用的RBF核函数，构造的支持向量机判别函数是:

其中，s是支持矢量xi可确定径向基函数的中心，s是中心的数目。

2.3 算法步骤

本文中将独立分量分析技术与支持向量机相结合形成了一种新的组合式的分类器，首先用ICA法对数据进行处理，提取出独立的分量作为特征参数，并建立学习样本作为分类器的输入，再利用支持向量机建立分类模型［17］，以完成分类的目的。其具体步骤可以描述为以下三个方面:

(1)特征参数提取;

(2)建立分类模型;

(3)进行分类预测;

(4)输出结果及精度。

3 实验结果及分析

在实验中分别应用了分层流、环状流、泡状流和间歇流四种流型参数，应用独立分量分析法提取出流型的特征参数。选择400个特征参数作为训练样本，同时选取120个样本作为测试样本。支持向量机(SVM)的训练时间为0.35 s，分类时间是0.03 s。正确识别样本数为116个，其中分层流1个、环状流0个、泡状流1个以及间歇流2个。部分数据的实验结果见表1。如果想适合在线识别，则应考虑提高计算机的性能，以降低支持向量机(SVM)的训练时间和测试时间。

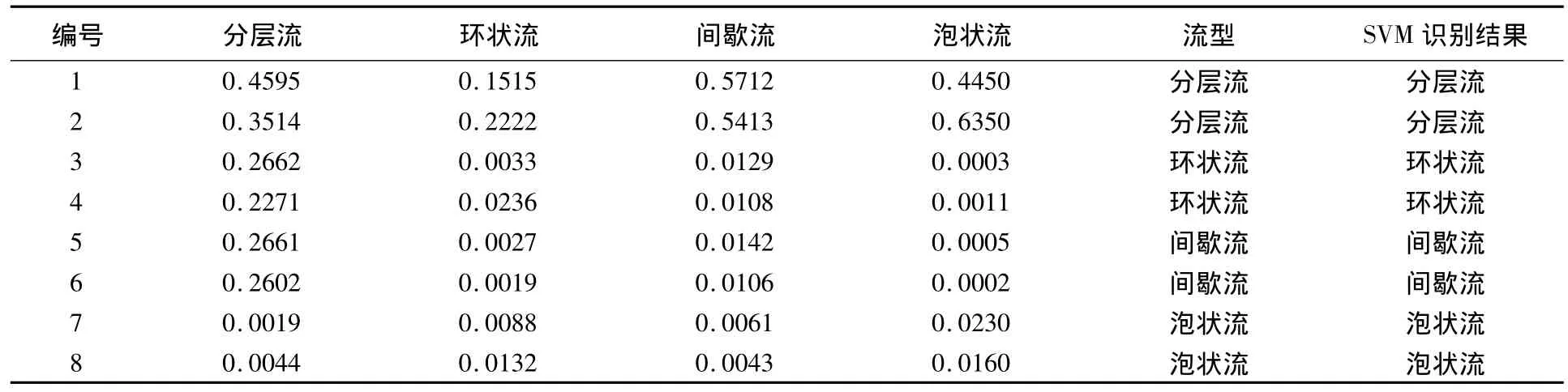
表1 SVM的部分样本

流型误识别的原因可以归结为以下三点:(1)训练样本数目少，可能会由于重要特征点的缺失对识别的准确率产生影响;(2)间歇流参数在较大的范围，易与其他流型产生交叉，因此特征识别率较低;(3)试验中各元件的允许误差叠加产生误差积累，因此流型数据在测试的时候已经收到了污染，使识别结果产生误识别。但是本文的识别率已经可以达到工程要求，具有一定的工程使用价值。

4 结 论

(1)将独立分量分析法应用于流型的特征提取是行之有效的，经过此方法可以得到流型信号的独立特征，由于参数的相关性较小，因此更能准确的表现出流型的原状态。

(2)应用独立分量分析与支持向量机相结合的气液两相流流型识别方法可以避免局部极小问题的出现，此方法可以达到较好的流型识别效果，为流型的识别提供了一种新的、可靠的依据。

［1］周云龙，孙斌，陈飞.气液两相流智能识别理论及方法［M］.北京:科学出版社，2007.

［2］姚福斌，王兆霞.独立分量分析与神经网络在电力系统故障检测中的应用研究［D］.天津:天津理工大学，2008.

［3］朱大奇，朱慧.人工神经网络原理及应用［M］.北京:科学出版社，2006.

［4］张德丰，周品，胡丽华.MATLAB程序设计与典型应用［M］.北京:电子工业出版社，2009.

［5］许建华，张学工，李衍达.支持向量机的新发展［J］.控制与决策，2004，1(5):481-484.

［6］杨福生，洪波.独立分量分析的原理与应用［M］.北京:清华大学出版社，2004.

［7］Lee T W et al.Independent Component Analysis using an extended infomax algorithm for mixed sub-Gaussian and super-Gaussian sources［J］.Neural Computation，1999，11(4):417-441.

［8］杨世锡，焦卫东，吴昭同.基于独立分量分析特征提取的复合神经网络故障诊断法［J］.振动工程学报，2004，14(4):66-70.

［9］申丽言，方斌，沈毅.基于负熵极大的独立分量分析方法［J］.中北大学学报，2005，2(6):396-399.

［10］A.Hyvarinen and E.Oja.A fast fixed-point algorithm for independent component analysis［J］.Neural Computation，1997，9(7):1483-1492.

［11］A.Hyvarinen.Fast and robust fixed-point algorithm for independent component analysis［J］.IEEE Transactions on Neural Network，1999，10(3):626-634.

［12］申丽言，方斌，沈毅.基于负熵极大的独立分量分析方法［J］.中北大学学报，2005，2(6):396-399.

［13］周云龙，孙斌，李洪伟.多相流参数检测理论及其应用［M］.北京:科学出版社，2010.

［14］白鹏，张喜斌，张斌.支持向量机理论及工程应用实例［M］.西安:西安电子科技大学出版社，2008.

［15］张学工.关于统计学习理论与支持向量机［J］.自动化学报，2000，26(1):32-42.

［16］冯元戬，施鹏飞.基于支持向量机的彩色图像人脸检测方法［J］.上海交通大学学报，2003，37(6):947-951.

［17］方瑞明.支持向量机理论及其应用分析［M］.北京:中国电力出版社，2007:160-831.