水面无人艇在风干扰下的操纵性能仿真

马伟佳 庞永杰 杨 衡 吉春正 杜 鑫

（哈尔滨工程大学船舶工程学院1） 哈尔滨 150001） （总参谋部陆航研究所2） 北京 100020）

无人水面艇，简称无人艇或USV（unmanned surface vehicle），其研发晚于陆地机器人、无人机和水下机器人，目前已有多种无人艇应用于科研、军事等领域［1］.国内目前在水面高速无人艇方面的研究还处于起步阶段，在实艇建造方面几乎是空白，与欧美有着非常明显的差距，所以这方面的研究工作对我国跟踪世界潮流，开发实用的高科技海洋军事装备具有重要意义.因为水面高速无人艇艇型以滑行艇为主，所以本文以滑行艇为对象，研究风干扰下滑行艇的操纵性能.

滑行艇因为航速高，其上层建筑受风力的影响较其他船舶尤为显著，研究风干扰下滑行艇的操纵性具有重要的意义.研究滑行艇操纵性可以深入了解样艇的操纵性能，为控制模拟器提供可靠的数学模型，为路径规划提供回转半径、避障距离等重要参数；研究滑行艇特有的回转侧滑、持续内倾、海豚运动等现象，可以对滑行艇的水动力原理有更深刻的认识.

1 滑行艇操纵运动数学模型的建立

1.1 静水中滑行艇操纵运动数学模型

建立随船坐标系，根据质心运动定理和相对于质心运动的动量矩定理来推导得到滑行艇六自由度操纵运动模型［2］.

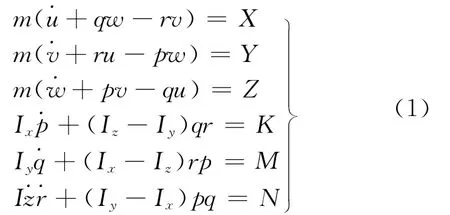
按照MMG分离模型的思想［3］，将惯性类水动力、粘性类水动力、阻尼力、回复力和动升力等代入式（1）中，就得到了静水中滑行艇完整的操纵运动数学模型［4－5］

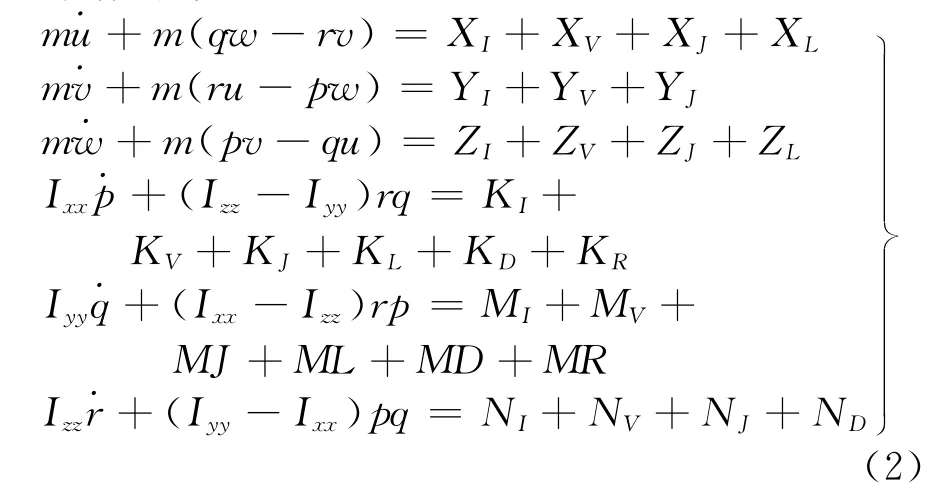
式中：X，Y，Z，K，M，N为船体受力在各方向的分量；I，V，J，L，D，R为惯性力、粘性力、喷水推进力、动升力、阻尼力和回复力.

1.2 风干扰下滑行艇操纵运动数学模型

风作用在船体上层建筑上造成流体动力Fa和力矩Ma，在船舶运动情况下有分量Xa，Ya，Ka，Na.由于船速的影响，船舶遭受的风速和风向与实际风不同.将实际风速、风向称为绝对风速、风向；将船舶受到的风速、风向称为相对风速、风向角.

1.2.1 相对风速和相对风向角的计算

绝对风或真风是在固定地球上的惯性坐标系内观察到的风，绝对风速以UT表示，绝对风向用风向角αT表示，规定北风的αT为0°，东风的αT为90°，依此类推，αT的变化范围为0～360°.相对风是在随动坐标系内观察到的风，相对风速UR和相对风向角（风舷角）αR是在船上用风速计所测量的风速、风向值.αR是UR相对船首的来流角，规定风自右舷吹来时αR＞0°，自左舷吹来时则αR＜0°，故αR的变化范围－180～180°.绝对风速和相对风向间的关系很容易借助图1加以讨论.

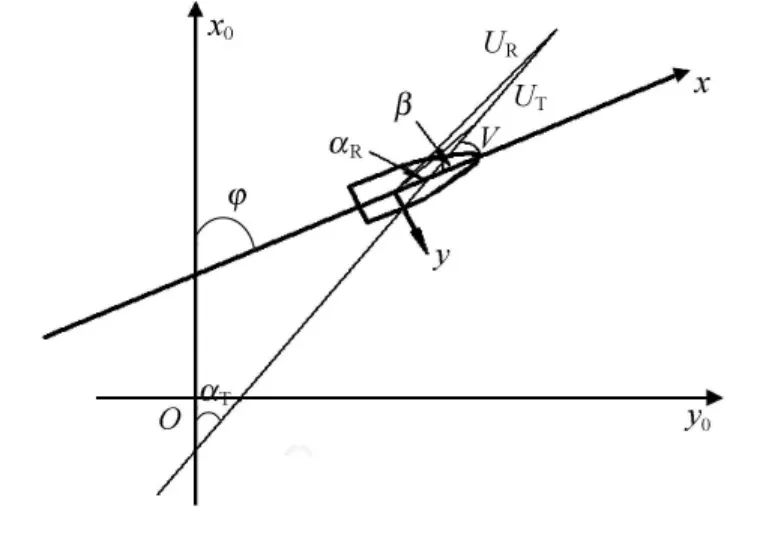
图1 绝对风和相对风示意图

绝对风速UT是船速VT与相对风速UR之间的矢量和，故有

将式（3）投影到随船坐标系x，y轴方向，得

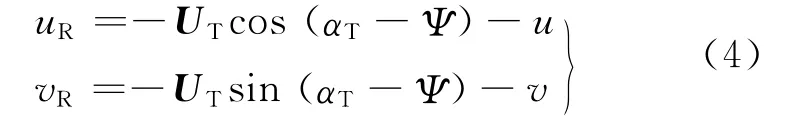
式中：UT为绝对风速的量值；uR，vR为UR的2个分量.风舷角按下面的公式计算

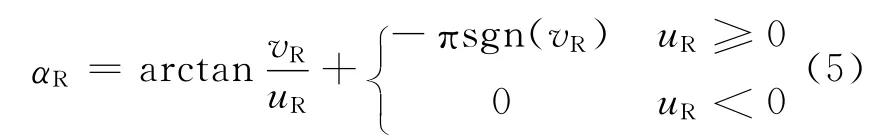
1.2.2 船体上的平均风压力和力矩 作用于船体上的平均风压力和力矩为

式中：ρa为空气密度，kg／m3；Va为相对风速，m／s；Loa为船体总长，m；αa为风压力作用角，rad；ha为风压中心点高度，m；CRa为风压合力系数；Ce为风压作用中心；AT为水线上船体正投影面积，m2；AL为水线以上船体侧投影面积，m2.

1.2.3 风压力系数和风压力的矩系数的估算

通常对所研究的每艘船都进行风洞试验是不切合实际的，人们在进行了大量的风洞试验的基础上，己给出了下列关于风力系数和风压力矩系数的近似估算方法.本文采用汤忠谷的回归公式［6－7］计算风压作用中心Ce、风压力角αa及风压合力系数CRa.

风压作用中心：

式中：CK为侧投影面积形心位置到艏柱的距离.

风压力角：

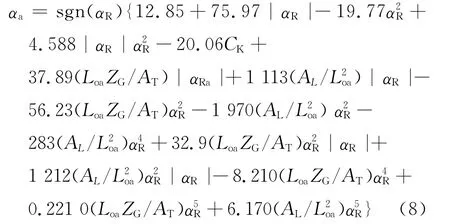
风压合力系数：

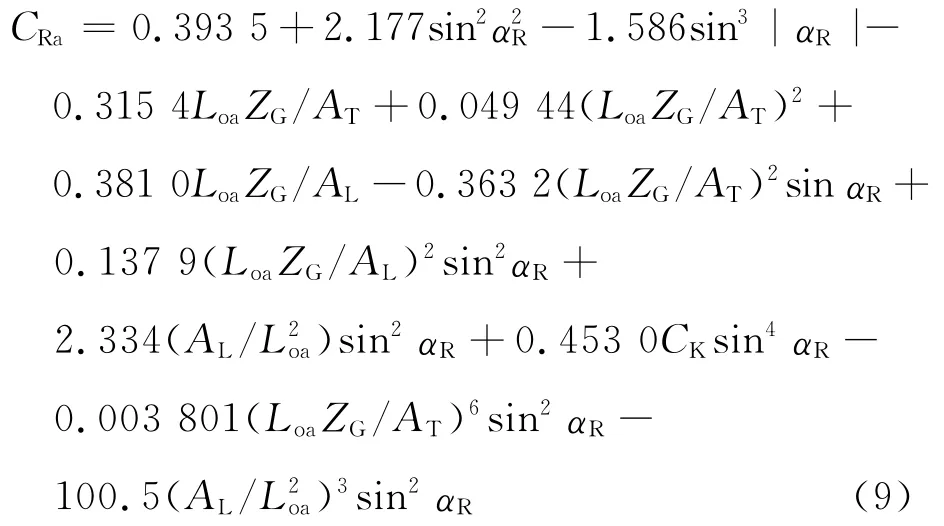
式中：ZG为侧投影面积形心距水线的高度.

2 滑行艇操纵性预报

采用定步长四阶龙格－库塔公式求解操纵运动微分方程，由于滑行艇的运动状态是时变的，所以在过程中求得的参量都是瞬时值［8］.

2.1 静水中滑行艇操纵性预报

通常采用回转机动衡准船舶的回转性能，图2所示为回转机动参量定义.其中DS／L，DT／L，Ad／L及TT／L为无因次定常回转直径、战术直径、纵距和横距.图3所示为u＝3.45m／s，δ＝－15°时数值模拟的回转轨迹.

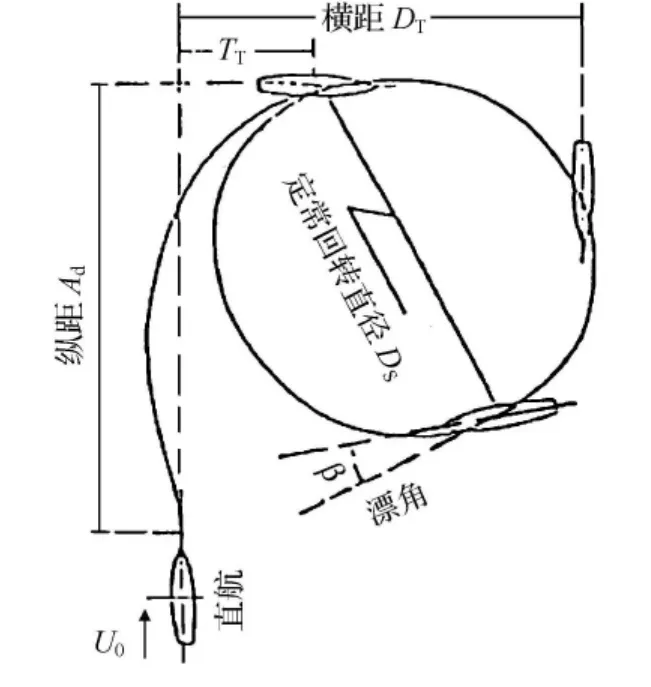
图2 回转机动参量定义

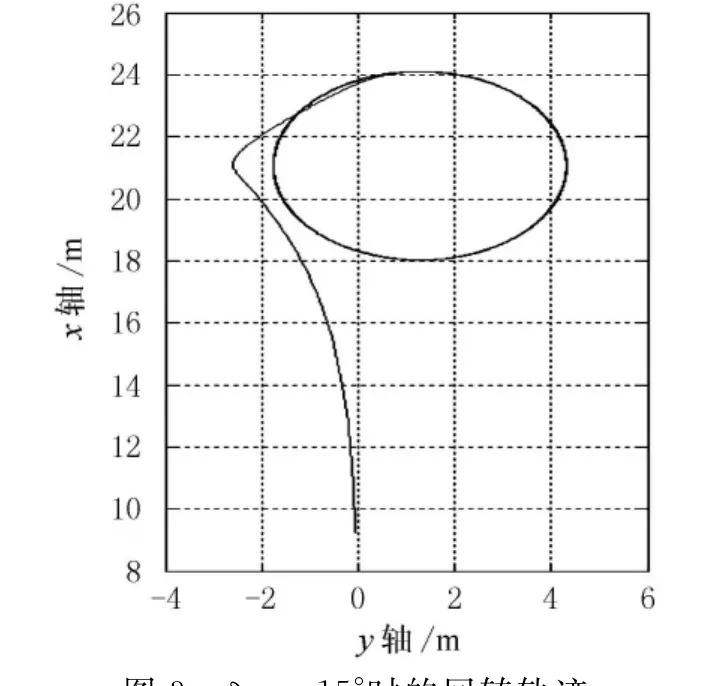
图3 δ＝－15°时的回转轨迹

2.2 风干扰下滑行艇操纵性预报［9－10］

图4 ～7所示为相同风速，不同风向，风干扰下的回转飘移轨迹.

图4 αT＝0时回转飘移轨迹图

图5 αT＝90°时回转飘移轨迹

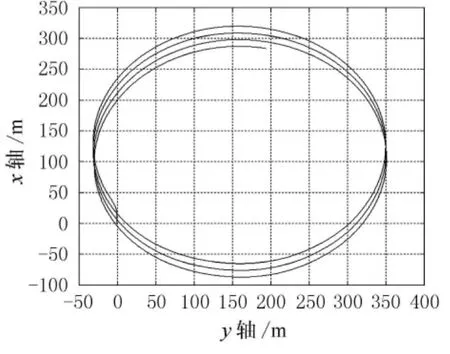
图6 αT＝180°时回转飘移轨迹

图7 αT＝270°时回转飘移轨迹

从图4～7可以看出，在风干扰下滑行艇的回转轨迹将向下风方向飘移.

图8～9所示为相同操舵角，不同风速下的回转飘移轨迹.

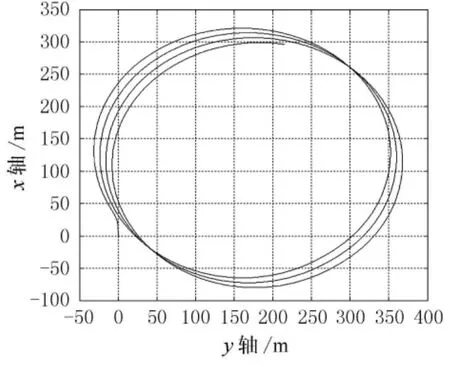
图8 风速u＝1m／s回转飘移轨迹

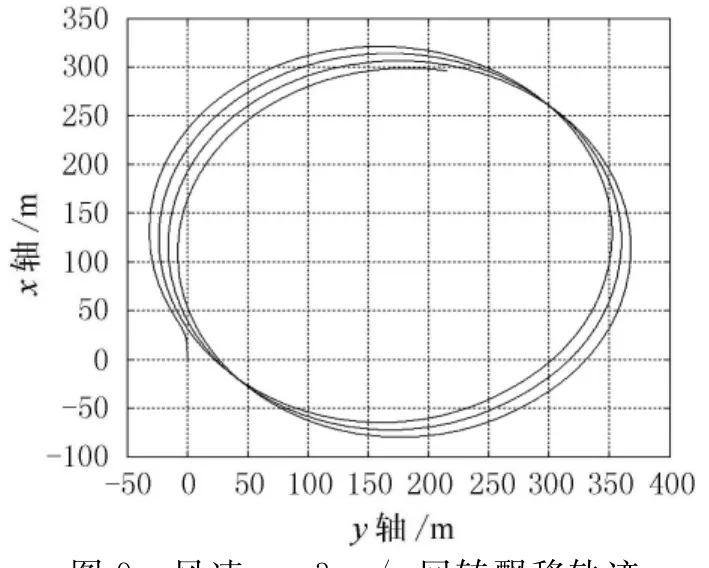
图9 风速u＝3m／s回转飘移轨迹

从图8～9可以看出，随着风速的增大，回转飘移急剧增大.

图10～11所示为相同舵角，不同风速下的横倾角和纵倾角振荡曲线.从中可以看出，随着风速的增大，滑行艇横向和纵向振荡急剧增加.

图10 不同风速横倾角振荡曲线

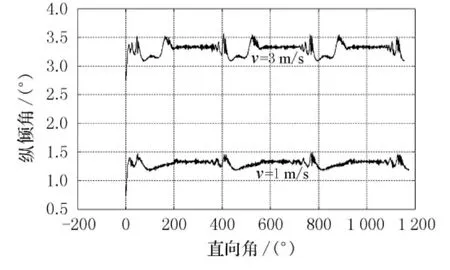
图11 不同风速纵倾角振荡曲线

图12 ～13所示为相同风速，不同操舵角下的回转飘移轨迹，图14～15分别为回转过程中的横倾角振荡曲线和纵倾角振荡曲线.从图中可以看出，大舵角回转时，回转飘移较小，但与此同时，大舵角的横摇和纵摇振荡却比小舵角的为大.

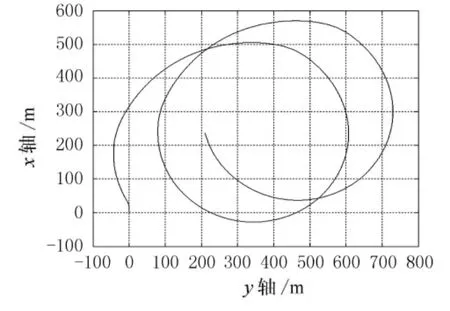
图12 δ＝5°回转飘移轨迹

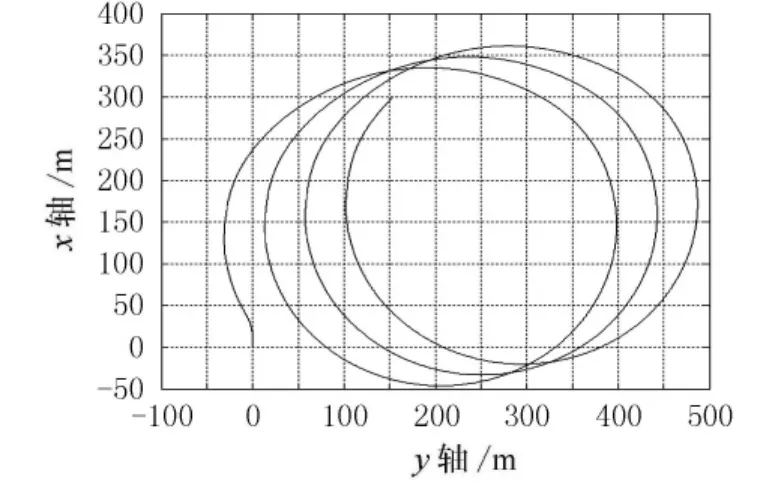
图13 δ＝30°回转飘移轨迹

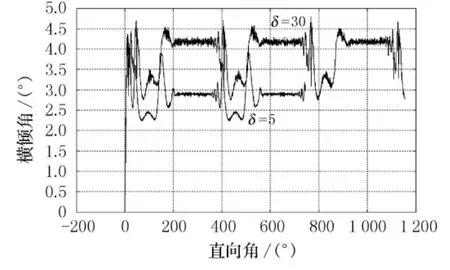
图14 回转中横倾角振荡曲线

图15 回转中纵倾角振荡曲线

3 结 论

综上可知，风干扰下滑行艇的操纵运动有如下特点.

1）滑行艇在风中回转时，风对回转圈的影响很大，艇向下风方向漂移.

2）舵角相同时，漂移量随风力大小而定.风力增大时，漂移量迅速增大.

3）随着风速的增大，滑行艇回转时的横摇和纵摇运动加剧.

4）风速相同，操舵角不同时，操舵角越大，回转飘移越小，而横摇和纵摇运动幅度越大.

对今后这方面研究工作的建议：进一步深入研究风干扰下中滑行艇的操纵性，修正数学模型，完善模拟程序，以便获得更准确的预报结果.

［1］徐玉如，苏玉民，庞永杰.海洋空间智能无人运载器技术发展展望［J］.中国舰船研究，2006（3）：2－4.

［2］范尚雍.船舶操纵性［M］.哈尔滨：哈尔滨工程大学出版社，2003.

［3］董祖舜.快艇动力学［M］.武汉：华中理工大学出版社，1991.

［4］沈定安，孙澄溥.A艇操纵性计算预报［R］.北京：中国船舶科学研究中心，1996.

［5］贾欣乐，杨盐生.船舶运动数学模型［M］.大连：大连海事出版社，1999.

［6］付卫华.船舶操纵运动数值模拟［D］.武汉：武汉理工大学交通学院，2003.

［7］付卫华.风干扰力下的船舶操纵运动［J］.广州航海高等专科学校学报，2004（12）：55－58.

［8］姜建飞.数值分析及其MATLAB实验［M］.北京：科学出版社，2004.

［9］田 超.风浪流作用下船舶操纵运动的仿真计算［D］.武汉：武汉理工大学交通学院，2003.

［10］王化明，邹早建.双桨双舵船舶操纵性预报研究［J］.武汉理工大学学报：交通科学与工程版，2006，30（1）：124－127.