混杂纤维增韧SiC基复合材料的强度分布①
刘善华,张立同,刘永胜,殷小玮,成来飞,李 辉,孟志新
(西北工业大学超高温结构复合材料重点实验室,西安 710072)
混杂纤维增韧SiC基复合材料的强度分布①
刘善华,张立同,刘永胜,殷小玮,成来飞,李 辉,孟志新
(西北工业大学超高温结构复合材料重点实验室,西安 710072)
以采用化学气相渗透法(CVI)制备的SiC纤维和C纤维混杂增韧SiC基复合材料((SiC-C)/SiC)的弯曲强度数据为依据,以Weibull分布为假设,采用图解法结合逐步回归优选法进行参数估计,并采用Kolmogorov-Smirnov法对(SiCC)/SiC复合材料的强度分布进行假设检验。结果表明,(SiC-C)/SiC复合材料的强度统计服从Weibull分布。依据获得Weibull分布函数预测(SiC-C)/SiC的强度值与实验值偏差仅为0.19%,复合材料强度可靠性较好。
(SiC-C)/SiC复合材料;弯曲强度;Weibull分布;Kolmogorov检验
0 引言
连续纤维增强陶瓷基复合材料具有高强度、高硬度、耐高温、低密度等优点,在高温结构材料领域受到了广泛关注。其中,以化学气相沉积法(CVI)制备的C纤维增韧SiC基复合材料(C/SiC)是最具潜力材料之一[1-3]。C/SiC复合材料在由1 000℃的制备温度冷却到室温的过程中,由于纤维与基体热膨胀失配而不可避免地产生基体裂纹,使得复合材料在氧化性气氛中纤维和界面随着材料服役的时间而氧化,影响复合材料的使用寿命[4]。为了减少由于C纤维与基体的热膨胀失配而引起的基体裂纹,采用CVI法制备了3D SiC纤维和C纤维混杂增韧SiC基复合材料((SiCC)/SiC),以减少复合材料的基体微裂纹,提高复合材料的抗氧化性能[5]。
为了证明材料设计的高可靠性,必须给出复合材料的强度可靠性设计方法和数据,进行结构强度可靠性分析。分布函数是可靠性的基本内容,是常用的材料强度可靠性评估的方法之一。本文以制备的(SiCC)/SiC复合材料的实测强度数据为基础,研究了复合材料的强度分布及可靠性。
1 实验过程
1.1 材料制备
混杂纤维预制体采用三维四向编织技术在中国南京玻璃纤维研究设计院制备,两种纤维分别选用日本炭素公司生产的Hi-Nicalon 0.5 K SiC纤维以及日本东丽公司生产的T300 1K炭纤维。混杂纤维预制体是将SiC纤维和C纤维并股编织,预制体的纤维体积分数为40%。采用化学气相渗透法(CVI)分别制备热解炭(PyC)界面相和SiC基体。界面相以C3H6为气源,在900℃、5 MPa条件下沉积144 h;SiC基体以三氯甲基硅烷(MTS,CH3SiCl3)为气源,采用 H2为载气,H2和CH3SiCl3的摩尔比为10∶1,通过鼓泡法将气源反应物引入到反应炉内,在1 000℃、5 MPa下沉积6炉次,每次沉积72 h,此时复合材料并未完全致密化,将未完全致密化的复合材料加工成弯曲强度测试所需的试样尺寸,并将表面抛光以打开未致密的孔隙,再采用上述工艺沉积两炉次SiC基体和涂层,完成整个测试试样的制备过程,最后得到的试样的尺寸为3.5 mm×4 mm×40 mm。
1.2 复合材料的强度测试、假设分布及检验方法
将制备的3D(SiC-C)/SiC复合材料试样在SANS CMT4304试验机上进行室温三点弯曲强度测试。其中,跨距为20 mm ,加载速度为0.15 mm/min。
由于增强体(炭纤维和SiC纤维)和SiC基体均为脆性材料,其强度分布均服从两参数 Weibull分布[6-9]。因此,假设(SiC-C)/SiC复合材料的弯曲强度分布也遵循两参数的Weibull分布:
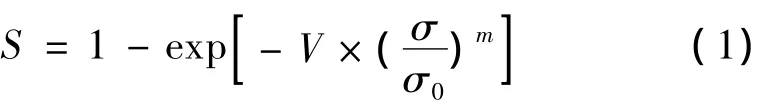
式中S为材料的断裂几率;σ为试样上的作用应力;σ0为归一化常数;V为试样的有效体积,即试样中可能开裂的那部分体积。
对于三点弯曲试样的有效体积计算遵循式(2)[10]:
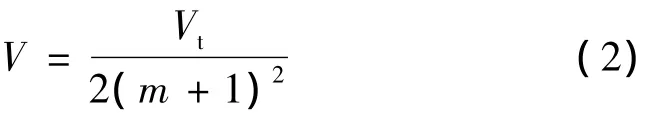
式中Vt为试样的整个体积;m为表征材料均匀性的常数,即Weibull模数。
将式(1)变形并连续2次取常用对数后得到:

从理论上来讲,研究制备材料的分布及可靠性时,样本空间容量越大越好,但在实际应用中出于经济和客观条件的角度考虑,金宗哲[11]和龚江宏[12]指出,对于针对材料配方与工艺条件的单纯实验研究而言,确定Weibull模数所需的最小样本空间容量为16。徐永东[13]等指出,对Weibull分布模型的参数进行参数估计时,样本容量一般不少于20。本文采集了20个样本数据。
将测得的强度数据由小到大排列,然后采用图解法结合逐步回归优选法求解式(3)中的参数因子,最后采用Kolmogorov-Smirnov检验法,检验其是否服从Weibull分布。
2 结果与讨论
2.1 强度分布
采用三点弯曲法测得的(SiC-C)/SiC复合材料的平均强度为530 MPa,将测得的强度数据由小到大排列,然后采用图解法结合逐步回归优选法求解式(3)中的参数,结果列于表1。由文献[10]得知,Weibull分布的强度断裂几率S可由式(4)表示:

式中N为实验的总次数;n代表第n次实验,n≤N。
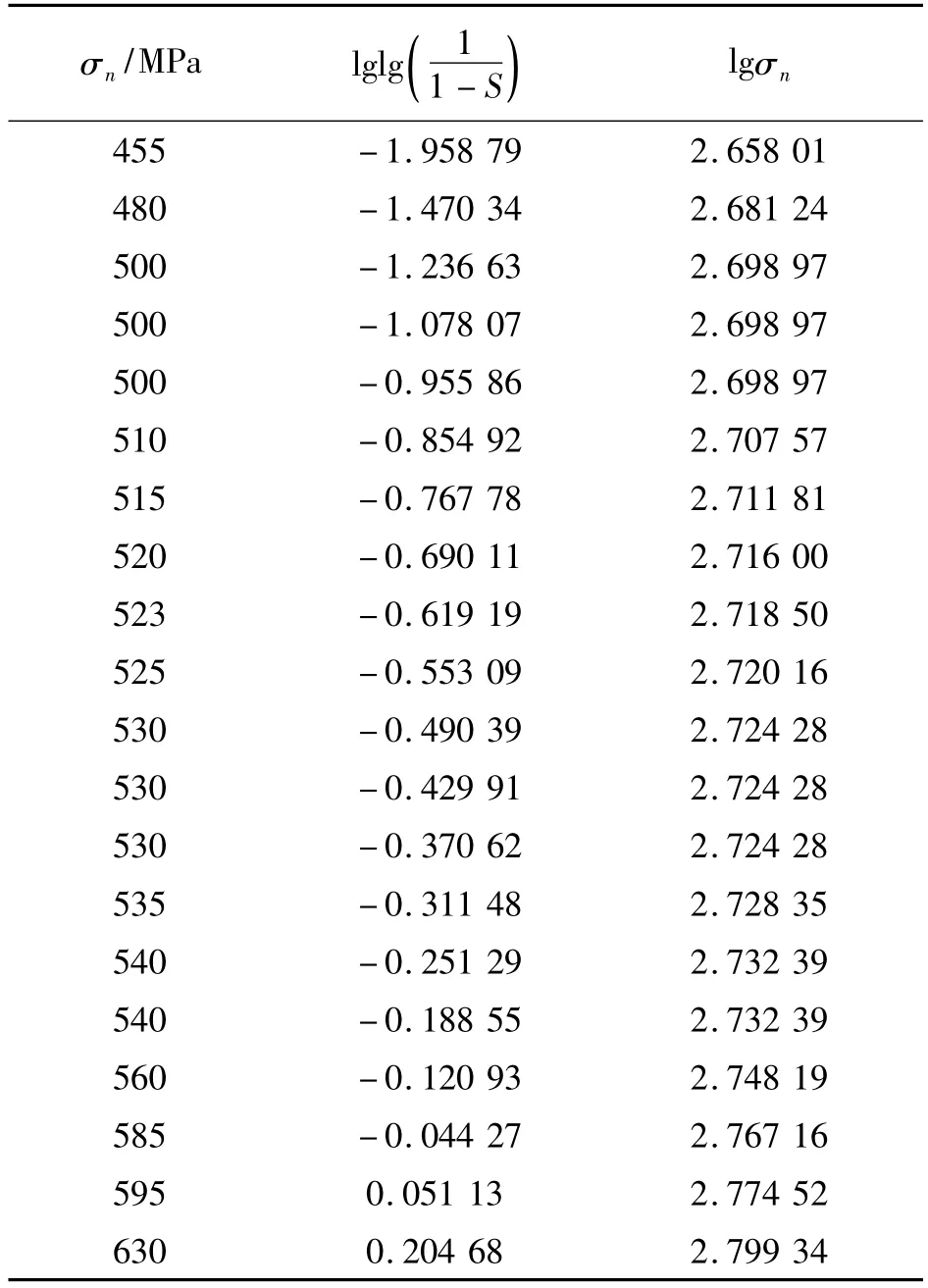
表1 图表法计算(SiC-C)/SiC复合材料Weibull参数所需基本数据Table 1 Basic calculation to Weibull parameter estimation by graphical method for(SiC-C)/SiC composite

根据式(5)可得,(SiC-C)/SiC复合材料的m及σ0分别为15.8和547,最后得到(SiC-C)/SiC复合材料的弯曲强度分布函数为
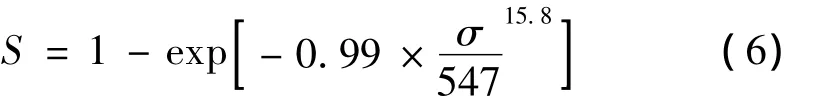
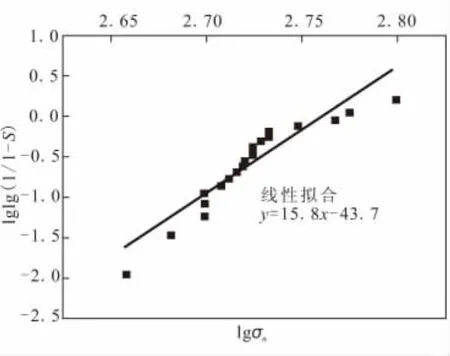
图1 求解(SiC-C)/SiC复合材料Weibull参数的与lgσ 线性拟合图nFig.1 (SiC-C)/SiC linear fitting of lglg)to lgσnin parameter evaluation
Weibull模数可用来表征材料强度数据的分散性,模数m在2~5之间时,表示材料的强度分散性较大,Weibull模数大于5时,材料的分散度较小[14]。本文计算得到(SiC-C)/SiC复合材料的Weibull模数分别达到15.8,说明复合材料的强度分散性均较小。
2.2 假设检验
采用Kolmogorov-Smirnov检验法可检验强度统计是否服从Weibull分布[15]。假定(SiC-C)/SiC复合材料的单个样本空间的强度值n1、n2、…、n20是来自分布F(n)的1组样本,假定其服从某种理论分布,即检验假设:H0:F(n)=F0(n)↔H1:F(n)≠F0(n)。Kolmogorov-Smirnov检验采用统计量Dn=sup|Fn(n)-F0(n)|,指出给定水平 α,可得到临界值Dn,α,使得P{Dn>Dn,α}= α,如果样本观察值Dn<Dn,α,则接受假设H0∶F(n)=F0(n),反之则否定。根据上述假设强度分布,采用 Kolmogorov-Smirnov法检验得到表2。
取 α=0.05,查 Kolmogorov-Smirnov检验的临界值Dn,α表得:D20,0.05=0.294 03,(SiC-C)/SiC 复合材料的最大Dn=0.223 00,小于 0.294 03,接受检验。(SiC-C)/SiC复合材料的强度统计服从求解的Weibull分布。
2.3 强度预测
根据上述检验3D(SiC-C)/SiC复合材料室温弯曲强度分布,可采用Weibull分布函数表征 ,由式(1)可得分布函数为
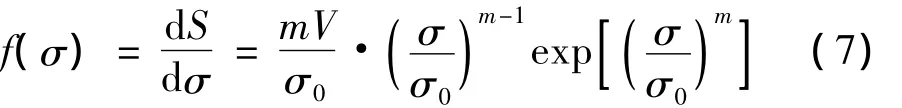
强度均值为
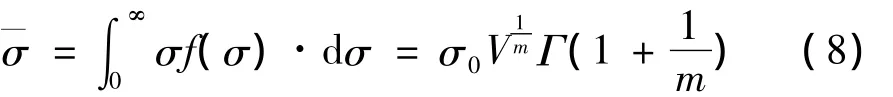
将σ0、V、m代入式(8),计算得到复合材料强度均值为529 MPa。显然,根据Weibull分布函数计算所得的复合材料强度值略低于实测值530 MPa,两者的偏差仅为0.19%。从可靠性设计角度讲,该分布的预测值趋于安全。因此,采用两参数 Weibull分布能表征该3D(SiC-C)/SiC复合材料室温弯曲强度分布。
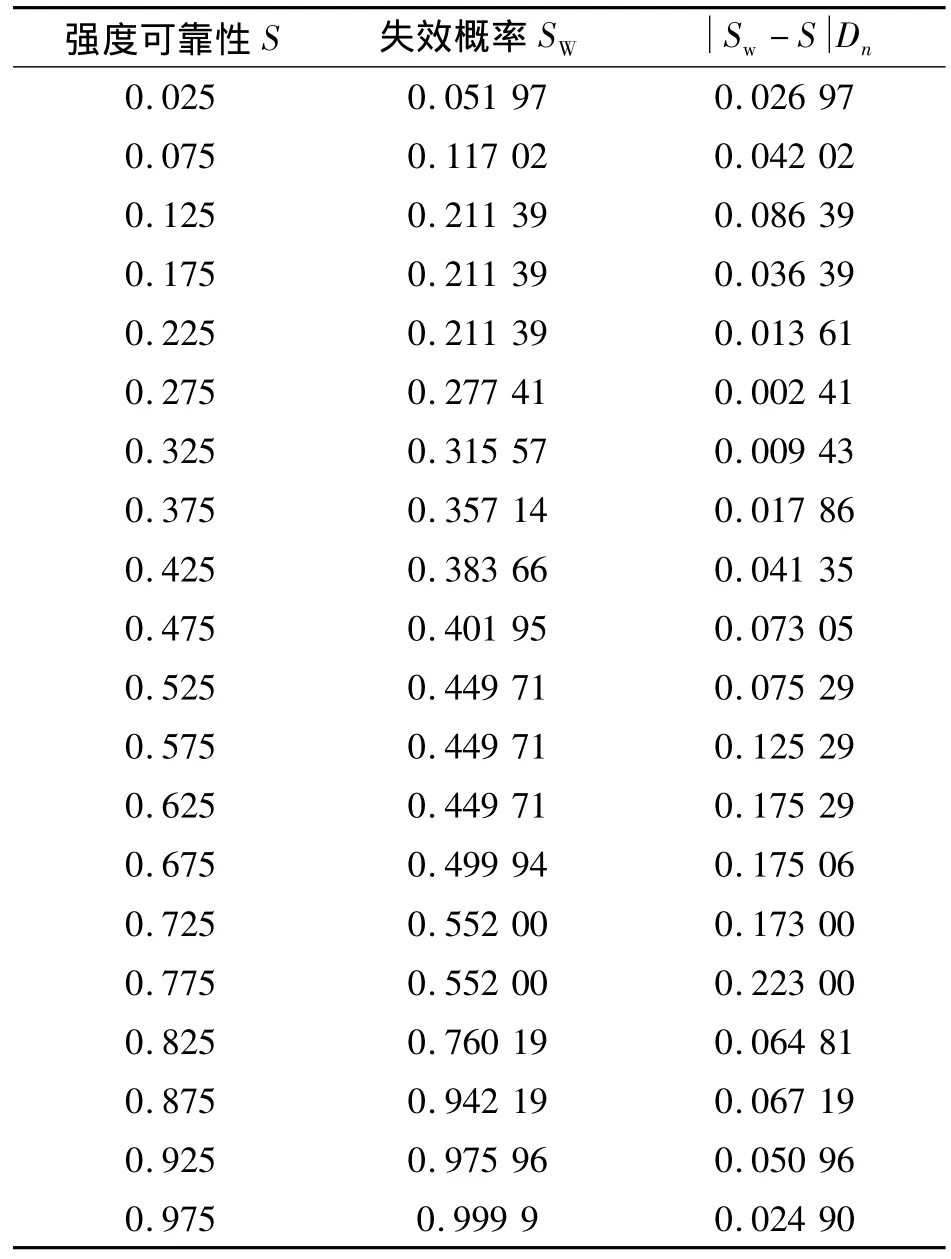
表2 (SiC-C)/SiC Kolmogorov-Smirnov检验过程数据Table 2 Data of Kolmogorov-Smirnov test for(SiC-C)/SiC composite
3 结论
以Weibull分布为假设分布,采用图解法结合逐步回归优选法进行参数估计,利用Kolmogorov-Smirnov检验假设的3D(SiC-C)/SiC复合材料室温三点弯曲强度分布。结果表明,采用 Kolmogorov-Smirnov法,证实了3D(SiC-C)/SiC复合材料弯曲强度分布服从Weibull分布。依据满足检验的Weibull分布函数,预测复合材料的弯曲强度值与实际测得的强度值的偏差仅为0.19%,复合材料的可靠性较高。
[1]张立同,成来飞,徐永东.新型炭化硅陶瓷基复合材料的研究进展[J].航空制造技术,2003,1:24-32.
[2]Evens A G,Zok F W.The physics and mechanics of fibre-reinforced brittle matrix composites[J].J.Mater.Sci.,1994,29(15):3857-3896.
[3]Naslain R R,Pailler R,Bourrat X.Synthesis of highly tailored ceramic matrix composites by pressure-pulsed CVI[J].Solid State Ionics,2001,141-142:541-548.
[4]Sullivan R M.A model for the oxidation of carbon silicon carbide composite structures[J].Carbon,2005,43:275-285.
[5]Liu Shan-hua,Zhang Li-tong,Yin Xiao-wei,et al.Microstructure and mechanical properties of SiC and carbon hybrid fiber reinforced SiC matrix composite[J].Int.J.Appl.Ceram.Technol.,2011,8(2):308-316.
[6]Fok S L,Mitchell B C,Smart B J,et a1.A numerical study on the application of the Weibull theory to brittle materials[J].Eng.Fract.Mech,2001,68(10):1171-1179.
[7]Konstantinos G D,Marc S,Constantina F.Mechanical properties of alumina NextelTM720 fibres at room and elevated temperatures:tensile bundle testing[J].Mater.Sci.Eng.A,2003,349(1-2):63-72.
[8]Pickering K L,Murray T L.Weak link scaling analysis of high-strength carbon fibre[J].Composites,Part A,1999,30(8):1017-1021.
[9]Andersons J,Joffe R,Hojo M,et al.Glass fibre strength distribution determined by common experimental methods[J].Compos.Sci.Technol.,2002,62(1):131-145.
[10]关振铎,张中太,焦金生.无机材料物理性能[M].第1版.北京:清华大学出版社,1992:33-35.
[11]金宗哲,马眷荣,汪林生,等.结构陶瓷弯曲强度的weibull统计实验研究[J].硅酸盐学报,1990,18(2):130-136.
[12]龚江宏.陶瓷材料断裂力学[M].第1版.北京:清华大学出版社,2005:174-175.
[13]X Yong-dong,C Lai-fei ,Z Lit-ong,et al.Optimization of sample number for Weibull function of brittle materials strength[J].Ceram.Int,2001,27(2):239-241.
[14]Antbn N,Velaseo F,Gordo E,et al.Statistical approach to mechanical behavior of ceramic matrix composite based on Portland clinker[J].Ceram.Int.,2001,27(4):391-399.
[15]吴喜之,王兆军.非参数统计方法[M].第1版.北京:高等教育出版社,1996:151-167.
Strength distribution of hybrid fibers reinforced SiC matrix composite
LIU Shan-hua,ZHANG Li-tong,LIU Yong-sheng,YIN Xiao-wei,CHEN Lai-fei,LI Hui,MEN Zhi-xin
(Key Laboratory of Thermo-Structure Composite Materials,Northwestern Polytechnical University,Xi'an 710072,China)
Based on the flexural strength of 3D(SiC-C)/SiC composite in which SiC matrix was reinforced by hybrid SiC fiber and carbon fiber fabricated by chemical vapor deposition process(CVI),assumed by the Weibull distribution,the strength distribution of(SiC-C)/SiC composite was studied by a graphical method and stepwise regression method to optimize the estimated parameters,The Kolmogorov-Smirnov test method was used to examine the supposed distribution.The results show that the strength of(SiCC)/SiC obeys Weibull distribution.The deviation was only 0.19%between the test value and predicated date obtained by function of Weibull distribution,which indicate that the composite possesses perfect strength reliability.
(SiC-C)/SiC composite;flexural strength;weibull distribution;Kolmogorov-Smirnov test
V258
A
1006-2793(2012)03-0410-04
2011-12-20;
2012-01-05。
国家自然基金项目(50972119,50902112)。
刘善华(1984—),男,博士生,研究方向为陶瓷基复合材料。E-mail:shanhauliu@yahoo.com
刘永胜,男,副教授。E-mail:yongshengliu@nwpu.edu.cn
(编辑:薛永利)

