基于四元数小波混合统计模型的图像去噪
殷 明, 刘 卫
(合肥工业大学数学学院,安徽 合肥 230009)
传统的图像去噪方法主要有空域低通滤波、统计滤波(如维纳滤波)及频域滤波等,虽然这些方法对噪声有一定的抑制效果,但是损失了许多图像的细节信息,会造成图像模糊,产生振铃现象。小波变换在时域和频域同时具有良好的局部化性质,不仅可将图像的结构和纹理分别表现在不同分辨率层次上,而且具有检测边沿的能力。因此,利用小波变换在去除噪声时,并且能够较好地保持图像的细节,可提取并保存对视觉起主要作用的边缘信息,成为常用的去噪方法。基于小波分析的去噪方法最早是由 Mallat于1992年提出的基于模极大值的图像去噪法[1],Donoho在1994年提出采取全局阈值的小波系数萎缩方法[2],1998年 Crouse等人提出小波域的隐马尔科夫树模型HMT[3],及后来Sendur等人考虑了小波系数上下级的相关性,提出BiShrink[4]和Local—BiShrink[5]方法,2005年,Cho等人提出了基于广义高斯分布的统计去噪法[6],广义高斯分布(GGD)是一类以Laplacian分布和Gaussian分布为特例,以δ函数和均匀分布为极限形式的对称分布。常用的小波有离散小波变换(DWT)、复小波(CWT)及脊波(Ridgelet)等。
四元数小波变换是实小波、四元数理论及二维希尔伯特变换相结合的产物,它是一种新的多尺度分析图像处理工具,具有近似平移不变性,它克服了以往实小波的两个不足[7-8],第一,实离散小波变换(DWT)中,当图像(信号)微小平移后,图像的平滑和边缘区域的特征会产生很大的变化, 形成边缘处的模糊;第二,用相位表示图像的局部信息。双树复小波虽然克服了第1个问题,但是它只有一个幅角,在表示二维图像特征时会产生信号相位歧义。
广义高斯分布是目前采用的先验模型,虽然在尺度内可以很好的模拟小波系数的概率分布,但它完全忽略了小波系数尺度间的相关性;二元非高斯分布模型由一个实参和两个变元构成,可以很好地体现小波系数尺度间的相关性,但无法体现尺度内的小波系数之间的联系。本文提出一种混合统计模型,该模型结合尺度内和尺度间两个模型的特点,先用非高斯分布模型模拟尺度间系数分布,将小波系数划分为两类:重要系数和不重要系数;再用广义高斯分布模拟尺度内系数,运用最小均方误差估计(MMSE)从噪声图中的小波系数恢复原图的小波系数。然后将该混合模型与四元数小波相结合,将其应用于图像去噪中。需要说明的是,文中所提出的模型,去噪同时相当于对图像进行压缩,记本文中的压缩比为小波去噪的压缩比,并用零系数所占的比例来刻画。实验表明:该方法不仅取得了很好的去噪效果,图像的压缩比也较高。
1 四元数小波变换
1.1 四元数解析信号

定义 1 设 f( x, y)使一个实二维信号,则四元数解析信号可定义[9]为为信号 f( x, y)沿x轴和 y轴 及沿x, y轴的Hilbert变换。
1.2 二维四元数小波变换

则可以得到四元数小波的尺度函数及水平、垂直、对角方向的小波函数的具体形式如下
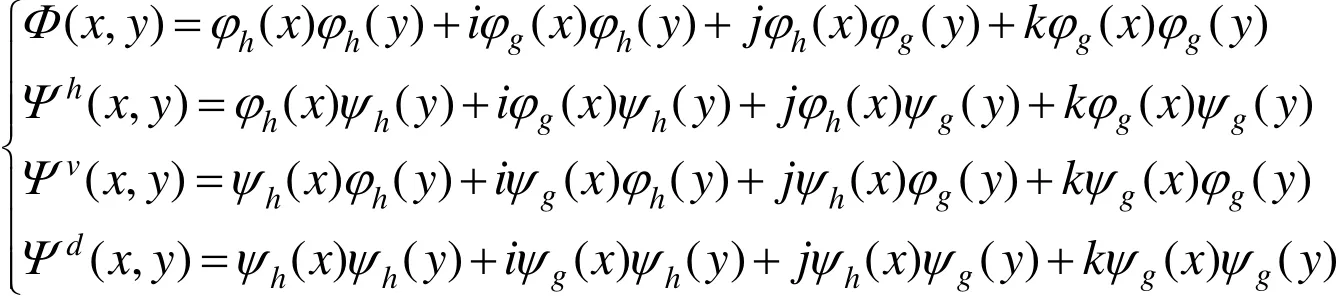
四元数小波变换采用了 4个实离散小波变换(DWT),第1个实离散小波对应四元数小波的实部,第2,3及4个实离散小波是由第1个实离散小波经Hilbert变换所得到,分别对应四元数小波的3个虚部。
2 混合统计模型
2.1 尺度间模型
在小波变换域上不同尺度间的小波系数存在一定的相关性,在Lewis和Knowles零树编码思想中[10],提出这样一个假设:如果在某一尺度上的小波系数(父系数)较大(小),那么在其临近尺度上同一个空间位置上的小波系数(子系数)往往也会比较大(小)。于是可以将小波系数划分为两类:重要系数和不重要系数。具体算法为:设定一个阈值T,当父系数大于T时,那么子系数为重要系数,否则子系数为不重要系数。由这种思想使得零树编码得到了较高的压缩比。但实际图像进行小波分解后,仅比较父系数就得出子系数的分类,会有很大的误差,阈值T也不容易确定。于是我们提出用非高斯分布来模拟尺度间的父子小波系数。

它是一个对称的概率密度函数,其最重要的特征就是可以很好的体现m1和m2的相关特性。它可以很好的体现小波系数上下层之间的关系。其中a是一个自由参数,在图像处理过程中可以灵活的选取a的大小。文献[11]直接将a取为 4来进行后续工作,但在多次实验后可以发现a大小在3附近。本文将a取为3,定义函数
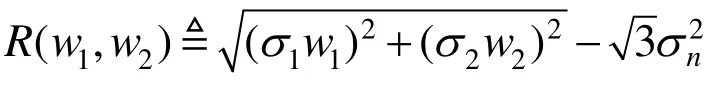
分类准则的证明类似于文献[11]。由分类准则可以得到两类小波系数,由于小波系数具有稀疏特性,从而直接令不重要的小波系数为零,对那些重要的小波系数再在下面的尺度内模型上运用MMSE估计原图像的小波系数。
2.2 尺度内模型
Mihcak等人提出LAWML和LAWMAP方法[12],由于采用了局部适应性很强的系数模型,得到了较好的去噪效果。但是由于过多的保留了小波系数,从而重建的图像毛刺现象很严重,也不利于压缩。本文由于考虑了尺度间和尺度内的关系,可以很好的解决上述问题。
LAWMAP是以LAWML为基础提出来的,本文只采用LAWML方法。LAWML方法是以双随即过程为小波系数模型。此模型将小波系数看成互相独立的高斯变量,若已知的话,用MMSE来估计小波系数为


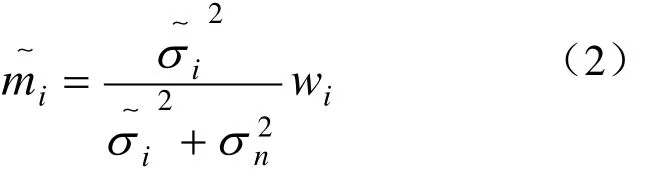
从上式可以看出,LAWML方法实际上就是比例萎缩法。对每层的重要小波系数用式(2)即可得到原图像的小波系数的估计。
3 图像去噪的算法步骤

下面给出算法步骤:
Step 1 对含噪图像进行 5层四元数小波(QWT)分解;
Step 2 用式(3)估计噪声标准差,用式(1)估计小波系数方差;
Step 3 用分类准则对小波系数进行分类,对不重要的小波系数直接置为零,对重要的小波系数用式(2)估计原图像小波系数;
Step 4 将估计得到的小波系数进行四元数小波逆变换(IQWT),得到降噪图像。
4 仿真实验与分析
在仿真实验中,对512×512的Lena和Barbara图像进行测试,加入均值为零、方差为 σn2的高斯白噪声。将本文的去噪方法与选用 Donoho’s HT方法[13](db8小波)进行硬阈值,Mihcak[12]等人提出LAWML(5×5)以及Bayes风险最小的阈值法(BayesShrink)的去噪方法进行比较。然后运用去噪后的图像的峰值信噪比(PSNR)和视觉效果来评价本文的方法。其中峰值信噪比定义为其中,X、Y分别为原始图像和去噪后的图像,N2为图像大小。
下面我们给出去噪结果的PSNR、效果图及零系数所占比例。
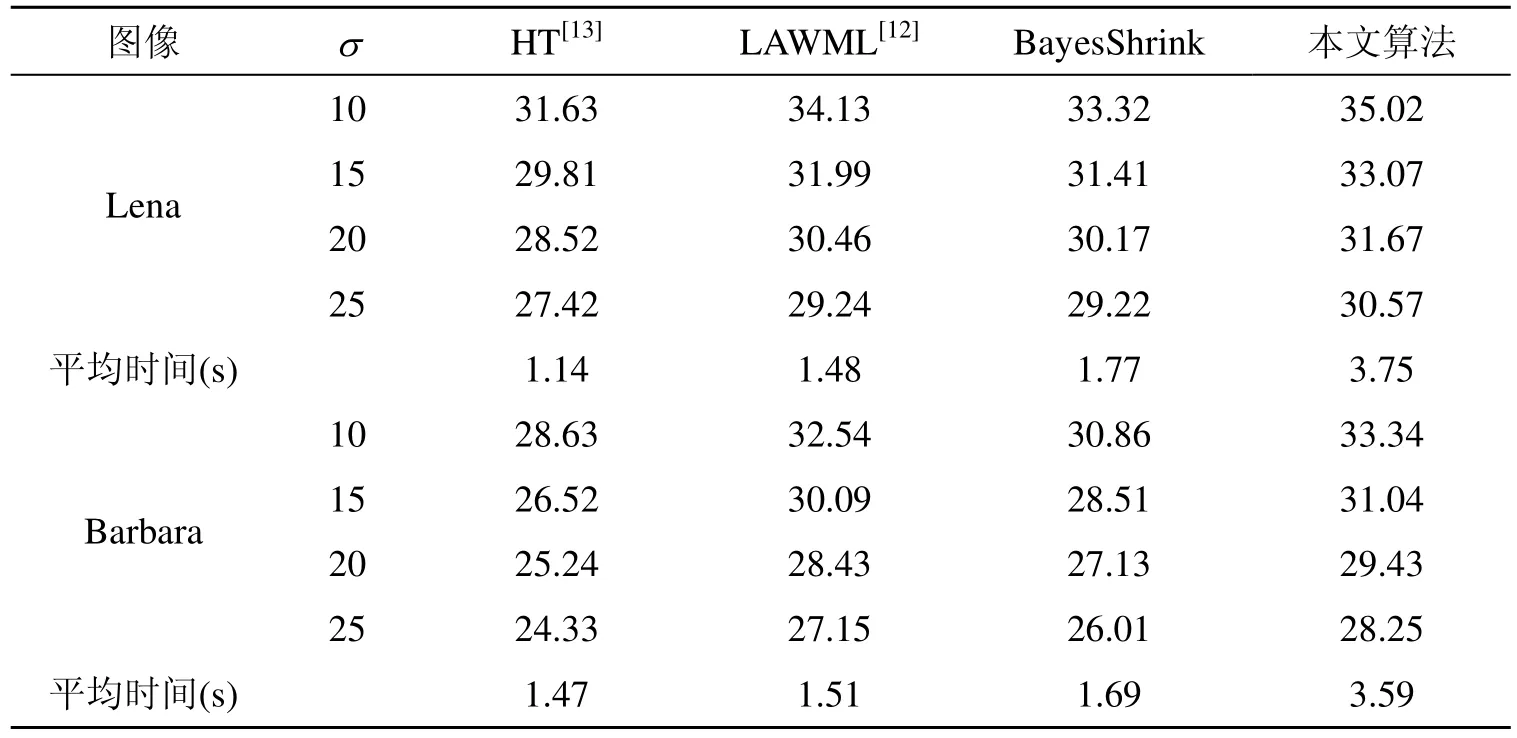
表1 含噪图像去噪后的峰值信噪比及时间

图1 噪声标准差σn=25的Lena图像的各种算法去噪图像

图2 噪声标准差σn=25的Barbara各种算法去噪图像

图3 σn=25的 Lena 图像去噪后局部放大图

表2 本文方法去噪后小波系数中零系数占的比例
从实验数据及效果图可以看出,本文提出的基于四元数小波的混合统计模型图像去噪方法比 Donoho’s HT 方法[13](db8小波)硬阈值和BayesShrink去噪效果有明显的优势,在峰值信噪比上取得了较大的提高,从图3可以看出:本文去噪方法保留了图像大部分细节信息,图像更光滑,视觉效果更好;与Mihcak等人[12]提出的LAWML也有不少改善,不仅获得了比上述这些方法有更好的峰值信噪比,而且从表2可以看出,由于LAWML方法去噪后的零系数很少,而本文的去噪方法零系数占了相当大的比例,去噪后的压缩比与经典的比例萎缩法有了较大提高。
5 结 论
本文提出了基于四元数小波的混合统计模型图像去噪,利用小波系数尺度间和尺度内的相关性,分类出重要系数和不重要系数,再用比例萎缩法估计出原图像的小波系数。无论在峰值信噪比上还是在视觉效果上都优于许多经典的去噪算法,并且取得了较高的压缩比。虽然计算时间上稍长些,但是大多数情况下不会影响其在实际中的应用。
[1]Mallat S, Hwang W L. Singularity detection and processing with wavelets [J]. IEEE Transactions on Information Theory, 1992, 38(2): 617-643.
[2]Donoho D L. Denoising by soft-thresholding [J]. IEEE Transactions on Information Theory, 1995, 41(3):613-627.
[3]Crouse M S, Nowak R D, Baraniuk R G. Waveletbased statistical signal processing using hidden markov models [J]. IEEE Transactions on Signal Processing 1998, 46(4): 886-902.
[4]Sender, Ivan W, Selesnick. Bivariate shrinkage functions for wavelet-based denoising exploiting interscale dependency [J]. IEEE Transactions on Signal Processing, 2002, 20(11): 2744-2756.
[5]Levent S, Ivan W S. Bivariate shrinkage with local variance estimation [J]. IEEE Signal Processing Letters, 2002, 9(12): 438-441.
[6]Cho D, Bui T D. Multivariate statistical modeling for image denoising using wavelet transforms [J]. IEEE Transactions on Signal Processing Image Communication, 2005, 20(1): 77-89.
[7]Corrochano E B. The theory and use of quaternion wavelet transform [J]. The Journal of Mathematical Imaging and Vision, 2006, 24(1): 19-35.
[8]Corrochano E B. Multi-resolution image analysis using the quaternion wavelet transform [J]. The Journal of Numerical Algorithms, 2005, 39(1): 35-55.
[9]Bulow T. Hypercomplex spectral signal represemtation for the processing and analysis of images [D]. 1999.
[10]Lewis A S, Knowles G. Image compressing using the 2-D wavelet transform [J]. IEEE Transactions on Image Processing, 1992, 1(2): 224-250.
[11]易 翔, 王蔚然. 一种概率自适应图像去噪模型[J].电子学报, 2005, 33(1): 63-66.
[12]Mihcak M K, Kozintsev I, Ramchandran K.Low-complexity image denoising based on statistical modeling of wavelet coefcients [J]. IEEE Signal Processing Letters, 1999, 6(12): 300-303.
[13]Donoho D, Johnstone I. Ideal spatial adaptation via wavelet shrinkage [J]. Biometrika, 1994, 81(9):425-455.

