NURBS曲面光顺方法综述

尹小奎， 李奇敏， 叶仲泉， 蒋恒恒

（1.重庆大学数学与统计学院，重庆 400044；2. 重庆大学机械工程学院，重庆 400044）

在飞机、汽车、船舶以及家用电器等的计算机辅助设计中经常遇到许多由二次曲线弧与二次曲面所表示的形状，为描述这些形状，Gordon和Riesenfeld于1974年提出了B样条曲线曲面，较成功地解决了曲线曲面局部控制问题，并在参数连续性基础上解决了连接问题。由于B样条方法不能精确表示圆锥及初等解析曲面，Verspril于1975年首次提出有理B样条方法。后来由于Pieg和Tille等的工作，终于使非均匀有理B样条(NURBS)方法成为现代曲面造型中最为广泛流行的技术。随着生产的发展，人们对于产品的外形也有了要求，其中之一就是外形的光顺性。如果曲线、曲面不光顺，就不能满足产品的设计要求，也不便于加工。因此，NURBS曲线、曲面的光顺处理就成为 CAD/CAM 中非常重要的一个问题。

由于曲线、曲面的光顺性涉及几何外形的美观性，难免受到主观因素的影响，而且在不同的实际问题中，对其的要求也不同。对于判断曲线、曲面的光顺性的光顺准则一般可分为两类：一类是整体光顺准则，如在能量法中采用的光顺准则为“弹性模板应变能较小”，而最小二乘法采用的是“剪力跃度较小”。另一类是局部光顺准则，如根据曲面上的关键曲线（如 u，v方向的参数线，或者曲面与平行于坐标平面的一系列平面的截面线等）是否光顺，以及曲面的曲率（主曲率、高斯曲率、平均曲率等）的变化是否均匀等来判定。浙江大学的马利庄和石教英给出了如下的曲面光顺准则[1]：

关键曲线（如飞机或船舶曲面的骨架线）光顺；

网格线无多余拐点（或平点）及变挠点；

主曲率（低次曲面）在节点处的跃度和足够小；

弹性薄板的应变能较小；

高斯曲率变化均匀。

此外，在汽车工业中，还常用平行光照射到车身上来检查曲面的光顺性。对于带有特征的曲线、曲面，如在复杂产品设计中需要设计出的曲面带有边界轮廓，表面棱线等特征，这些带有关键信息的特征应该在光顺过程中被保留。本文在总结了曲面光顺中的几种常用方法的特点，针对这些方法在光顺中保特征性的不足，结合各向异性小波在表达高维信息的优势，提出将其融入曲面的多分辨率分析，以达到保特征的目的。

1 基于能量的曲面光顺方法

1.1 最小二乘法

上世纪 60年代初，最小二乘法曾是最有影响的一种光顺方法。最小二乘法将样条的剪力跃度平方和作为目标函数进行优化，使其达到最小值来实现光顺，因而可以使样条在光顺后的曲率变化比较均匀。朱心雄等人将其推广到对空间参数三次B样条曲线的光顺[2]。此外，用拉格朗日乘数法对带约束的光顺目标函数进行优化设计，可以得到保形的光顺逼近曲线[3]。但是最小二乘法是整体光顺法，需要将曲线、曲面的所有控制顶点作为未知量，计算量大、计算速度慢。

1.2 能量法

能量法的基本思想是将光顺问题转化为包含型值点偏差和光顺两部分加权平均的目标函数的极小化问题。能量法的关键是能量函数（光顺准则）E(V)的选取，通常是通过对弹性薄板应变能进行简化或近似得到的。在选取能量函数时，需要考虑其是否具有明确的物理意义或几何意义，以及实际问题中对光顺性的具体要求等。如针对参数曲面，Lott和Pullin[4]提出的一种薄板应变能的简化形为曲面的主曲率）对曲面光顺时会使曲面趋于平坦。Moreton[5]提出的采用

能量法具有很强的物理背景，光顺效果好，但计算量大，计算速度慢。对此，穆国旺等[6]提出分片能量法，大大地减少了存储量和计算量。此外，将能量法与选点法相结合进行曲线曲面光顺[7]，一次性修改所有对坏点有影响的控制顶点，减少了计算量，也使得曲线曲面的形状改变尽可能小。将能量法与最小二乘法相结合[8]，在对 B样条曲线光顺时可以使曲线的光顺性及逼近性提高，使曲线的曲率变化更加均匀。

1.3 选点修改法

选点修改法是一种局部光顺法，适用于少数型值点处不光顺的情况。该方法充分利用NURBS曲面可以通过调整控制顶点来达到修改曲面形状的特点，逐次找出不符合光顺准则的型值点（称为“坏点”），并依次对“坏点”进行修改。特别是对于曲面上“坏点”的选取较为复杂，需借助曲面的等曲率线、等照度线或反射线等曲面分析工具，结合交互的方法来判断曲面在哪些区域不光顺。目前，“坏点”的修改方法主要有Kejellander方法和Farin的节点删除与插入法、圆率法、基样条方法等。选点修改法的优点是计算速度快，修改能力强，具有局部性。但当连续出现多个坏点时，光顺效果往往比较差。胡海艳等[9]应用广义逆矩阵使节点消去，并通过升阶和最小二乘逼近等步骤得到光顺的目标曲线。该方法减少了Farin光顺方法的计算量，但不能直接用于样条曲面的光顺。将选点修改法与小波多分辨率分析方法结合，Martin Bertram提出的单节点小波[10]，删除“坏点”后根据小波系数以重新插入控制顶点，可以在保存几何细节的基础上使曲面更逼近原曲面，也更光顺。

2 升阶光顺法

升阶[11]是 B样条方法配套技术中一项重要技术，通过增加B样条基函数的次数来提高曲面的光顺性，使曲线、曲面更为光顺。B样条曲线升阶的主要方法有：Prautzsch的升阶方法、Cohen等的升阶方法、Piegl等的升阶方法、秦开怀的升阶方法[12]等。采用升阶的方法，即是将B样条函数的次数升高，特别是对于数据点个数变化较大的部分，得到的拟合曲线也更光顺[13]，但加大了数据量。

3 保特征光顺方法

为满足产品的设计意图，要求所设计曲面的光顺性不仅仅要美观，同时也要满足功能上的需求，这就需要在光顺过程中，对曲面特征进行保留，即采用保特征光顺方法。但目前对这类NURBS曲面的保特征光顺问题研究还很少。

另一种对曲面进行光顺的方式是将其转化为网格线的光顺性问题来进行处理。网格光顺的目的是要从原始网格模型中去除噪声，并在局部和整体的体积变形最小化的基础上保持模型的几何形状特征。近年来，一些学者致力于这方面的研究，提出了不少好的保特征的网格光顺算法。Klaus Hildebrandt等[14]融合平均曲率流与各向异性方法定义了各向异性平均曲率向量，并提出了去除噪声保特征的光顺算法。该算法能够保留并加强曲面上的非线性几何特征，如曲面上的弯曲部分、特征线等。Xu Guoliang[15]通过用有限元离散化的方法求解偏微分方程——曲面热流方程(Heat equation），提出的保特征光顺算法能解决曲面光顺不够或过于光顺而丢失细节的问题。目前，这些保特征光顺方法主要集中于基于主曲率、平均曲率等几何流的各向异性融合方法。这些方法虽然能够增强曲面尖锐度，但是对多尺度形状特征并存的曲面光顺还需进一步探讨。

4 基于各向同性小波的曲面光顺算法

近年来，小波分析这种新的时频分析数学方法在NURBS曲线曲面光顺中得到广泛的运用。利用小波的分解与重构算法，可以使B样条曲线曲面具有很好的多分辨特性。因此，可用于B样条曲线曲面的几何造型、光顺处理以及数据压缩等。采用不同的基函数对曲线曲面进行多分辨率分析也会得到不同的结果。Finkelstein[16]提出了在闭区间上基于半正交 B样条小波构造的多分辨率曲线编辑系统。孙延奎、朱心雄等[17]给出了准均匀双二次 B样条曲面小波分解与重构的基本概念，描述了曲面小波分解与重构的快速算法并论述了准均匀 B样条曲线曲面的多分辨分析理论。赵罡等[18]基于多分辨率技术，对曲线、曲面的光顺和编辑进行了研究，实现了在误差控制下准均匀B样条曲线的光顺。

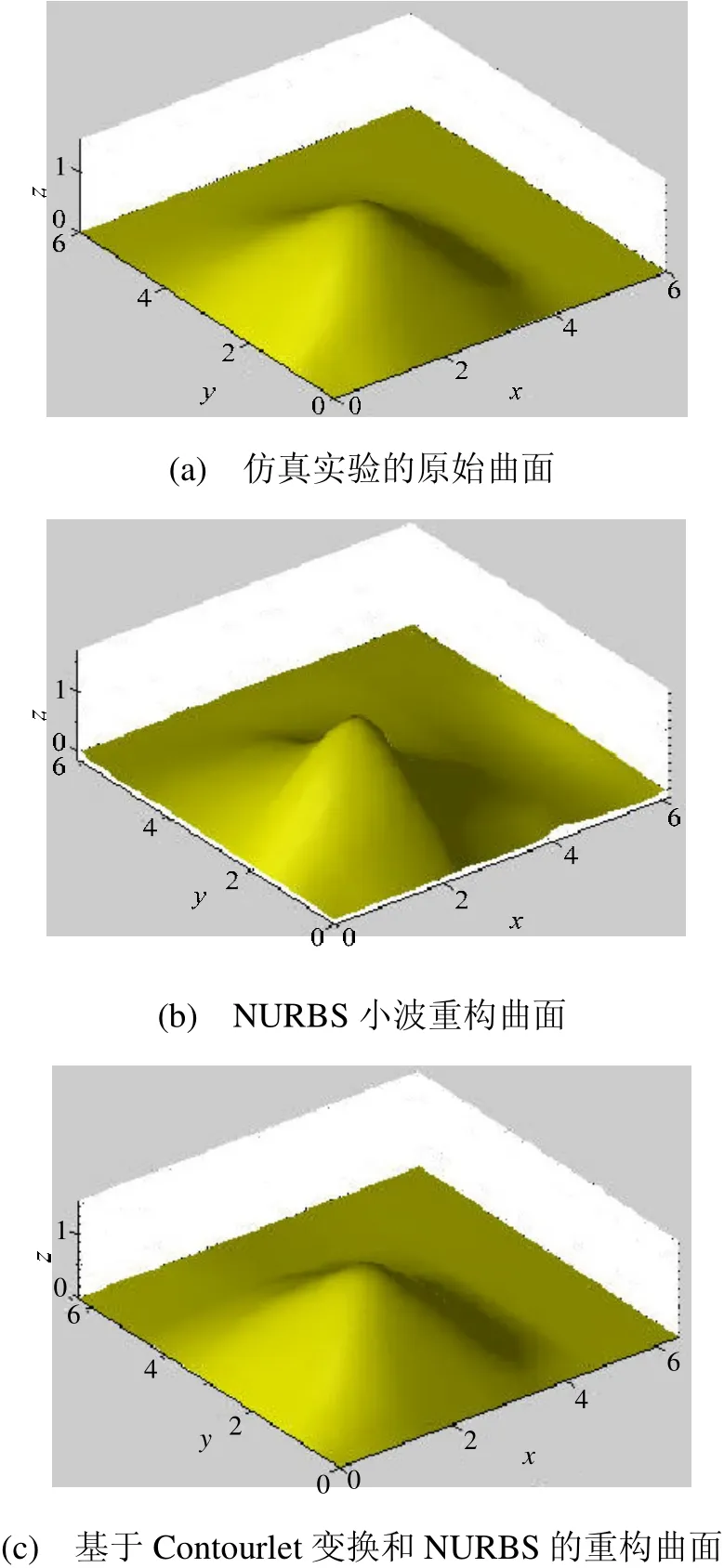
但是准均匀小波光顺算法不能处理边界约束的问题，不适合进行曲线曲面局部光顺。对此，吴维勇[19]提出将能量法与小波光顺法结合，构造分层能量算法，以达到灵活高效地进行曲线局部光顺。然而此算法无法直接应用于任意B样条曲线，需要先对原始曲线进行准均匀B样条曲线逼近，这增加了计算量和计算误差。此外，由于准均匀小波光顺算法要求被光顺 B样条曲线的控制顶点数必须为2j+k（ j为整数，k为B样条曲线的次数）。对此，可以直接插入节点来满足小波光顺对控制点个数的要求[20]。但是这个方法并没有从本质上做出改变。纪小刚等[21]根据多分辨分析的思想，将 m个控制点的曲线用 n(n

由于准均匀 B样条曲线曲面的边界处采用了重节点技术，与定义域内部的小波表达形式不一致，导致在小波重构时计算量较大。对此，赵罡等[22]从几何概念出发论述了基于小波的均匀三次 B样条曲线曲面多分辨表示的原理及其实现。与准均匀B样条曲线曲面采用的半正交小波不同的是，均匀B样条曲线曲面采用的是双正交小波，这使其计算速度更快。但是其小波分解后的边界控制和误差控制还有待于进一步研究。

为了进一步减少小波方法的运算量，出现了基于离散范数l2的双正交非均匀B样条小波基等的分解和重构算法。这种双正交小波只需要尺度函数和小波线性独立，且重构矩阵满足=0，因此小波分解和重构不需要积分运算，计算较简便。根据这一特点，吴福鸣等[23]提出利用双正交非均匀 B样条小波对非均匀 B样条曲面进行光顺的方法。但是这种光顺方法未考虑曲面边界的约束误差精度的控制，较适用于对误差精度要求不高的情况。

为了用小波实现对曲线、曲面的某一个局部进行光顺操作，Lyche[24]给出了非均匀小波的构造。李奇敏等[25]将非均匀 B样条小波分解用于NURBS曲面光顺，通过整体光顺度量确定B样条曲面的光顺方向，实现曲面的整体光顺。同时根据曲面在节点处的光顺性选出曲面上的坏点，通过局部小波分解实现曲面的局部光顺，并通过添加边界约束的方式实现了曲线的保边界光顺。但对于曲面其算法只能保证单参数方向分解时边界不发生变化，因此不具有真正的保边界性。如图1(a)所示为原始曲面，图1(b)所示为经过非均匀小波方法光顺后所得到的曲面，图1(c)所示是经过升阶光顺后的曲面，可以看出光顺的效果要差些。

图1 不同方法对曲面进行光顺

此外，利用细分和提升模式构造的第2代小波也具有计算简单，运算速度快等特点。Martin[26]构造了双正交提升B样条小波用于科学可视化。吴维勇在基于二元提升 B样条小波给出了复杂拓扑曲面小波光顺算法，突破了能量法只能对四边域参数曲面进行光顺的限制，并指出适当修改提升小波规则，可以保留尖角棱边等不连续的特征[27]。

上述这些小波的光顺算法主要适用于具有各向同性奇异性(Isotropic Singularities)的对象，而对于具有各向异性奇异性特征(Anisotropic Singularities)的曲面，上述小波光顺算法均不是很好的工具。因为各向同性小波是可分离的和各向同性的，难以有效地表达图像、图形中带有关键信息的边缘、曲线等更高维的特征，也增加了图像、图形表达的冗余度和处理时间。如图2(a)所示为依次带有s形、矩形、三角形类特征的不光顺曲面，图2(b)所示为经过小波光顺后的曲面，其中黑色部分为光顺中的改变，可以看出为各特征已经没有了原有的形状。

图2 带特征曲面的光顺

5 基于各向异性小波的 NURBS曲面光顺

5.1 各向异性小波

各向异性小波理论是近几年出现的一种新的数学分析方法，它为图像提供了新的稀疏表示方法，能够有效地捕捉信号中的高维奇异特征，从而保留几何结构等重要信息。各向异性小波包括 Ridgelet、Curvelet、Contourlet等。

1998至1999年，D.L Donoho和E.J.Candes提出了脊波变换(Ridgelet Transform)[28]。其本质上是通过对小波基函数添加一个表征方向的参数得到的，因此具有很强的方向选择和辨识的能力，可以非常有效地表示信号中具有方向性的奇异特征，如图像的线性轮廓等。为处理以奇异边界为曲线的对象，Candes在脊波理论的基础上，利用剖分的方法构造了单尺度脊波（Monoscale Ridgelet）。但是，其获得好的逼近性能也是以计算复杂度增加为代价的。

接着，Candes和Donoho在1999年提出第1代曲波变换[29]（Curvelet transform），可以在所有可能的尺度S≥0上进行分解。但是，第1代曲波的数字实现比较复杂，需要子带分解、平滑分块、正规化和脊波分析等一系列步骤，其金字塔的分解也带来了巨大的数据冗余量。因此Candes等人又提出了实现更简单、更便于理解的快速曲波变换算法，即第2代曲波。

在继承了Curvelet变换的各向异性尺度关系的基础上，Donoho和Vetterli于 2002年提出了Contourlet变换[30]，也称为金字塔方向滤波器组(Pyramid Direction Filter Bank, PDFB)。Contourlet变换的优点在于能够在使用少量系数的基础上有效地表示平滑轮廓，而平滑轮廓正是自然图像中的重要特征。目前，Contourlet变换已经在图像重建、压缩、融合等领域有了初步的应用。

图3 基于Contourlet变换和NURBS的重构曲面

参考Contourlet在图像处理中的应用，可以把Contourlet用于曲面处理中。我们把准均匀B样条曲面控制顶点坐标做为变换对象，对其进行Contourlet变换。图3(a)是所用原始曲面，图3(b)是对控制顶点坐标利用小波变换后重构得到的曲面，后者边缘和隆起部分的误差都较明显。可以看出，对于这种特征比较突出的曲面，小波重构方法存在不足。图3(c)是基于Contourlet变换的NURBS重构曲面。与图3(b)对比，前者误差为 0.0046，后者为 0.0034。实验结果表明，Contourlet变换的拟合精度要优于小波变换，具有较高的实际应用价值。

综上所述，这些各向异性小波的出现，为提高曲面多分辨率表达的效率，减少表达的冗余，加快曲面显示、处理的速度等提供了新的思路和方法。

5.2 基于各向异性小波的NURBS曲面光顺

在复杂产品设计中，多尺度特征并存是常见的现象。多尺度特征并存曲面的保特征光顺是多尺度特征并存曲面建模中的关键。而其目的就是要得到满足设计要求的曲面模型，这就需要解决尺度分析、微分几何属性分布规律提取、特征提取、连续性、约束优化等问题。其中微分几何属性分布规律的数学描述、全局约束优化方程的建立及优化算法是实现曲面保特征光顺的难点。目前关于多尺度特征并存曲面的主要处理方法是把基曲面和各个局部特征曲面之间通过剪裁、过渡和搭接等方法实现曲面从整体到局部的造型，这样的造型过程对设计者要求非常高，而且在很多情况下得不到满意的结果。

随着多分辨率分析方法在图形学中的广泛应用，基于小波的多分辨率表达已经被应用到参数曲线，并被推广到张量基曲面、任意拓扑类型曲面、球面及体数据。但是已有的多分辨率曲面表达方法对多尺度特征并存曲面及其上有曲线类特征的曲面表达能力也不足，相应的会带来曲面显示、压缩及传输方面的数据冗余。

基于这种小波多分辨率分析方法，李奇敏提出了平面曲线多尺度分析方法，定义了曲线的局部形状尺度因子，结合去除细节小波重建方法，分析了曲线上各个尺度特征的曲率主要分布规律，实现了大尺度特征在较低分辨率下分析，小尺度特征在较高分辨率下分析，并利用分析结果指导曲线的光顺和特征提取[31]。但是曲面的情况要比平面曲线复杂得多，在分析时既要考虑特征的大小还要考虑特征的方向问题。而基于各向同性小波的多分辨率分析技术对特征方向的表达能力有限，为了提取多尺度特征并存曲面各尺度特征微分几何属性分布规律，有必要把基于各向异性小波的多分辨率分析方法和多尺度分析方法结合起来，对曲面各局部特征主要微分几何信息分布规律进行分析。

如上所述，要实现多尺度特征并存曲面保特征光顺，首先需要建立基于各向异性小波的曲面多分辨率表达和分析框架，用各向异性小波基代替各向同性小波基，把分析相关的Fourier变换、Radon变换等运算推广到张量积曲面和离散曲面，实现曲面的各项异性小波多分辨率分析。

其次，在曲面光顺之前对曲面形状即设计意图进行分析，提取各局部特征尺度，然后基于各向异性小波的多分辨率分析方法对曲面进行多尺度分析，确定各局部特征存在的尺度及其微分几何属性分布规律，然后用数学的语言对该分布规律进行描述，在所得微分几何属性分析基础上提取特征区域的边界、曲线类特征的脊线等特征曲线，并分析各特征间其连续性，以所提取特征曲线和微分几何属性分布规律为约束，利用带约束的全局优化算法实现曲面保形光顺。

6 结束语

本文在总结分析了NURBS曲线曲面各种光顺算法的基础上，详细介绍了小波方法并与其他光顺方法进行了对比。我们指出了小波光顺算法在多尺度特征并存曲面保特征光顺上的不足，提出了将各向异性小波融入曲面的多分辨率分析中的思想和实现这种方法的思路。我们将继续对该问题进行更详细的研究。

[1]马利庄, 石教英. 曲线曲面的几何光顺算法[J]. 计算机学报, 1996, 19: 210-216.

[2]朱心雄. 自由曲线曲面造型技术[M]. 北京:科学出版社, 2000: 358-360.

[3]蒋大为, 李安平. B样条曲线的最小二乘保形光顺逼近[J]. 工程数学学报, 2000, 17(1): 125-128.

[4]Lott N J, Pullin D I. Method for fairing B-spline surfaces [J]. Computer-Aided Design, 1988, 20(10):597- 604.

[5]Moreton H P, Sequin C H. Functional optimization for fair surfaces design [J]. Computer Graphics, 1992,26(2): 167-175.

[6]穆国旺, 朱心雄, 涂侯杰, 等. 曲面光顺的分片能量法[J]. 工程图学学报, 1999, (1): 29-34.

[7]Zhang Caiming, Zhang Pifu, Cheng Fuhua. Fairing spline curves and surfaces by minimizing energy [J].Computer-Aided Design, 2001, 33(13): 913-923.

[8]王莹莹, 刘德平, 陈建军, 等. 基于曲率均化的B样条曲线能量光顺方法[J]. 机床与液压, 2010, 38(3):94- 96.

[9]胡海艳, 吴振远. 基于广义逆矩阵的 8样条曲线的节点消去与光顺[J]. 工程地球物理学报, 2010, 7(2):106- 110.

[10]Bertram M. Single-knot wavelets for non-uniform B-splines [J]. Computer Aided Geometric Design,2005, 22(9): 849-864.

[11]施法中. 计算机辅助几何设计与非均匀有理 B样条[M]. 北京: 高等教育出版社, 2001: 285-293.

[12]秦开怀. 非均匀B样条曲线升阶的新算法[J]. 计算机学报, 1996, 19(7): 537-542.

[13]曹利新, 游 洪. 基于升阶的 B 样条曲面光顺拟合[J]. 机械制造, 2003, 41(7): 23-25.

[14]Hildebrandt K, Polthier K. Anisotropic filtering of non-linear surface features [C]//Eurographics 2004 Comput Graph Forum, 2004: 391-400.

[15]Xu Guoliang. Surface fairing and featuring by mean curvature motions [J]. Journal of Computational and Applied Mathematics, 2004, 163(1): 295-309.

[16]Finkelstein D H, Salesin. Multiresolution curves [C]//Proceedings of SIGGRAPH. ACM, 1994: 261-268.

[17]孙延奎, 朱心雄, 唐 龙, 等. 准均匀 B 样条曲面小波分解的快速算法[J]. 清华大学学报(自然科学版), 2001(z1): 209-213.

[18]赵 罡, 穆国旺, 朱心雄. 基于小波的准均匀 B样条曲线曲面变分造型[J]. 计算机辅助设计与图形学学报, 2002, (1): 61-65.

[19]吴维勇, 王小椿. 自由曲线局部光顺的分层能量算法[J]. 计算机辅助设计与图形学学报, 2002, 14(10):959-966.

[20]潘洋宇, 姜福祥. 任意控制点曲线小波光顺方法研究[J]. 机械设计, 2009, 26(11): 12-13.

[21]纪小刚, 龚光容. 准均匀三次B样条曲线的任意分辨率光顺[J]. 机械科学与技术, 2009, 28(11): 1477-1481.

[22]赵 罡, 穆国旺, 闫光荣, 等. 均匀 B 样条曲线曲面的小波表示[J]. 工程图学学报, 2001, (1): 80-87.

[23]吴福鸣, 潘日晶. 基于双正交非均匀B样条小波的曲面光顺[J]. 福建师范大学学报(自然科学版),2010, (1): 33-37.

[24]Lyche T, Mrken K. Spline-wavelets of minimal support [J]. Numerical Methods of Approximation Theory, 1992, (9): 177-194.

[25]李奇敏, 柯映林, 何玉林. 基于非均匀B样条小波的NURBS曲面光顺[J]. 中国机械工程, 2007, 18(5):577-582.

[26]Bertram M, Mark A D, Hamann B, el at. Bicubic subdivision-surface wavelets for large-scale isosurface representa-tionand visualization [C]//Proceedings of IEEE Visualization, 2000:389-396&579.

[27]吴维勇. 自由曲线曲面多分辨率造型技术研究与应用[D]. 西安: 西安交通大学, 2003.

[28]Emmanuel J, Candès, David L, et al. Ridgelets:a key to higher-dimensional intermittency [C]//Phil. Trans.R. Soc. Lond. A. 1999: 2495-2509.

[29]焦李成, 谭 山, 刘 芳. 脊波理论: 从脊波变换到 Curvelet变换[J]. 工程数学学报, 2005, 22(5):761-773.

[30]Lounsbery M, De R T, Warren J. Multiresolution analysis for surfaces of arbitrary topological type [J].ACM Transaction on Graphics, 1997, 16(1): 34-73.

[31]李奇敏. 小波在反求工程中的若干应用[D]. 杭州:浙江大学, 2006.