预应力混凝土简支箱梁足尺模型试验及非线性全过程分析
方 志,唐盛华,何 鑫
(湖南大学土木工程学院,长沙 410082)
1 前言
结构破坏性试验可以真实地记录全桥位移、应变、裂缝等随荷载的发展及结构的破坏形式。混凝土作为一种复杂的复合工程材料,其力学行为和破坏规律尚需进一步探索。足尺模型试验与缩尺模型试验相比,不存在相似比、材料和结构的尺寸效应等的影响,试验结果直观可靠,但由于足尺模型试验难度大、成本高等原因,目前进行的桥梁足尺模型试验研究还很少。迄今国内外研究者结合一些桥梁的改建对几座拟拆除桥梁进行了破坏性的试验[1~3],但鲜见对独立的预应力混凝土简支箱梁进行足尺试验的文献报道[4]。
混凝土结构受力变形存在较为明显的非线性现象,目前,混凝土结构的非线性分析主要有以下几种方法。
1)通过现有大型通用有限元软件实现[5~7],例如ANSYS、ADINA等。由于这类通用软件目前的非线性计算能力还很有限,因而在实际使用时,需要反复调整参数,以使计算收敛。
2)基于新单元的有限单元法。例如,采用三维实体退化虚拟层合单元的分析方法[8],能反映预应力钢筋与混凝土间相对滑移和相互作用的单元模型[9]。此类方法较第一种有一定的改进,但仍难以计算荷载-位移下降段曲线。
3)专业的程序进行计算。使用TEXSLAB对两跨连续后张法预应力板桥模型进行分析[10],使用NONBAN对两根预应力组合梁及实桥进行计算[11],但均未提及荷载-位移曲线的下降段。
4)基于平截面假定的有限条带法[12]。该方法基于截面的弯矩-曲率关系曲线计算结构的荷载-位移曲线,因而可以直接对截面的承载力进行验算,此外,还可以较好地实现荷载-位移曲线下降段的计算。
对一片30 m跨的预应力混凝土小箱梁和一片20 m跨的预应力混凝土空心板进行了破坏性实验,完整记录了试验过程中位移、应变等随荷载的变化情况。基于平截面假定,采用有限条带法编制了非线性计算程序,可对包括卸载过程在内的全过程受力性能进行分析。
2 试验介绍
2.1 基本情况
试验以荆岳长江公路大桥北岸引桥一片30 m跨的预应力混凝土小箱梁和一片20 m跨的预应力混凝土空心板为测试对象。荆岳长江公路大桥北岸引桥为先简支后连续的装配式预应力混凝土箱梁桥,小箱梁和空心板的半立面分别如图1和图2所示。小箱梁跨中截面尺寸及配筋如图3所示,试验梁计算跨径为29.0 m,梁中心处高1.8 m,混凝土设计强度等级为C50,普通钢筋除图3中①号钢筋为φ16 HRB335钢筋外,其他均为 φ10 R235钢筋,预应力筋采用公称直径为15.24 mm的高强、低松弛钢绞线,其标准抗拉强度fpk=1 860 MPa,张拉控制应力为1 395 MPa,松弛率≤2.5%。箱梁共配8束,每束4根预应力筋。空心板跨中截面尺寸及配筋如图4所示,试验梁计算跨径为19.0 m,梁高0.9 m,混凝土设计强度等级为C40,普通钢筋均为φ8 R235,预应力筋的材料特性与小箱梁相同,共配4束,每束7根预应力筋。
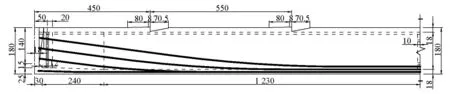
图1 小箱梁半立面布置(单位:cm)Fig.1 Semi-elevation layout of box girder(unit:cm)

图2 空心板半立面布置(单位:cm)Fig.2 Semi-elevation layout of hollow slab(unit:cm)
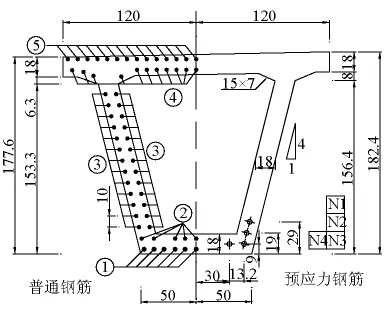
图3 1-1截面(单位:cm)Fig.3 1 -1 section(unit:cm)
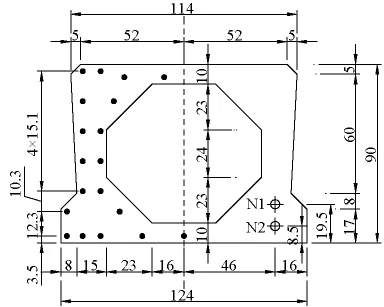
图4 2-2截面(单位:cm)Fig.4 2 -2 section(unit:cm)
2.2 材料特性
混凝土的材料特性见表1,预应力钢筋和普通钢筋的材料特性见表2,其中预应力筋的屈服抗拉强度采用名义屈服强度σ0.2。

表1 混凝土材料特性Table 1 Material properties of concrete

表2 钢筋材料特性Table 2 Material properties of reinforcement
2.3 加载装置和测试方案
试验采用跨中反力架单点重复加载,在分配梁底部布置一对压力传感器以控制荷载大小。小箱梁试验加载装置如图5所示。试验主要测定箱梁的荷载-位移(P-Δ)曲线、截面应变状态以及裂缝特征等。空心板的加载装置和测试方案同小箱梁。

图5 试验加载装置Fig.5 Test loading device
3 试验结果分析
3.1 荷载-位移曲线
小箱梁和空心板跨中截面的荷载-位移曲线分别如图6、图7所示。由图6可以看出,小箱梁跨中截面的荷载-位移曲线包络线近似呈四折线,其折点分别是混凝土开裂(A点)、普通钢筋屈服(B点)及预应力钢筋屈服(C点)。空心板跨中截面的荷载-位移曲线包络线近似呈三折线,其折点分别是混凝土开裂(G点)和普通钢筋屈服(H点)。小箱梁和空心板均具有良好的变形能力,其跨中最大挠度分别达到了跨径的1/99和1/104。
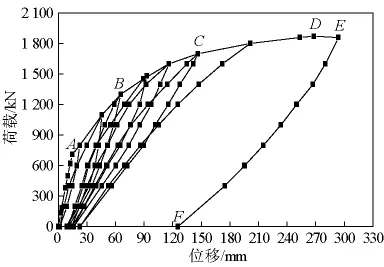
图6 小箱梁跨中荷载-位移曲线Fig.6 Mid-span load -displacement curves of box girder
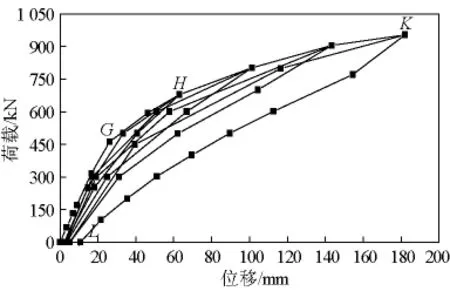
图7 空心板跨中荷载-位移曲线Fig.7 Mid-span load -displacement curves of hollow slab
3.2 应变分析
小箱梁和空心板跨中截面顶板混凝土荷载-应变曲线分别如图8、图9所示。由图8可知,小箱梁当荷载达到1 872 kN时,跨中截面顶板混凝土压应变为1 520 με(με 为微应变,即 10-6个应变,无量纲),与混凝土的极限压应变相差较远。由于荷载-位移曲线在加载过程中出现荷载下降现象,可以推断如果继续加载,结构破坏将由预应力钢筋的拉断引起,基于安全因素考虑,当加载过程中出现荷载下降现象时应终止试验。由图9可知,空心板临近破坏时,顶板混凝土的应变增加很快,荷载为900 kN和920 kN时对应的应变分别为1 822 με和2 370 με,试验梁破坏荷载为954 kN,结构的破坏由顶板混凝土压碎引起。
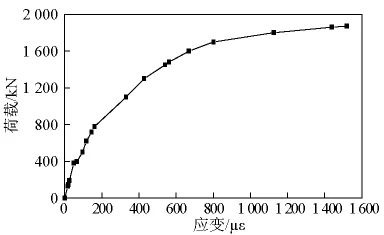
图8 小箱梁顶板混凝土荷载-应变曲线Fig.8 Roof concrete load - strain curves of box girder
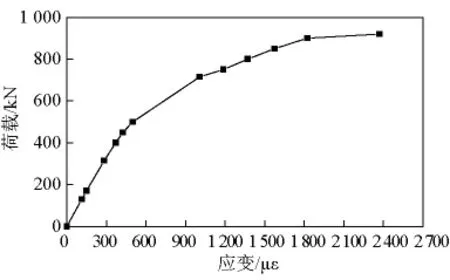
图9 空心板顶板混凝土荷载-应变曲线Fig.9 Roof concrete load - strain curves of hollow slab
3.3 延性分析
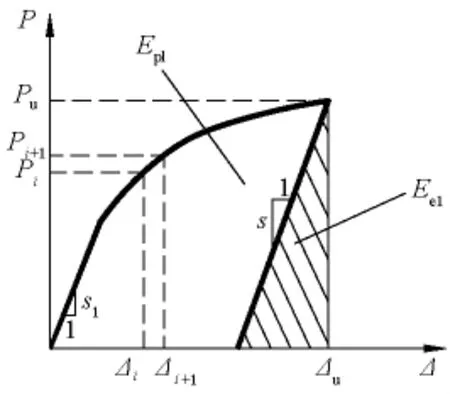
结构破坏前所产生的大变形并不意味着结构一定具有好的延性,或许仅有好的变形能力。结构的延性仅取决于结构的非弹性变形或耗能能力。基于Naaman和Jeong采用能量的观点来定义延性指标[13]
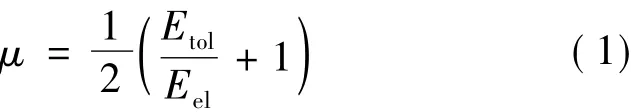
式(1)中,Etol为总能量,Etol=Eel+Epl;Eel为弹性能量;Epl为塑性能量,其值可借助图10所示结构的荷载-位移(P-Δ)曲线所包围的相应部分的面积确定,位移初始位置取试验加载前的位置。由式(1)及小箱梁和空心板跨中荷载-位移曲线可得其延性指标分别为1.99和1.23。
4 数值分析
基于平截面假定,采用有限条带法编制了预应力混凝土简支梁非线性分析程序[14]。
4.1 基本假定
1)梁正截面变形后仍保持为平面,截面应变为直线分布;
2)钢筋与混凝土黏结良好,不发生相对滑移;3)不考虑剪切变形的影响;
4)结构的破坏指梁发生弯曲破坏,即梁顶缘混凝土压碎或者预应力钢筋拉断。
4.2 材料本构关系
4.2.1 混凝土本构关系
选用单轴作用下的受压受拉本构方程[15]
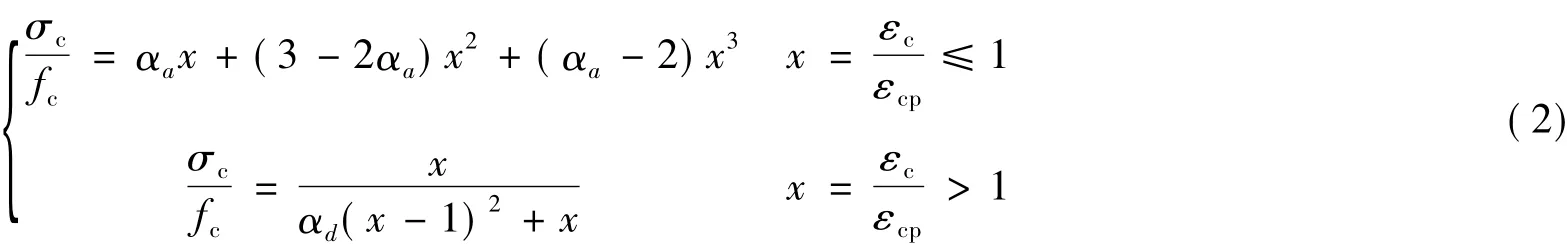
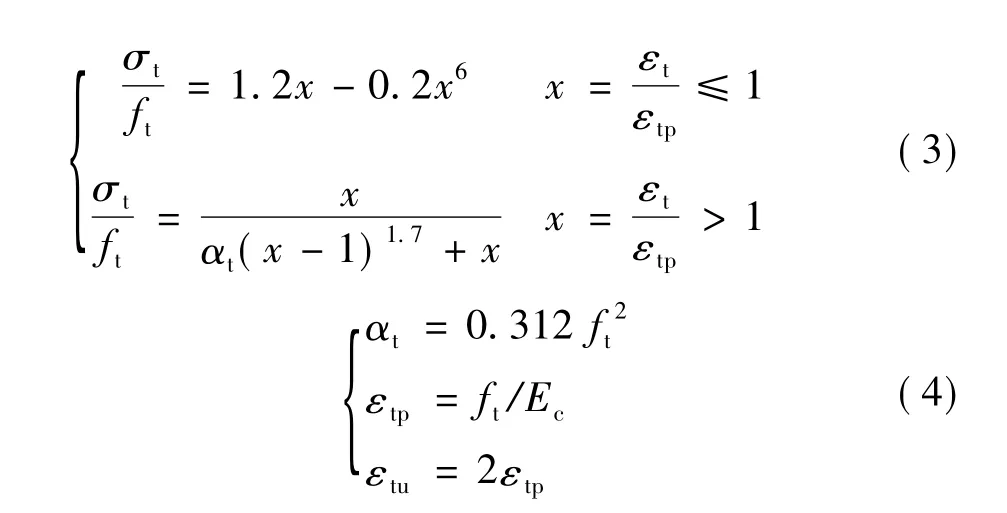
式(2)~(4)中,σc和εc分别为混凝土的压应力和压应变;fc和εcp分别为混凝土的棱柱体抗压强度和刚好达到fc时对应的应变,取εcp=2 000 με,混凝土的极限压应变εcu=3 300 με;αa和αd为参数,当 αa=2.0,αd=0 时,方程变为 Rusch建议的公式;Ec为混凝土的弹性模量;下标t表示受拉,其参数含义同受压参数,程序中混凝土抗拉强度采用标准值。
4.2.2 普通钢筋本构关系
普通钢筋受拉受压采用相同的本构关系曲线,为弹性-强化模型[15]
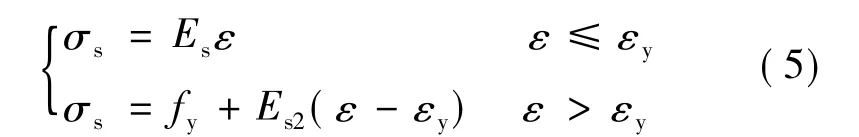
式(5)中,σs和ε分别为钢筋的应力和应变;fy和εy分别为钢筋的屈服应力和应变;Es和Es2分别为钢筋屈服前后的弹性模量。
4.2.3 预应力钢筋的本构关系
预应力钢筋的受拉本构方程如下[15]:
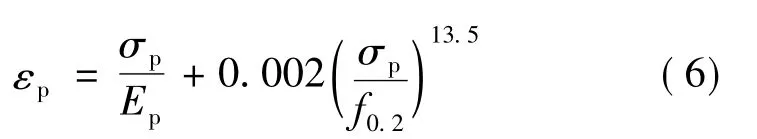
式(6)中,σp和εp分别为预应力钢筋的应力和应变;Ep为预应力钢筋的弹性模量;f0.2为预应力钢筋的名义屈服应力。实测小箱梁和空心板的预应力钢筋延伸率分别为3.1%和3.5%,有效预应力均约为1 138 MPa。
4.2.4 卸载本构曲线
卸载时,材料的应力-应变按线性关系处理,极限应变时卸载弹性模量取E1,0~εu按线性插值进行计算,如图11所示,图中E0为初始弹性模量,
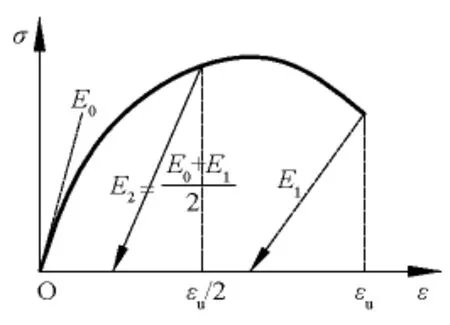
图11 应力-应变曲线Fig.11 Stress-strain curve
4.3 弯矩-曲率(M-φ)关系
构件卸载时,各梁段的弯矩不同,因而截面的应变分布也不同,小箱梁跨中截面加载至顶板应变为εtop后进行卸载,其弯矩-曲率关系如图12所示。观察发现其不同应变卸载曲线基本平行,因而,程序计算时,只计算εtop=εu时的卸载曲线,然后将其平移,得到加载至任意应变卸载的卸载曲线,如图13所示,当卸载曲率与加载曲线相交时,如图中A点,卸载曲线取加载曲线的AO段。
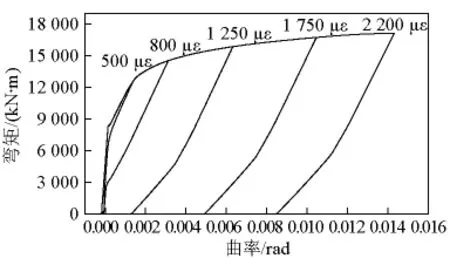
图12 小箱梁弯矩-曲率曲线Fig.12 Moment-curvature curves of box girder
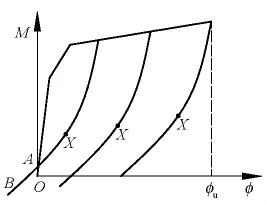
图13 弯矩-曲率曲线Fig.13 Moment-curvature curves
4.4 荷载-位移曲线计算
荷载-位移曲线采用共轭梁法进行计算,小箱梁和空心板的分段数目分别为151和101,此时,梁段长度约为0.2 m。材料本构参数取值见表3。荷载-位移曲线数值计算结果与实测值的比较如图14、图15所示,其中卸载曲线采用σ-ε、M-φ及P-Δ这3个层面进行了计算。σ-ε层面卸载时,如4.3节所述。由图14、图15可以看出,程序计算的荷载-位移曲线的上升段与实测数据很接近,3种层面计算的卸载曲线也比较接近,与实测数据吻合较好,其中P-Δ层面计算的卸载曲线为直线。程序计算的小箱梁和空心板的延性指标分别为1.73 和 1.23。

表3 本构参数取值Table 3 Stress-strain parameters value
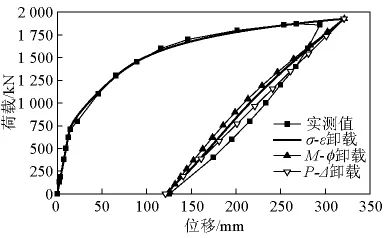
图14 小箱梁荷载-位移曲线Fig.14 Load -displacement curves of box girder
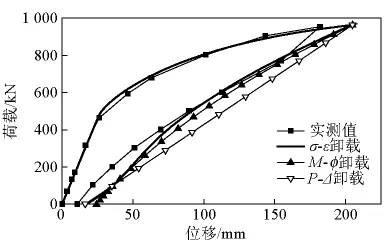
图15 空心板荷载-位移曲线Fig.15 Load - displacement curves of hollow slab
参考图10,荷载-位移曲线的加权刚度定义如式(7)所示,式中上标P表示P-Δ曲线的加权刚度,M表示M-φ曲线的加权刚度。
二是抓好研究选题。重点围绕保障水安全、水利现代化、水生态文明建设等战略问题,水资源管理、水利工程建设和管理、水利投入、水权水价水市场等体制机制问题,水利法制建设、水行政管理改革、水利行业能力建设、基层水利发展等管理问题,摸清情况,理出思路,寻找对策,提出方案。
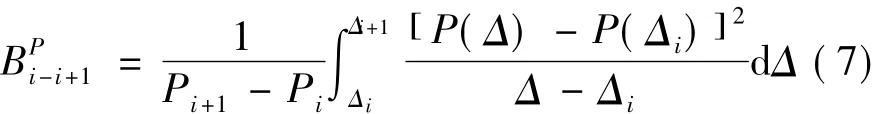
弯矩-曲率曲线的加权刚度计算只需将式中的荷载和位移替换成弯矩和曲率即可。由截面弯矩-曲率关系曲线及荷载-位移曲线的上升段可以计算各段曲线的刚度如表4所示,表中“屈服”表示受拉区面积最大的一层普通钢筋屈服。
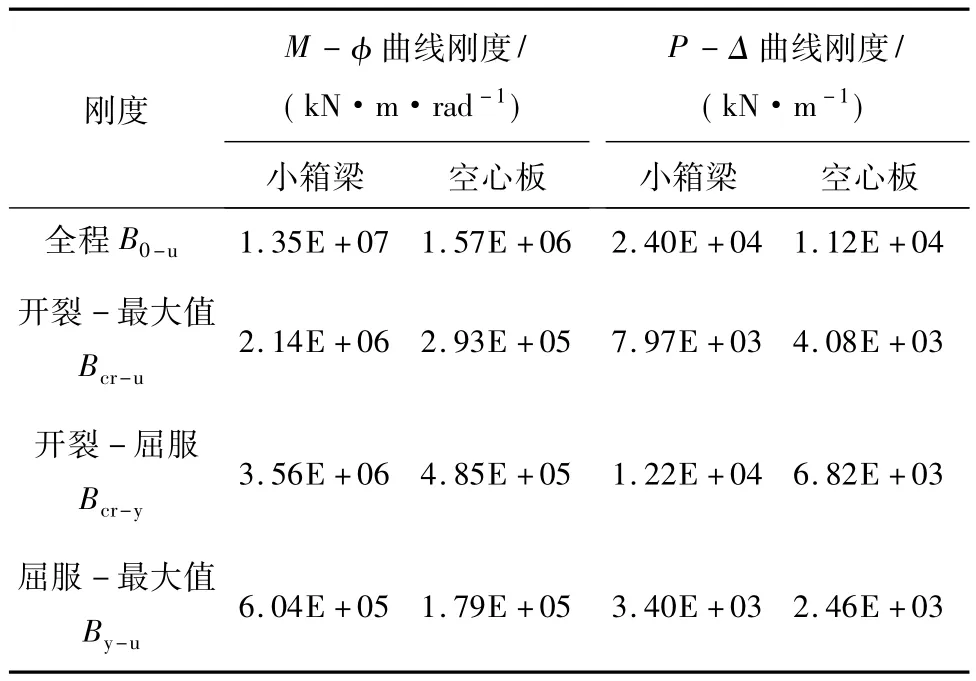
表4 弯矩-曲率和荷载-位移曲线刚度Table 4 Stiffness of moment-curvature andload-displacement curves
观察图12可以看出,σ-ε层面计算的卸载曲线的第一段与开裂后至普通钢筋屈服前的曲线基本平行,因而M-φ层面卸载时,使用弯矩-曲率关系曲线开裂至普通钢筋屈服段的刚度BMcr-y作为卸载曲线的刚度。P-Δ层面卸载时,卸载曲线的刚度取的调和平均数,见式(8)。
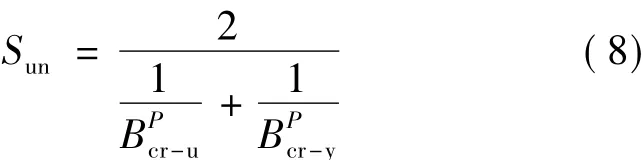
实测P-Δ曲线数据点数相对较少,采用式(8)计算的卸载刚度偏小,文献[16]采用P-Δ曲线从加载至极限荷载的全程加权刚度进行计算,见式(9)。

式中,γ为加载方式影响因子,对于跨中单点加载,当取γ=0.5时,小箱梁和空心板的计算结果与实测值都比较接近,如图16、图17所示,说明γ取值合理。
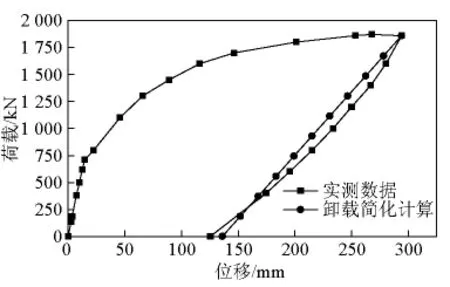
图16 小箱梁卸载简化计算Fig.16 Simplified unloading curve of box girder
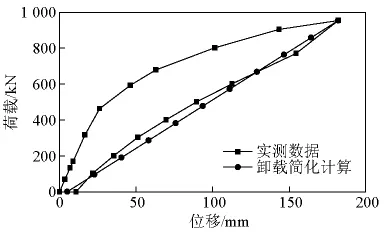
图17 空心板简化计算卸载Fig.17 Simplified unloading curve of hollow slab
5 参数分析
基于非线性程序,对部分参数进行了分析,卸载曲线均使用σ-ε层面卸载曲线进行计算。
5.1 预应力筋配筋量的影响
平衡配筋量是指预应力筋断裂的同时混凝土压碎破坏所对应的预应力筋量,配筋率按 ρp=Ap/bwh0计算,通过改变每束预应力筋中钢铰线的根数,由程序试算得到小箱梁和空心板平衡配筋量对应的每束钢绞线根数n分别为7.7和3.1(配筋率ρ为1.40%和0.67%),实际配筋量为每束4根和7根。小箱梁和空心板不同配筋量下跨中截面的P-Δ曲线如图18、图19所示,延性指标如图20、图21所示。
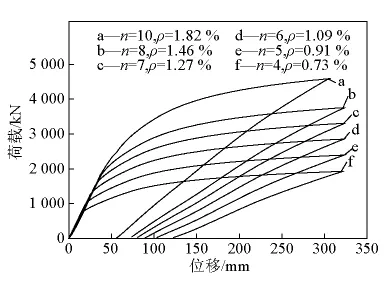
图18 小箱梁预应力筋不同配筋量荷载-位移曲线Fig.18 Load - displacement curves of box girder under different quantities of prestressed reinforcement
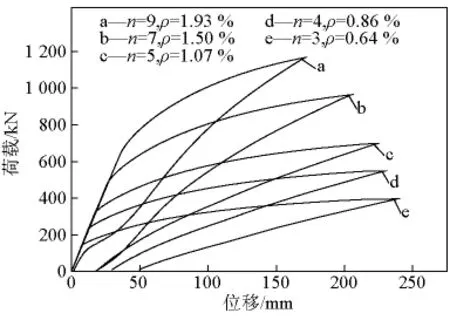
图19 空心板预应力筋不同配筋量荷载-位移曲线Fig.19 Load - displacement curves of hollow slab under different quantities of prestressed reinforcement
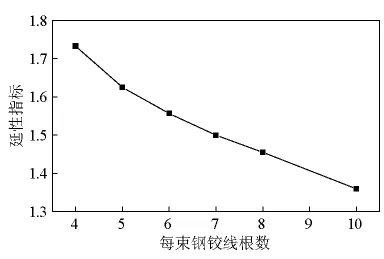
图20 小箱梁延性指标-配筋量曲线Fig.20 Ductility index and quantity of reinforcement curve of box girder
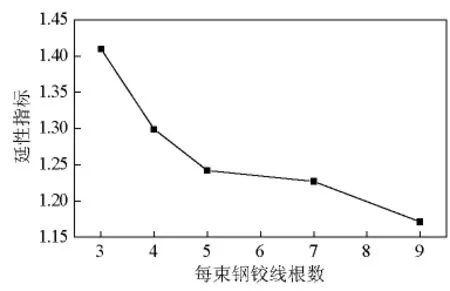
图21 空心板延性指标-配筋量曲线Fig.21 Ductility index and quantity of reinforcement curve of hollow slab
从图18~图21中可以看出如下几点。
1)当截面的配筋量小于平衡配筋量时,结构的破坏由预应力筋拉断造成,此时,增加预应力筋的数量不会对结构的最大变形造成影响,但残余变形会减小。
2)当截面的配筋量大于平衡配筋量时,结构的破坏由混凝土压碎造成,此时,增加预应力筋的数量会使结构的变形性能变差。
3)结构的极限承载能力随着配筋量的增加明显增大,残余变形和延性指标随着配筋量的增加而减小。当配筋量小于平衡配筋量时,结构延性指标随配筋量增加的下降速度较快,当配筋量大于平衡配筋量时,下降速度变慢。
4)小箱梁和空心板配筋量每束分别为8根和3根时计算的延性指标为1.455和1.410,此时的配筋量与平衡配筋量相近,延性指标基本一样,说明预应力筋的配筋量是造成两根试验梁受力性能差异较大的主要原因。
5.2 预应力筋张拉系数的影响
定义预应力筋张拉系数η为

式(10)中,fp和σeff分别为预应力筋标准抗拉强度及其有效预应力。改变预应力筋张拉系数η的大小,计算得到小箱梁和空心板的跨中荷载-位移曲线如图22、图23所示。
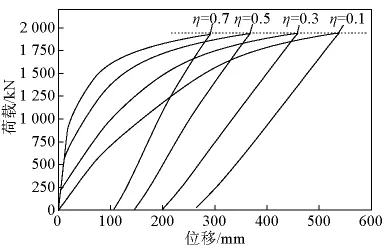
图22 小箱梁不同张拉系数下荷载-位移曲线Fig.22 Load -displacement curves of box girder under different tension coefficients
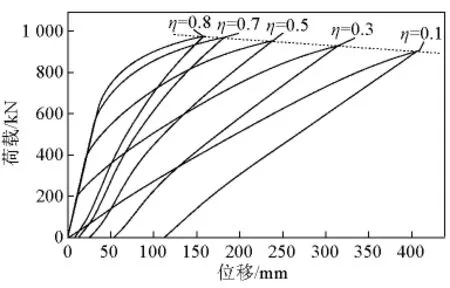
图23 空心板不同张拉系数下荷载-位移曲线Fig.23 Load - displacement curves of hollow slab under different tension coefficients
从图22和图23中可以看出:
1)张拉系数对于小箱梁极限承载力的大小没有影响,而对空心板有一定的影响,张拉系数为0.1和0.8所对应的极限荷载分别为901 kN和973 kN。由此可得出以下结论:对于以预应力筋的拉断造成破坏的构件,张拉系数对承载力没有影响,而对于以顶板混凝土的压碎造成破坏的构件,随着张拉系数的增加,承载力会有所增加。因为预应力筋张拉使截面上缘产生拉应变ε0,构件破坏时截面顶缘应变为 εu,其增量为 εu-0= εu- ε0,当以混凝土压碎造成破坏时,εu-0的值会增加,破坏时截面的受压区高度也会相应地增大,使得承载力增加。
2)随着张拉系数的增加,结构的最大变形和残余变形均显著减小,结合上述的分析结果,设预应力筋有效预应力对应的应变为εeff,结构破坏时预应力筋的应变为 εpu,其应变增量为 εΔp= εeff- εpu,即当εΔp增加时,结构的变形能力增加。当预应力筋张拉系数一定时,若构件以预应力筋拉断造成破坏,由于此时εΔp均相同,因而尽管预应力筋的配筋量不同,构件破坏时的最大变形也相同。若构件以混凝土压碎造成破坏,此时,预应力筋配筋量越大,εpu越小,使得εΔp减小,从而最大变形也变小。由于预应力筋张拉系数直接决定εeff的大小,因而其对构件变形性能的影响比预应力筋配筋量的影响要大。
3)随着张拉系数的增加,截面的轴压比增加,结构的延性指标下降,但变化较小,小箱梁张拉系数从0.1 增加到0.7,延性指标从1.837 下降到1.727;空心板张拉系数从0.1增加到0.8,延性指标从1.231下降到 1.210。
6 结语
1)对一片30 m跨的预应力混凝土小箱梁和一片20 m跨的预应力混凝土空心板进行了足尺模型试验,破坏模式分别为预应力筋拉断和顶板混凝土压碎,按能量的观点计算的延性指标小箱梁和空心板分别为 1.99 和1.23。
2)编制了非线性计算程序,重点介绍了卸载曲线采用σ-ε、M-φ及P-Δ这3个层面是如何进行计算的。3种层面计算的卸载曲线比较接近,与实测数据吻合较好,同时,对于实测的荷载-位移曲线,采用简化方法计算了其卸载曲线,效果良好。
3)承载力:结构的极限承载能力随着配筋量的增加明显增大。对于以预应力筋的拉断造成破坏的构件,预应力筋张拉系数对承载力没有影响,而对于以顶板混凝土的压碎造成破坏的构件,随着张拉系数的增加,承载力会有所增加。
4)变形性能:预应力筋从加载到破坏时的应变增量越大,构件的变形性能越好。预应力筋张拉系数对构件变形性能的影响比预应力筋配筋量要大。
5)延性:延性指标随着预应力筋配筋量的增加而降低,当小箱梁和空心板均为平衡配筋量时,二者的延性指标基本相同。延性指标随着预应力筋张拉系数的增加而降低,其影响较预应力筋配筋量的影响要小。
[1]Miller R A,Aktan A E,Shahrooz B M.Destructive testing of decommissioned concrete slab bridge[J].Journal of Structural Engi-neering,1994,120(7):2176-2198.
[2]谢家全,吴赞平,华 斌,等.沪宁扩建桥梁极限承载能力实桥试验研究[J].现代交通技术,2006(5):77-84.
[3]张 蓓,徐天昭,王复明,等.预应力混凝土空心板梁桥承载能力实桥试验研究[J].公路,2008(6):1-5.
[4]邹毅松,徐向茜.20 m跨径后张预应力混凝土空心板梁变形的试验研究[J].重庆建筑大学学报,1999,21(2):70-73.
[5]Cheng H T,Mohammed B S,Mustapha K N.Experimental and analytical analysis of pretensioned inverted T-beam with circular web openings[J].International Journal Mechanics and Material in Design,2009(5):203-215.
[6]李义强,彭正中,王新敏.基于ANSYS的钢筋混凝土简支梁极限承载力分析[J].石家庄铁道学院学报,2006,19(1):22-26.
[7]张 彬,李治国.基于ADINA的预应力箱梁承载能力非线性有限元分析[J].辽宁工程技术大学学报:自然科学版,2008,27(5增刊):62-64.
[8]吴光宇,汪劲丰,项贻强,等.钢筋混凝土箱形梁极限承载力的计算[J].浙江大学学报:工学版,2007,41(1):161-165.
[9]吴晓涵.预应力混凝土结构非线性有限元分析[J].建筑结构学报,2007,28(4):83 -89.
[10]Paul N Roschke,Kevin R Pruski.Overload and ultimate load behavior of posttensioned slab bridge[J].Journal of Bridge Engineering,2000,5(2):148-155.
[11]Deng Linzhong,Michel Ghosn,Ales Znidaric,et al.Nonlinear flexural behavior of prestressed concrete girder bridges[J].Journal of Bridge Engineering,2001,6(4):276 -284.
[12]薛 刚,郭晓燕.钢筋混凝土梁抗弯刚度非线性全过程分析[J].内蒙古科技大学学报,2007,26(3):250-252.
[13]Naaman A E,Jeong S M.Structural ductility of concrete beams prestressed with FRP tendons[C]//Non-metallic(FRP)Reinforcement for Concrete Structures.Quebec,1995:379 -386.
[14]吕西林.钢筋混凝土结构非线性理论与应用[M].上海:同济大学出版社,1997.
[15]过镇海,时旭东.钢筋混凝土原理和分析[M].北京:清华大学出版社,2003.
[16]Grace N F,Soliman A K,Abdel S G,et al.Behavior and ductility of simple and continuous FRP reinforced beams[J].Journal of Composites for Construction,1998,2(4):186-194.

