基于双参数模型参考自适应的感应电机无速度传感器矢量控制低速性能

尹忠刚 刘 静 钟彦儒 杨立周

（西安理工大学电气工程系 西安 710048）

1 引言

近年来在交流电动机矢量控制系统中，为了克服使用机械传感器带来的高成本、安装维护困难、抗干扰能力下降、可靠性降低等缺陷，通过各种不同的估计方法而得到速度和位置信息的无速度传感器技术，已成为电机控制领域中的研究热点之一。

目前，模型参考自适应（Model Reference Adapt System，MRAS）因其具有算法不太复杂、抗干扰性能好、保证参数估计的渐进收敛性、稳态精度较高等优点而受到人们重视，已经被提出并应用于感应电机无速度传感器矢量控制中[1-11]。

根据参考模型及可调模型的不同选择，有多种MRAS 转速估计方法，其中研究最多的是以电压模型作为参考模型，以含转速信息的电流模型作为可调模型的经典MRAS 转速估计法[1,3,5]，该算法实用性强，但存在积分初值和漂移问题。文献[1,2]采用了基于反电动势的MRAS 转速估算方案，但由于在低速时反电动势很小，且在转速过零时变化缓慢，使得算法对定子电阻的变化较为敏感，导致估计不准确甚至不收敛。为了增加算法的鲁棒性，消除定子电阻等电机参数变化的影响，文献[3,4]提出了利用瞬时无功功率构造 MRAS的参考模型和可调模型，这一方法的参考模型和可调模型中均不含定子电阻，但是以发电模型下的稳定性为代价。文献[5,6]采用V*×I的瞬时值作为参考模型，以磁场定向方式下V*×I的稳态值作为可调模型，可以四象限运行，但是其在可调模型中引入了定子电阻，且算法是以磁场定向和稳态为前提的，因此，不能保证动态过程中磁场定向是否能准确实现。然而，无论何种MRAS 方法，定子电阻压降、积分直流偏置等都是不可忽视的因素，它会导致MRAS 在低速时转子磁链的观测精度不高，从而影响系统在低速时的转速估算精度和带载性能。

本文提出了一种基于双参数MRAS的感应电机无速度传感器矢量控制策略，可以同时进行转速辨识和定子电阻辨识，能够有效削弱低速时定子电阻变化对系统的影响，并且采用惯性环节代替纯积分环节，可以有效地解决积分初值的问题，提高了系统的低速带载性能；推导了转速闭环系统的线性化小信号模型，利用根轨迹法分析了系统的稳定性及PI 参数对系统性能的影响，实验结果验证了算法的有效性。

2 基于MRAS的转速估算原理

MRAS 是一种基于稳定性设计的参数辨识方法，保证了参数辨识的渐进收敛。其主要思想是将不含未知参数的方程作为参考模型，而将含有待辨识参数的方程作为可调模型，利用两个模型具有相同物理意义的输出量的误差构成合适的自适应律来实时调节可调模型待辨识的参数，最终达到控制对象的输出跟踪参考模型的目的。

两相静止坐标上的转子磁链电压模型可以表示为

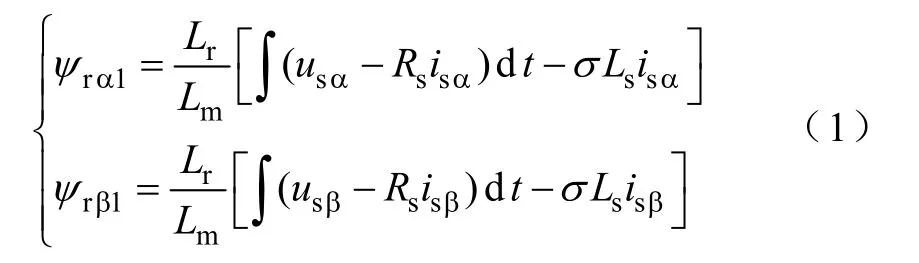
式中ψrα1，ψrβ1——使用电压模型时转子磁链在 αβ 轴的分量；

usα，usβ——定子电压在αβ 轴的分量；

isα，isβ——定子电流在αβ 轴的分量；

Ls，Lr——定、转子电感；

Lm——互感；

Rs——定子电阻；

σ——漏磁系数，且σ=1-(Lm2/LsLr)。

两相静止坐标上的转子磁链电流模型表示为

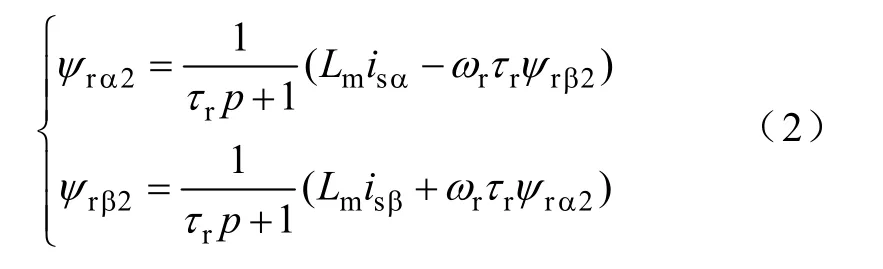
式中ψrα2，ψrβ2——使用电流模型时转子磁链在αβ 轴的分量；

ωr——转子转速；

τr——转子时间常数，且τr=Lr/Rr。

从式（1）、式（2）可以看出，电压模型和电流模型具有相同物理意义的输出量转子磁链，并且电压模型与转速无关，因此将电压模型作为参考模型，将含有电机转速的电流模型作为可调模型，把辨识的转速反馈给电流模型，当两个模型的输出一致时，估算转速趋于实际转速，原理框图如图1 所示。

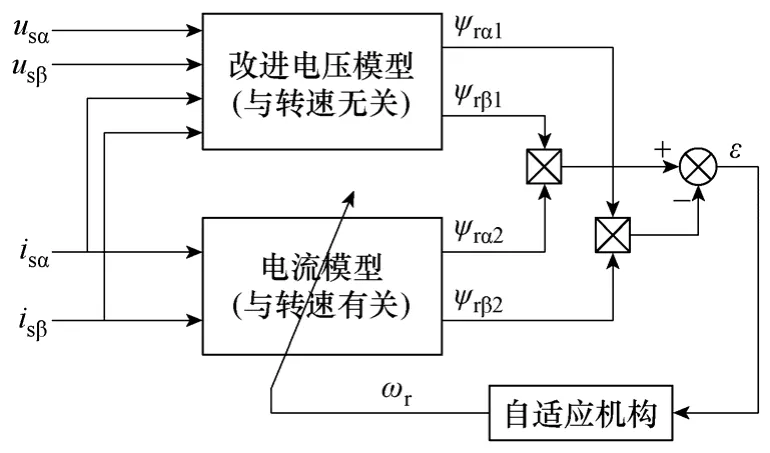
图1 基于MRAS的转速估算原理框图Fig.1 Speed estimation structure based on MRAS

图1 中，MRAS的自适应律输入量为误差ε=ψrα2ψrβ1-ψrβ2ψrα1，输出的转速辨识值ωr反馈至电流模型实现闭环控制。根据ε不断调制ωr，直到误差ε为零，转速辨识值也就达到了真实值；如果ε不为零，说明转速估计值和实际转速不一致。显然，转速估计偏差与两个模型的转子磁链误差间有必然的联系，即图1 中的自适应机构，就是要根据可调模型与参考模型间的状态矢量偏差通过自适应机构的调制，使可调模型的转速估计值能逼近转速的实际值。

3 传统MRAS 转速估算方法的问题

MRAS 采用的参考模型为电压模型，从式（1）可以看出，电压模型法的转子磁链观测器实质是一个纯积分器，其优点是：①算法简单；②算法不含转子电阻，因此受电机参数变化影响小；③不需要转速信息，对于无速度传感器颇具吸引力。但是，定子电阻压降、纯积分环节等问题使得电压模型的使用存在一定的局限。

3.1 低速时，定子电阻变化

电机参数中，由于电机的温升，定子电阻会发生变化，假设定子电阻变化量为ΔRs，经过推导，可以得到定子磁链观测值的稳态误差与ΔRs定子电阻偏差值的关系，如式（3）所示。

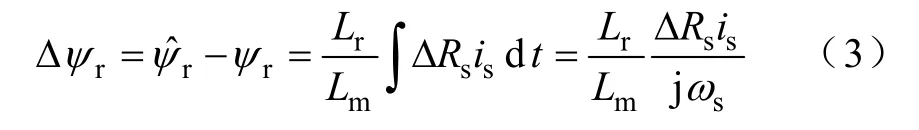
由式（3）可以看出，当定子电阻存在偏差时，定子磁链观测值的稳态误差与定子电阻偏差值成正比，与同步速成反比。因此，在低速条件下，转子磁链矢量估计对定子电阻的变化敏感，对于MRAS的辨识结果影响很大，此时，定子电阻的偏差不可忽略。

3.2 纯积分环节的积分初值和直流偏置

对一个纯积分环节，当输入为正弦信号时，只有在正弦信号的峰值点开始积分，积分初值才为零，否则输出信号含有直流分量；而且，当输入值含有直流偏置时，纯积分环节的输出波动较大，甚至会导致系统不收敛，这对低速时的影响尤为明显。

4 基于双参数模型参考自适应的感应电机无速度传感器矢量控制

本文提出了一种基于双参数模型参考自适应的感应电机无速度传感器矢量控制策略，将传统的模型参考自适应结构进行改进，在保持原来MRAS 系统的基础上，新建立一个MRAS 系统，把原来的可调模型当作参考模型，原来的参考模型当作可调模型来实现定子电阻的辨识，这就构成了双参数模型参考自适应系统，可以同时进行转速和定子电阻辨识，能够有效削弱低速时定子电阻变化对系统的影响，提高了系统的低速性能，结构如图2 所示。

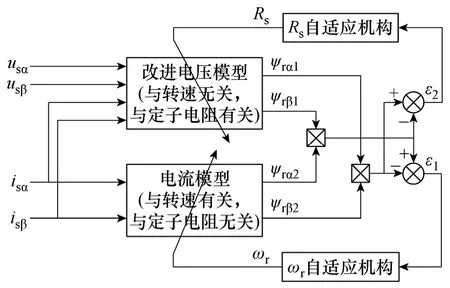
图2 基于双参数MRAS的转速估算原理框图Fig.2 Speed estimation scheme based on two-parameter MRAS

电流模型与定子电阻无关，因此将电流模型作为参考模型，将含有定子电阻的电压模型作为可调模型，利用两个模型观测的转子磁链误差构成合适的自适应率以调节可调模型参数。在改进的MRAS系统中，电压模型采用惯性环节代替纯积分环节，可以有效地解决积分初值的问题，并能有效削弱直流偏置的影响。

精确的速度估算值可以使定子电阻更快、更准确地收敛到实际值。为了实现双参数MRAS 算法，系统工作的第一个阶段为转速辨识，当估算转速已经稳定且转速指令不变时，再进行定子电阻辨识。在辨识定子电阻时，使用到的估算转速值要对实际估算值进行一阶滤波，且滤波时间较大，从而保证转速值的平滑稳定。当估算转速值波动较大或转速指令变化时，切出定子电阻辨识。

5 MRAS 转速估算系统稳定性分析

为了分析转速估算系统的稳定性，推导了转速闭环系统的线性化小信号模型，利用根轨迹法分析了系统的稳定性及可变参数对系统性能的影响。在分析过程中，假设定子电阻为常数，转速估算系统结构图如图3 所示。

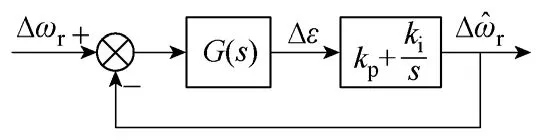
图3 转速估算系统结构图Fig.3 Structure of speed estimation system

为了推导转速估算系统的传递函数，将转子磁链模型及其估算模型在dq 坐标系中分别表示为式（4）和式（5）

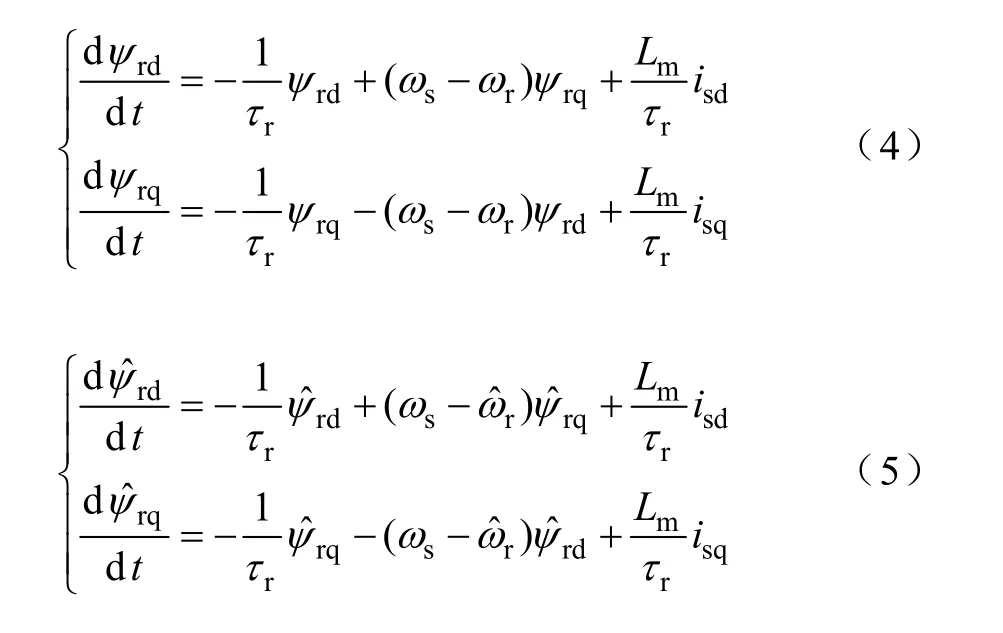
式中ψrd，ψrq——转子磁链在dq 轴的分量；

isd，isq——定子电流在dq 轴的分量。

设磁链、电流和转速的干扰量分别为Δψrd、Δψrq、Δisd、Δisq、Δωr，将其代入式（4）、式（5），消掉稳态量，可以得到系统的小信号时域模型如式（6）、式（7）所示

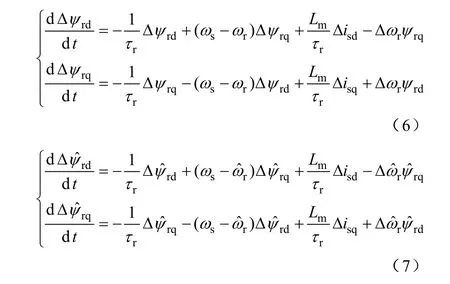
结合图2 可知，估算转速可表示为

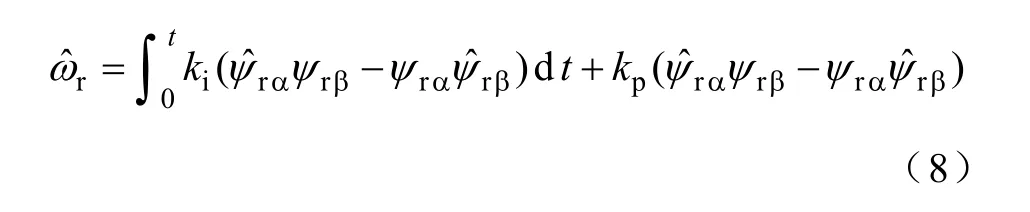
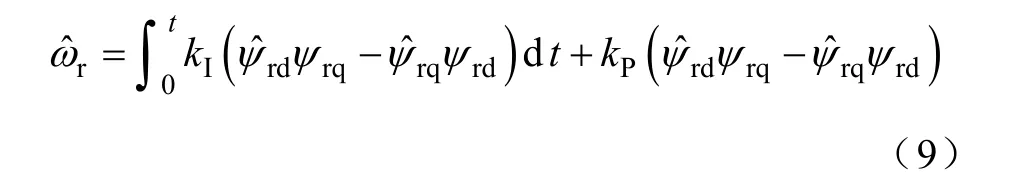
对式（6）和式（7）进行Laplace 变换，并相减整理后得到

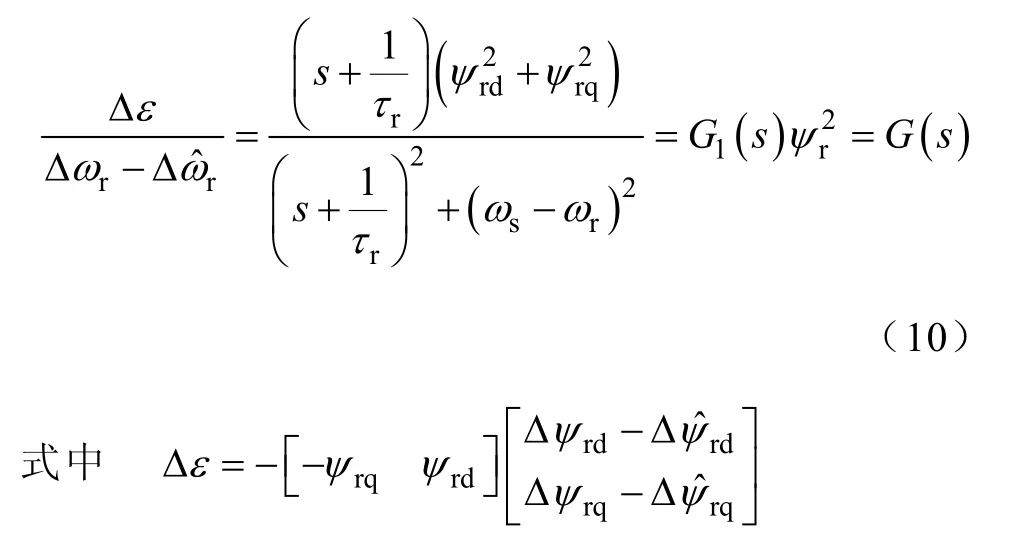
结合MRAS的转速估算原理，根据式（10）可以得到转速估算系统动态变化时的开环传递函数

由上式可以得出系统的开环零点为

极点为

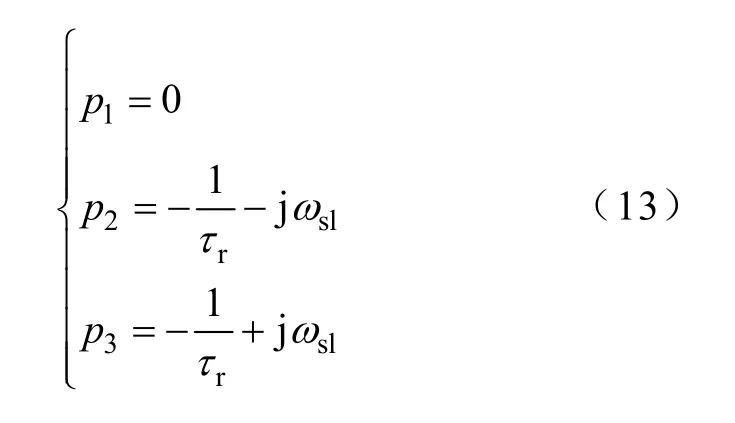
图4 给出了MRAS 转速估算系统闭环根轨迹图，由图4 可以看出，系统闭环极点都位于s 左半平面，说明转速估算系统在动态时是稳定收敛的，图中还给出了系统闭环极点位于s 平面中与负实轴成45°角附近时系统的开环增益，此时系统的平稳性和快速性较好。

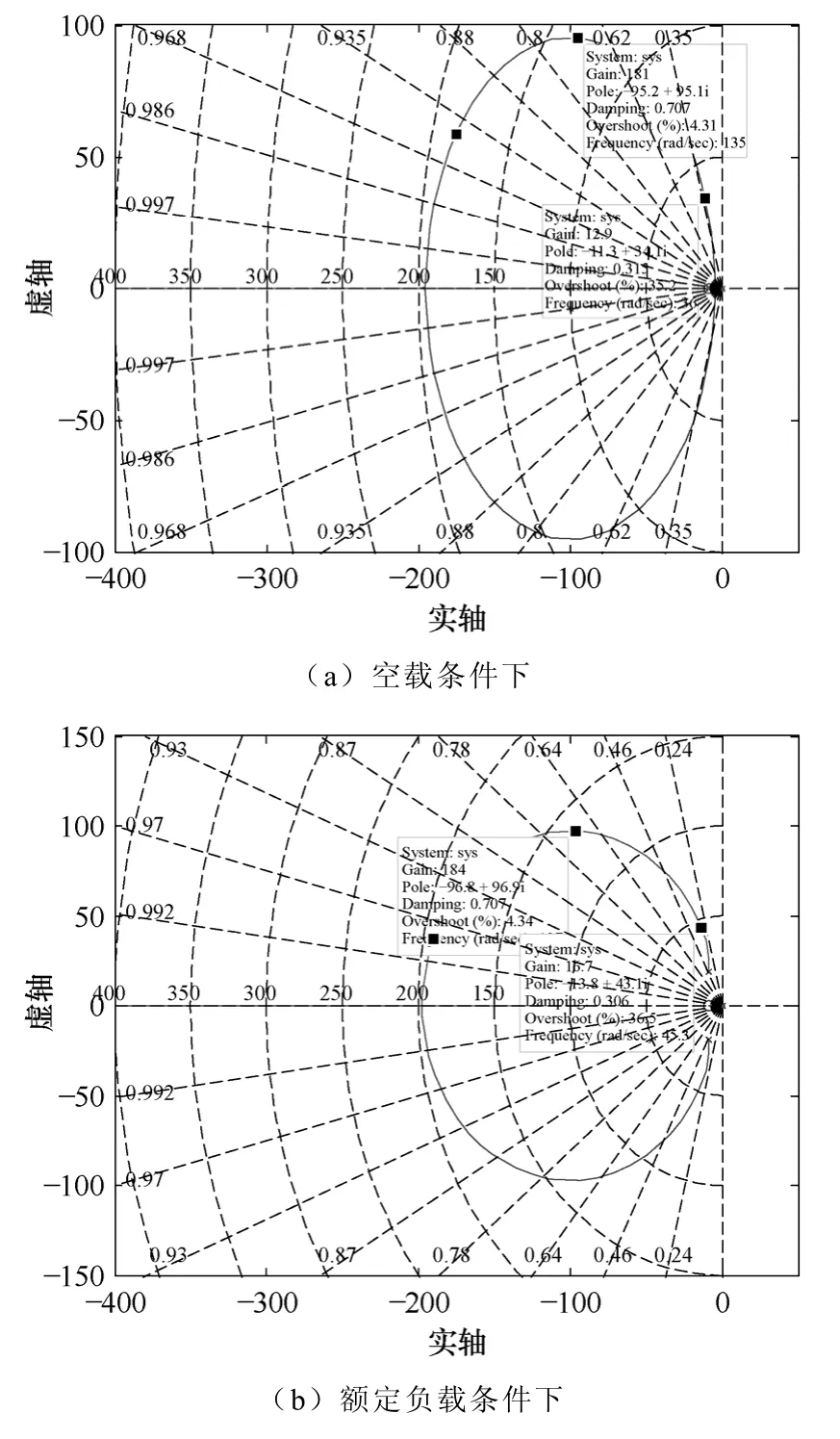
图4 转速估算系统闭环根轨迹Fig.4 Root locus of speed estimation closed system

图5 给出了转差频率在0～2 倍额定转差变化时MRAS 转速估算系统闭环根轨迹图，可以看出系统闭环极点均位于s 左半平面，而转差频率的变化对应了电机负载的变化，因此可以看出转速估算系统在全负载范围内始终是稳定的。

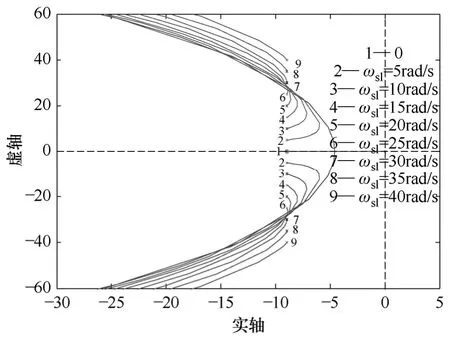
图5 负载变化时，主导极点及根轨迹图Fig.5 Root locus of closed system with load change

结合图4 给出的系统闭环极点位于s 平面中与负实轴成45°角附近时系统的开环增益，图6 给出了PI 参数变化时转速估算系统的阶跃响应曲线族，不仅分析了参数变化对系统性能的影响，同时为PI实验参数的选取提供了理论依据。图6a 为转速估算PI 调节器比例系数kp从50 到250 变化时，转速估算系统的阶跃响应曲线族。可以看出，当kp＝50，系统的超调较大，振荡次数较多，随着kp的增加超调减小，快速性较好，但是kp太大使得系统抗干扰能力变差，综合考虑选取kp＝180。图6b 为转速估算PI 调节器积分时间Ti从0.005s 到0.5s 变化时，转速估算系统的阶跃响应曲线族，可以看出，当Ti=0.02s 时系统的超调和快速性综合性能较好。

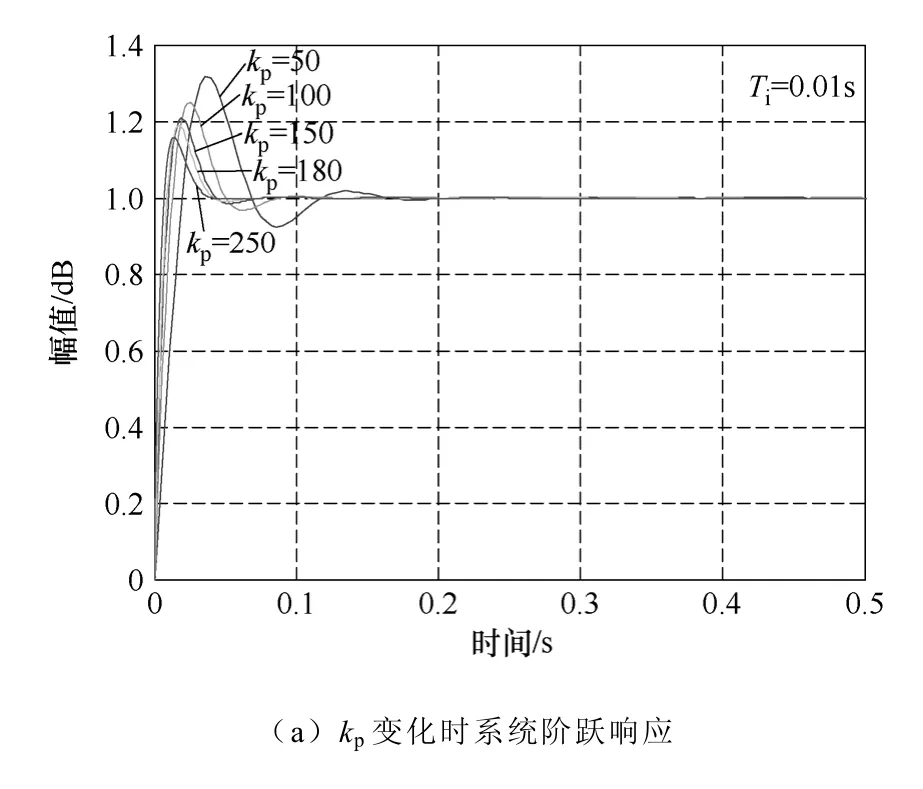
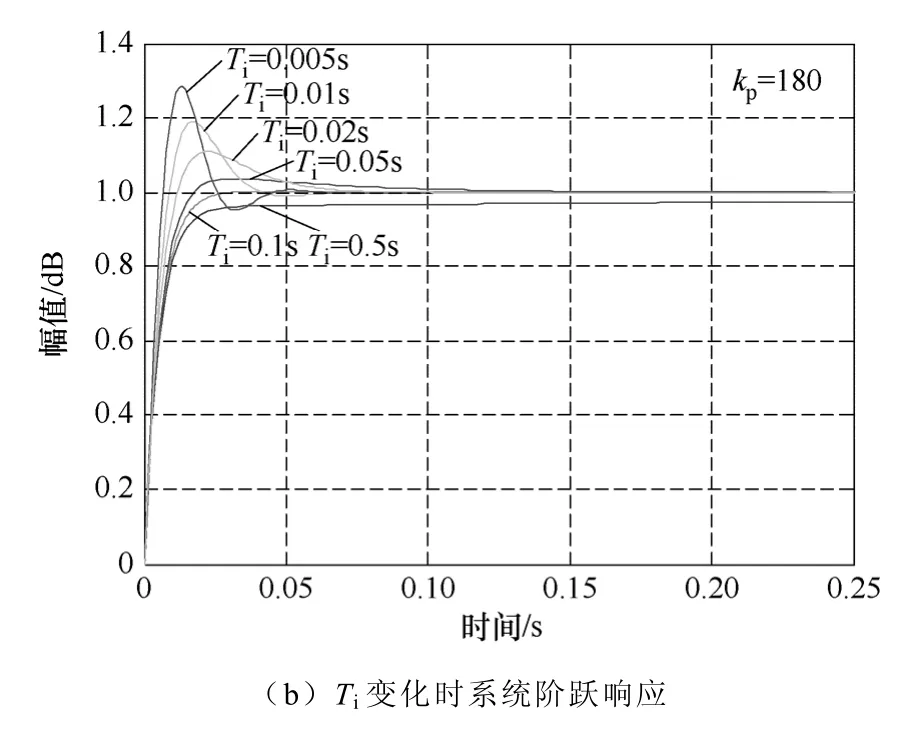
图6 PI 参数变化时转速估算系统动态响应波形Fig.6 Response of speed estimation when PI parameters change

6 实验验证

6.1 系统实现

以英飞凌XE164FM 单片机为内核搭建1.1kW实验平台，对基于双参数模型参考自适应的感应电机无速度传感器矢量控制策略进行了验证，并对系统的低速带载性能进行了实验，系统结构图如图7所示。

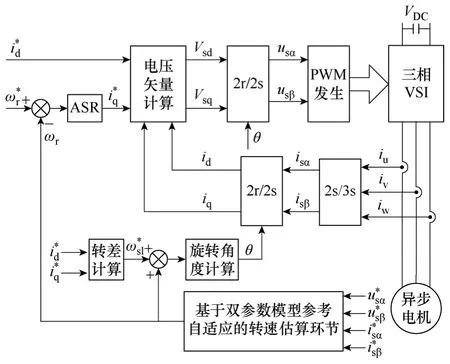
图7 基于双参数MRAS的感应电机无速度 传感器矢量控制结构图Fig.7 Structure of induction motor sensorless vector control based on two-parameter MRAS

考虑到死区效应对系统低速性能影响较大，因此，实验时对死区进行了补偿。1.1kW 感应电机参数见下表。在软件实现方面，主要包括系统初始化、主循环程序、保护中断程序Trap_interrupt、T12 下溢中断程序T12_interrupt，其中，T12 下溢中断程序是双参数 MRAS 控制的核心部分，中断周期100μs，主要完成 A-D 采样与坐标转换、双参数MRAS 算法、死区补偿、SVPWM 发生等功能。图8a 和图8b 分别给出了T12 下溢中断程序和双参数MRAS 算法子程序的流程图。感应电机参数见下表。

表 感应电机参数Tab. Parameters of induction motor

图8 主要软件流程图Fig.8 Flow chart of main software

6.2 转速估算系统稳定性分析实验验证

图9 给出了不同PI 参数下基于MRAS 转速估算方案的无速度传感器矢量控制系统，给定转速阶跃变化时估算转速的响应波形。图9a 和图9b 为Ti=0.02s 时，分别为kp=50 和kp=185 时的实验波形，可以看出kp＝50 时，估算转速的超调较大；kp＝185时，估算转速的超调减小。图9c 和图9d 为比例增益kp＝185 时，积分时间Ti为0.005s 和0.5s 时的实验波形，可以看出，当Ti=0.005s 时，估算转速的超调较大，当Ti=0.5s 时，虽然超调量减小，但是调节时间变长。比较可知，取kp＝185，Ti=0.02s 时，基于MRAS 转速估算方案的无速度传感器矢量控制系统具有较好的动态响应，与稳定性分析结果一致。

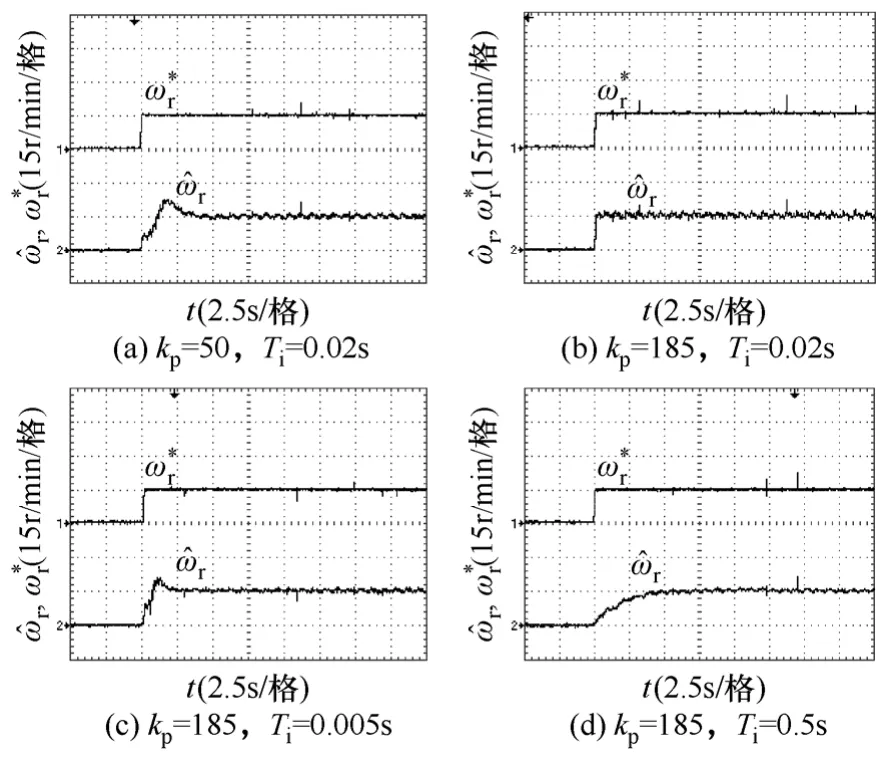
图9 不同PI 参数下给定转速阶跃变化时估算转速的波形Fig.9 Estimated speed waveforms of system with variable gains of PI

6.3 基于双参数MRAS 转速估算系统实验验证

图10 验证了基于双参数MRAS 转速估算系统的正确性。图 10a 给出了给定转速从+15r/min→+75r/min 变化时估算转速的响应波形。图10b 给出了给定转速从+15r/min →+75r/min →-75r/min →-15r/min 变化时的电流波形，从图中可以看出，估算转速能很好地跟踪给定转速。电机正反转过零切换时，电流无相位突变和振荡，可以实现正反转的平滑切换。

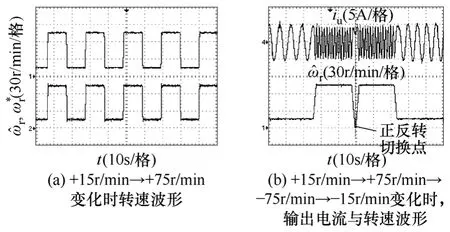
图10 基于双参数模型参考自适应的转速估算实验波形Fig.10 Experimental waveforms of speed estimation scheme based on two-parameter MRAS

6.4 低速带载性能对比实验

图11 给出了15r/min 运行时，突加180%额定负载对比实验波形。从图11a 可以看出，突加180%额定负载后，转矩电流上升，同时输出电流变大，且很快达到稳态，实测转速有降落，但很快能恢复到15r/min，说明基于双参数MRAS的无速度传感器矢量控制系统在15r/min 时能快速响应负载的变化，加载动态响应良好，15r/min 能达到180%的额定转矩。但是，图11b 表明，当采用传统MRAS 策略时，突加180%额定负载后，电机出现堵转，测试数据表明，此时系统最大只能带约150%额定负载。实验结果验证了双参数MRAS 比传统MRAS具有更好的低速带载性能。

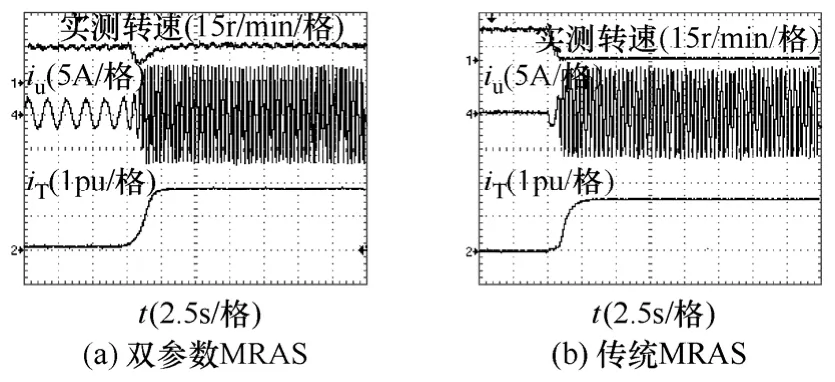
图11 15r/min 运行时，突加180%额定负载实验对比波形Fig.11 Experimental comparison waveforms of 15r/min with 180% rated load

7 结论

针对定子电阻变化和积分直流偏置导致的传统MRAS 低速带载性能不高的问题，本文提出了一种基于双参数模型参考自适应的感应电机无速度传感器矢量控制策略，可以同时进行转速辨识和定子电阻辨识。通过实验验证，双参数MRAS 算法能够有效削弱低速时定子电阻变化对系统的影响，比传统MRAS 具有更好的低速带载性能。该方法对于异步电机无速度传感器矢量控制的研究和工程应用具有一定的参考价值。

[1]Liu Xu,et al.On speed sensorless vector control system for induction motor based on estimating speed by torque current differential[C].Proceedings of the 27th Chinese Control Conference,2008:16-18.

[2]Mohamed Rashed,Fraser Stronach,Peter Vas.A new stable MRAS-based speed and stator resistance estimators for sensorless vector control induction motor drive at low speeds[C].IEEE Industry Applications Conference,2003:1181-1188.

[3]陆海峰,瞿文龙,张磊,一种基于无功功率的异步电机矢量控制转子磁场准确定向方法[J].中国电机工程学报,2005,25(16):116-120.Lu Haifeng,Qu Wenlong,Zhang Lei,et al.A novel rotor flux oriented scheme of induction motor based on reactive power[J].Proceedings of the CSEE,2005,25(16):116-120.

[4]Maiti S,Chakraborty C,Hori Y.Model reference adaptive controller-based rotor resistance and speed estimation techniques for vector controlled induction motor drive utilizing reactive power[J].IEEE Transactions on Industry Electronics,2008,55(2):594-601.

[5]Chandan Chakraborty,Ravi A V Teja,Suman Maiti,et al.A new V×I based adaptive speed sensorless four quadrant vector controlled induction motor drive[C].IEEE International Power Electronics Conference,2010:3041-3048.

[6]Ravi A V Teja,Chandan Chakraborty.A novel model reference adaptive controller for estimation of speed and stator resistance for vector controlled induction motor drives[C].IEEE International Symposium on Industrial Electronics,2010:1187-1192.

[7]Shady M Gadoue,Damian Giaouris,John W Finch.Performance evaluation of a sensorless induction motor drive at very low and zero speed using a MRAS speed observer[J].IEEE International Conference on Industrial and Information Systems,2008:1-6.

[8]Mohamed Boussak,Kamel Jarray.A high-performance sensorless indirect stator flux orientation control of induction motor drive[J].IEEE Transactions on Industrial Electronics,2006,53(1):41-49.

[9]Maiti S,Chakraborty C,Hori Y.Model reference adaptive controller-based rotor resistance and speed estimation techniques for vector controlled induction motor drive utilizing reactive power[J].IEEE Transactions on Industry Electronics,2008,55(2):594-601.

[10]Villazana S,Seijas C,Caralli A,et al.SVM-based and classical MRAS for on-line rotor resistance estimation[C].IEEE International Symposium on Intelligent Signal Processing,2007:1-6.

[11]Maria Stefania Carmeli,Francesco Castelli Dezza,Matteo Iacchetti.Effects of mismatched parameters in MRAS sensorless doubly fed induction machine drives[J].IEEE Transactions on Power Electronics,2010,24(11):2842-2851.