MIMO通信系统的检测算法研究

王进泉

（五邑大学信息学院 广东 江门 529020）

0 引言

多输入多输出（MIMO）多天线技术由于能提供更高的容量、更大的分集增益和干扰抑制性能[1]，因而成为移动通信的一种关键技术。MIMO系统接收机接收到的是在时间上和频带上相互重叠的多路信号，信号检测性算法直接影响到MIMO通信系统的性能，因此对高性能、低复杂度的MIMO检测技术的研究已经成为无线通信研究领域热点之一。

传统的MIMO检测中常用的传统算法有MIMO最大似然（ML,MaximumLikelihood）检测算法[2]、迫零（ZF，ZeroForcing）检测算法[3]、最小均方误差（MMSE，MinimumMean-SquareError）检测算法[4]，迭代算法[5－6]有Gibbs抽样、随机化搜索。本文详细阐述了这些算法的工作原理，进行了误码性能仿真和复杂度分析。

1MIMO系统模型

MIMO通信系统的模型，如图1所示：

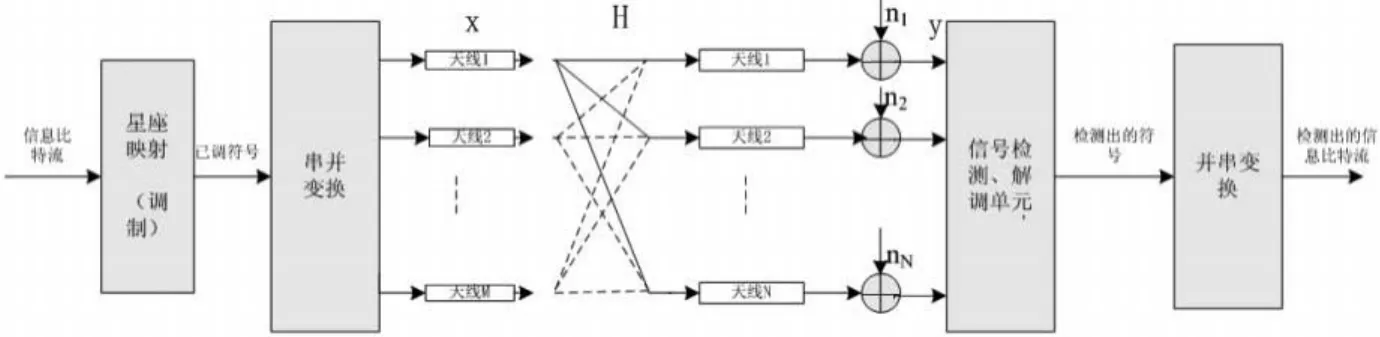
图1 MIMO通信系统模型

图1所示的MIMO系统，其等效模型表示为：

其中，M是发射天线数、N是接收天线数，且N≥M，y=[y1，…，yN]T是1×N维的接收信号，H是N×M维的信道矩阵，x=[x1，…，xM]T是1×M维的发射信号向量，xi∈Ω（i＝1，2，…，M），其中 Ω 为调制符号集合，如4-QAM 调制，有四个调制符号，组成的集合为 Ω＝{-1-i，－1＋i，＋1－i，＋1＋i}，i为虚部的表示符号。Ω集合的元素个数为。n是 1×N维的噪声。hij为矩阵H的第（i，j）项，表示从第j根发射天线到第i根接收天线的信道增益，服从瑞利分布。x为各项独立同分布。n为各项独立同分布且服从均值为零，方差为的复高斯分布。

1 传统检测算法

1.1 最大似然（ML）检测算法

这是理论最优的检测算法[2]，能够完全获得接收分集增益。但是在实际应用中，由于该算法在检测过程中要涉及到所有可能的发射向量，导致其计算复杂度太高，与调制阶数和发射天线数呈指数关系。最大似然检测算法的公式为：

其中，‖·‖2为向量的二范数，ΩM为发送端的采取的调制星座中所有的发送符号的星座集合。

（2）式求得的x向量就是最佳向量，是发射符号向量的最佳估计。由（2）式可知，欲求得最佳向量，需进行穷搜索，需要搜索次，可见，其复杂度是随着发射天线数量的增加而成指数增长。在高阶调制和发射天线较多时，难以实时实现检测。

1.2 迫零（ZF）检测算法

迫零算法[3]是常用的检测算法。该算法属于线性检测算法，就是用一个线性滤波器来分离混叠信号。当信噪比（SNR）比较低时，会放大噪声，不利于实际应用。

迫零算法：

1.3 最小均方误差（MMSE）算法

最小均方误差[4]算法也是常用的检测算法之一，也属于线性检测算法。由于该算法考虑到了噪声对信号的影响，所以性能较ZF算法有所提高。

MMSE算法：

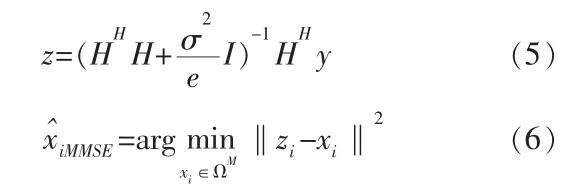
MMSE算法可以认为是一种广义的ZF算法，它平衡了信号间干扰以及噪声所带来的影响，从而使信号与干扰信号以及噪声的比值（干噪比）变大。

2 迭代检测算法

将复数形式的（1）式变换为实数形式，作如下变换

其中，R（*）和 I（*）分别表示变量的实部和虚部，（*）T表示矩阵的转置。通过（7）～（10）式的变换，可将复数模型（1）式转化为实数模型：

2.1 Gibbs抽样检测算法

基于马尔科夫链-蒙特卡罗（MCMC，MarkovchainMonteCarlo）的方法已经在CDMA和MIMO中获得应用[7－8]。在MCMC方法中，通过马尔科夫链-蒙托卡罗仿真可以获得MIMO系统的统计特性。可以通过使用MCMC仿真来解决MIMO信号的检测问题。其复杂度较低。Gibbs抽样算法就是基于MCMC的一种算法，它是从多维概率分布中根据一定的抽样规则来计算的。

在MIMO系统信号检测中，联合概率分布函数为：

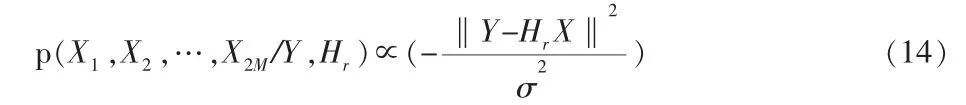
在传统的Gibbs抽样算法中，算法是从一个初始向量开始的，初始向量记为X（t=0）。 在每次迭代中，根据以下规则来更新：

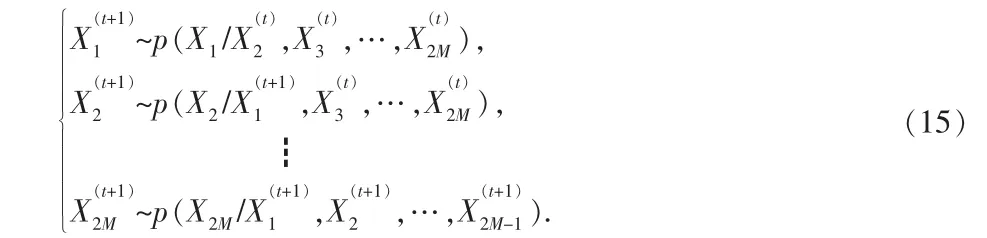
其中t为迭代次数。在所有的迭代中，找出能使ML成本函数最小的符号向量，该符号向量就是所求的检测符号向量。

在文献[5]中的所提出的MCMC算法的联合分布函数为

α是一个参数，α的选择，在文献[5]中已说明。在每次迭代中该参数是固定的。

2.2 随机搜索（RS，RandomizedSearch）算法

RS算法在文献[6]中有介绍，这一节将阐述RS算法，RS算法的一个关键因素就是搜索步骤，是使用随机选择的方法去在相邻搜索中寻找候选信号向量。RS算法是迭代算法，下面将具体阐述这个算法：

在给定Y和Hr的前提下，RS算法开始于初始信号向量X（t=0），一个固定的索引集合 S=（1，2，…，2M），两个动态的索引集合 C和D，其中C和D初始是空集合。在每次迭代中，集合C只被更新一次，而集合D被更新多次（或不被更新）。C将存放每次迭代中能使ML成本函数比前次迭代最小的符号位置索引号（如1，2，3，…，2M）。换句话说，即在第t次迭代，能使ML成本函数最小的X（t）的元素的位置索引号，此索引号将被加到集合C中，成为C的一个元素。D将包含在本次迭代中，不能使ML成本函数改善的符号的位置索引号。

X（t）的相邻集合，记为 N（X（t）），如下：

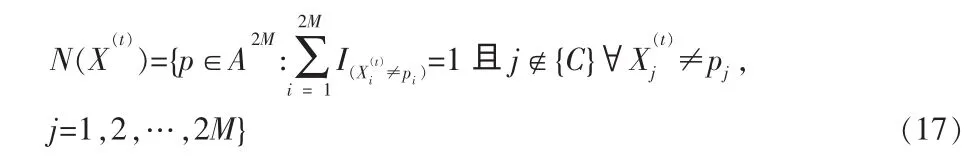
RS算法的步骤如下：

（1）给定初始方案向量 X（t＝0），找到它的相邻集合 N（X（t＝0））。

（2）从索引集合{S-C-D}中随机选择一个元素，记为m。从向量集合 N（X（t））中选择一个子集，记为{d（j），j=1，2，…，－1}，d（j）不同于X（t）中的第 m 个元素，m∈{S-C-D}。 令 g（X（t）→d（j））作为 X（t）与 d（j）之间ML成本函数的差异函数，如下：

其中，zm是z的第m个元素，Gi，j为矩阵G的第i行第j列的元素。

步骤三：计算

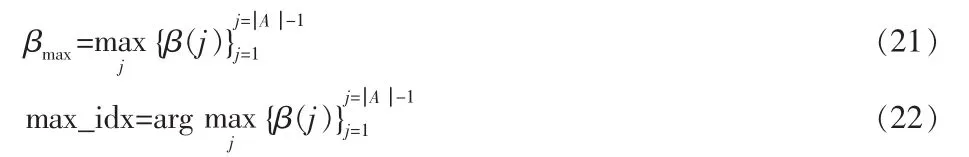
βmax有两种情况

当 βmax≥0 时：

此时，t=t+1，X（t）=d（max_idx），把 m 加入到集合 C 中，找出此时最新的相邻集合 N（X（t）），如果 C≠S 时，回到步骤二；否则 X（t）作为最终结果输出并终止算法。

当 βmax＜0 时：

此时，把m加入到集合D中，如果D≠{S-C}时，回到步骤二；否则X（t）作为最终结果输出并终止算法。

RS算法的步骤如上所诉，本算法的中的初始向量可以自由选择，也可以结合其他算法选择初始向量，如ZF,MMSE。RS算法的复杂度为 O（M1.4）[2]。

3 性能仿真与复杂度分析

3.1 误比特率性能

本节通过c++仿真，对本文中介绍的几种检测算法进行误比特率（BER）性能仿真和分析。假设信道是平坦瑞利信道，接收端已知信道状态信息。

图2给出了采用4-QAM调制，发射天线数为4，接收天线数为4。 0～20dB 信噪比条件下分别应用 ML、ZF、MMSE、Gibbs抽样、RS五种检测算法进行信号检测的BER性能曲线仿真图。由图2所示，为各种检测算法的误比特率的仿真图，从图中可以看出最大似然检测性能最佳，迫零检测算法的性能最差。在BER=10-2时，最优算法ML的SNR=8dB，最差的算法ZF的SNR=20dB，SNR相差 12dB，ML与Gibbs抽样检测算法相比较，SNR相差6dB，ML与RS检测算法相比较，SNR相差6.5dB.

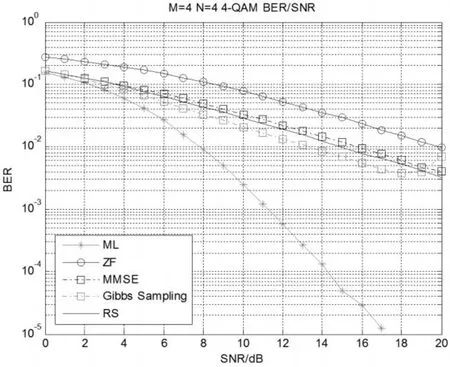
图2 各种算法的误比特率仿真图

3.2 复杂度分析

性能最优的ML检测算法的复杂度是一个指数形式，算法的复杂度随着发射天线数和调制阶数呈指数增长，其复杂度参考文献[2]。ZF算法的复杂度见文献[3]，MMSE的复杂度参考文献[4]，Gibbs抽样的复杂度见文献[5]，RS的复杂度参考[6]。现将这几种算法的复杂度列举如下，见表1。

4 结束语

MIMO是无线通信领域的一种关键技术，可提供高的系统容量。但其信号检测难度远高于传统单输入单输出系统。从MIMO系统的信号检测出发，本文介绍了MIMO系统的传统检测算法和迭代算法，并对这些算法进行了BER性能分析和复杂度分析。通过总结和比较，认识了主要算法的优缺点。按性能的优劣来看，ML的误比特率最低，性能最好但其复杂度最高，为折中起见，RS算法的的误比特率较低，其复杂度也较低，便于在实际的系统中应用。

表1 各算法的复杂度

［1］I.E.Telatar.Capacityofmulti-antennaGaussianchannels [J].EuropeanTrans.Telecommun,Vol.10,No.6,pp.585-595,November1999.

［2］W J Choi,R Negi,J M Cioffi.Combined ML and DEF decoding for the VBLAST system [A]//IEEE International Conference on Communication,vol.3[C].2000:1243-1248.