收敛无穷限广义积分被积函数在无穷远处性质
张立柱
(上海财经大学应用数学系,上海 200433)
收敛无穷限广义积分被积函数在无穷远处性质
张立柱
(上海财经大学应用数学系,上海 200433)
讨论了第一型广义积分收敛时被积函数在无穷远处渐近性质,证明当广义积分收敛时,被积函数在无穷远处不一定趋于零,而可以表现为其他多种形式,如剧烈振荡的连续函数,或间断函数,甚至可以是特殊形式的非负连续函数等.最后给出当广义积分收敛时,判别被积函数在无穷远处是否趋于零时的几个条件.
广义积分;渐近性质;收敛
1 引言


从几何意义上讲,积分可理解为函数曲线与x轴所围图形面积的代数和.从sin x2的图像可看出(图1),当x充分大时,函数剧烈震荡,可以近似理解为,此时无论如何选取积分区间,被积函数与x轴所围正的面积与负的面积可以相互抵消,从而导致广义积分收敛.
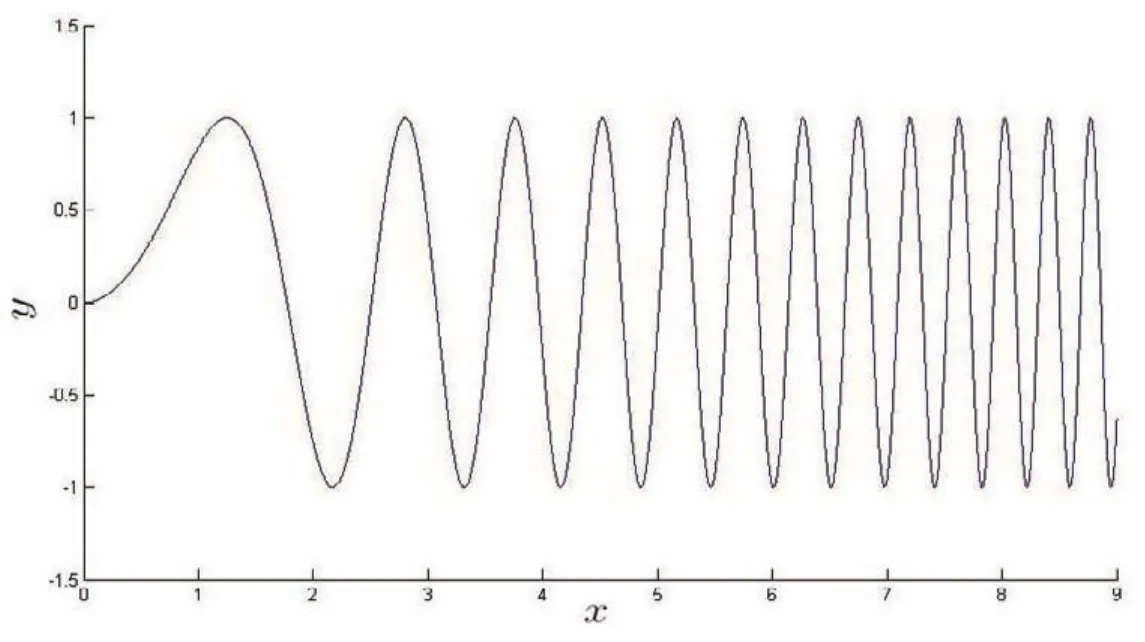
图1 函数y=sin x2的图像
由此而引发的一个很自然的想法,如果广义积分收敛,同时排除上面这种会导致正负面积抵消的函数出现,即限定广义积分不仅收敛,而且是绝对收敛的,是否就会有limx→+∞f(x)=0呢?答案依然是否定的.定义函数
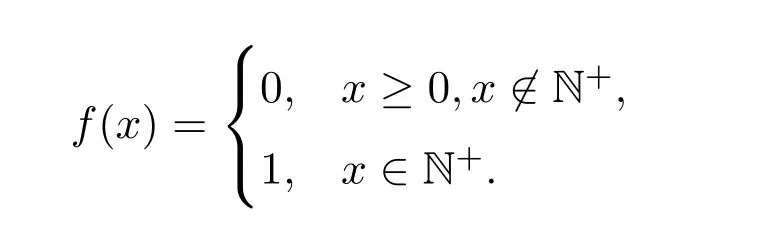
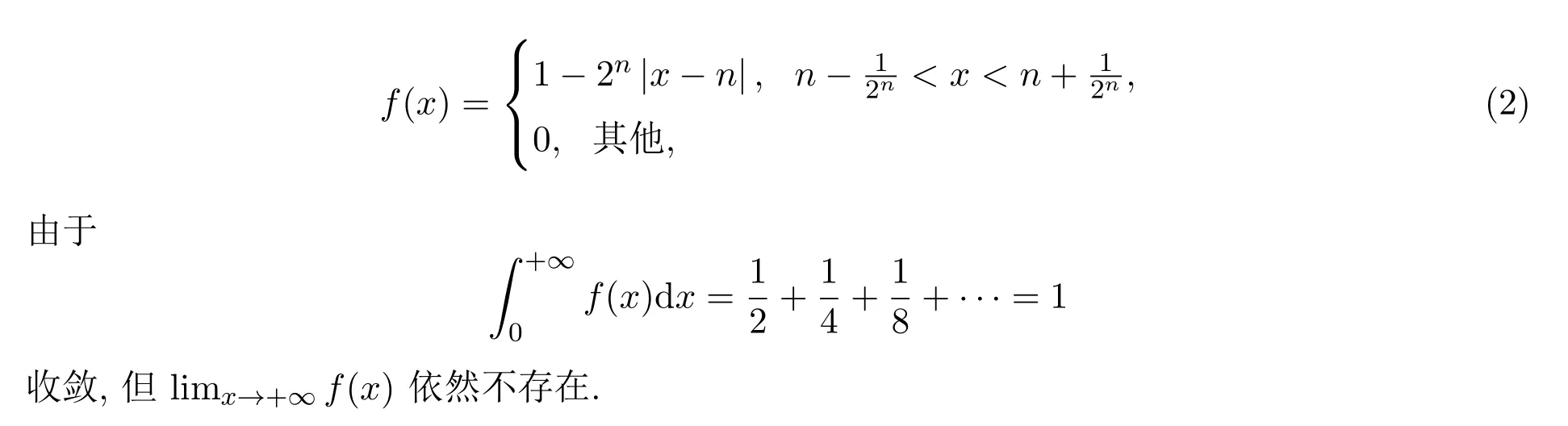
在区间[0,+∞)中的绝大部分里都有f(x)=0(如图2所示),只有总和不超过2的区间里才有f(x)>0,看起来似乎是由于f(x)>0的区间段过小导致积分收敛,如果针对这一点,将函数再修正为在整个积分区间上都有f(x)>0,此时应该会有limx→+∞f(x)=0了吧?答案依然是不能.考察函数
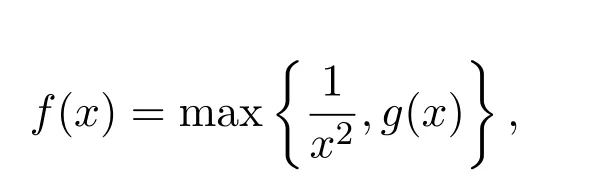
这里函数g(x)是按公式(2)定义的.显然在区间[1,+∞)上f(x)>0连续.再由
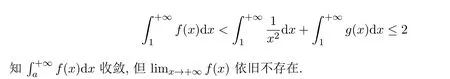
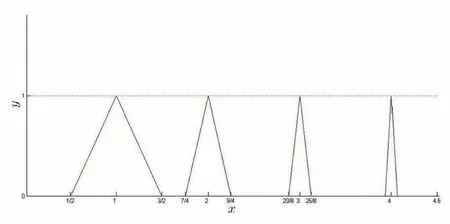
图2 (2)式定义的函数图像
2 ∫+∞af(x)d x收敛时使得limx→+∞f(x)=0成立的条件
以上反例的一个共同点是,当x充分大时,函数总有“震荡点”存在,这些“震荡点”对广义积分收敛影响不大,但却会影响函数在无穷远处的性质,这就是广义积分与无穷级数的一个很重要的区别.下面研究如何消除这些“震荡点”的影响.
定理2.1若∫+∞af(x)d x收敛,且f(x)单调,则

证明不妨设f(x)单调减少,则此时必有f(x)≥0.否则设存在x0使得f(x)<0,由f(x)单调减少知,∀x>x0有f(x)<f(x0)<0,根据广义积分比较判别法知积分发散,从而与题设矛盾.
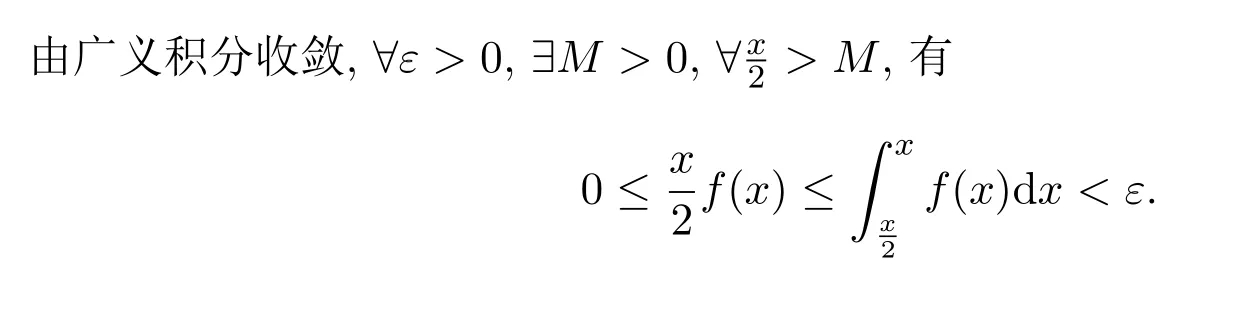


[1]殷承元.数学分析(下)[M].上海:上海财经大学出版社,2005.
[2]陈纪修,於崇华,金路.数学分析(上)[M].北京:高等教育出版社,2004.
[3]谢惠民,韫自求,易法槐,等.数学分析习题课讲义(上)[M].北京:高等教育出版社,2003.
[4]裴礼文.数学分析中的典型问题与方法[M].2版.北京:高等教育出版社,2006.
[5]程希旺.收敛无穷限反常积分被积函数在无穷远处的极限[J].安庆师范学院学报,2006,12(1):40-45.
[6]连丹青.关于的收敛性与的关系[J].湖南民族学院学报,2008,26(4):386-388.
Asymptotic properties of convergent in finite integral′s integrand
Zhang Lizhu
(Department of App lied Mathematics,Shanghai University of Finance and Econom ics, Shanghai 200433,China)
In this paper,asym ptotic properties of convergent infinite integral′s integrand are discussed.It is proved that the lim itation of integrand at infinite distance does not equal zero when the in finite integral is convergent,but the integrand can bem any other types,such as violent vibrating continuous function,discontinuous function,or even non-negative continuous function of specialized type.Several conditions are given to distinguish whether the lim itation of integrand at in finite distance equals zero or not when the in finite integral is convergent.
infinite integral,asym p totic p roperty,convergence
O172.2
A
1008-5513(2012)03-0303-05
2011-07-02.
张立柱(1973-),博士,讲师,研究方向:计算流体力学.
2010 MSC:26A 42

