弱耗散抽象发展方程全局吸引子的存在性

王春梅,汪璇,钟承奎

(1.西北师范大学数学与信息科学学院,甘肃兰州 730070;2.南京大学数学系,江苏南京 210093)

弱耗散抽象发展方程全局吸引子的存在性

王春梅1,汪璇1,钟承奎2

(1.西北师范大学数学与信息科学学院,甘肃兰州 730070;2.南京大学数学系,江苏南京 210093)

采用定义泛函,忽略粘性阻尼项时,在特定空间中研究了弱耗散抽象发展方程,得到了该方程全局吸引子的存在性结论,丰富了该类方程全局吸引子存在性的证法.

弱耗散抽象发展方程;记忆核;全局吸引子

1 引言

在有界域Ω⊂ℝ3上考虑弱耗散抽象发展方程

全局吸引子的存在性,其中参数θ∈(0,2],k(0),k(∞)＞0,且k′(s)≤0,∀s∈ℝ+.

关于通常的抽象发展方程:

系统能量耗散通过阻尼项和记忆项实现,而我们研究的方程(1)在该方程基础上去掉阻尼项,则能量耗散减弱.由于去掉阻尼项,通常的抽象发展方程能量估计方法在此方程上无法直接使用,具体表现在能量估计中将无法用ut+σu作为试验函数来进行能量估计.本文通过定义泛函巧妙地克服了这项困难.

关于忽略粘性阻尼项的双曲方程前人已有所研究,并获得了全局吸引子的结果[1].但当算子为抽象算子时,关于忽略粘性阻尼项的抽象发展方程的讨论还很少.关于方程(1),本文研究了弱解的存在唯一性,并且,进一步证明了方程(1)对应的解半群的全局吸引子的存在性.

2 预备知识

设H=L2(Ω),b(u,v)为H上的连续的双线性型,且是对称和强制的.由此线性型联合H上的线性自伴无界算子A,其定义域D(A)⊂H,令(Au,v)=b(u,v),∀u,v∈H.设{λj}j∈ℕ,{ωj}j∈ℕ为A的特征值和特征向量,因此{ωj}j∈ℕ可构成H中的一组正交基,有

使用这组基可容易定义A同构的幂算子族Aθ,θ∈(0,2][2],其定义域D(Aθ)⊂H.显然

为Hilbert空间,内积和范数相应为:

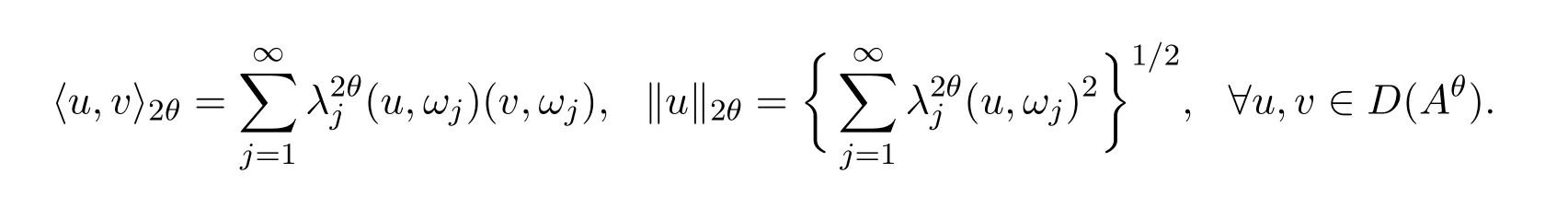
易知算子Ar为从D(As)到D(As-r)上的同构映射,∀s,r∈ℝ.

由A的无界自伴性知Aθ也为无界自伴.因此当θ1≥θ2时,D(Aθ1)在D(Aθ2)中紧,则

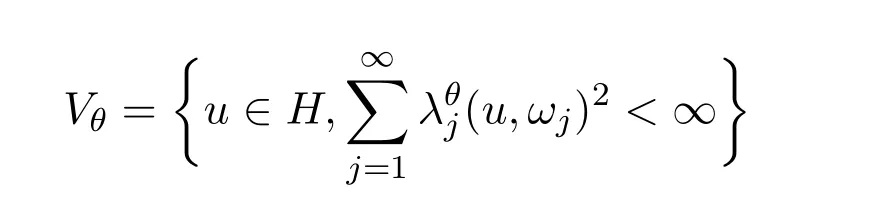
3 主要结果

[1]GiorgiC,Rivera JE M,Pata V.Global attractors for a sem ilinear hyperbolic equations in viscoelasticity[J]. J.Math.Anal.App l.,2001,260:83-99.

[2]Teman R.In finite Dimensional Dynam ical System in Mechanics and Physics[M].2nd ed.New York:Sp ring-Verlag,1997.

[3]Pata V,Zucchi A.A ttractors for a dam ped hyperbolic equation with linear m em ory[J].Adv.Math.Sci. App l.,2001,11:505-529.

[4]汪璇,任利宁.带衰退记忆的抽象发展方程全局吸引子的存在性[J].兰州大学学报:自然科学版,2008,44:99-102.

[5]汪璇,钟承奎,马巧珍.带衰退记忆的抽象发展方程解的渐近性[J].西北师范大学学报:自然科学版, 2009,45:6-10.

[6]Ma Qingfeng,Wang Shouhong,Zhong Chengkui.Necessary and sufficient conditions for the existence of global attractor for sem igroup and app lication[J].Indiana University Mathem atics Journal,2002,51:1541-1559.

[7]Ma Qiaozhen,Zhong Chengkui.Existence of strong global attractors for hyperbolic equation with linear memory[J].App lied Mathematicsand Com putation,2004,157:745-758.

[8]Ghidaglia JM,Tem am R.A ttractors for dam ped nonlinear hyperbolic equations[J].J.m ath.pures App l., 1987,66:273-319.

[9]汪璇,钟承奎.带衰退记忆的抽象发展方程强全局吸引子的存在性[J].兰州大学学报:自然科学版, 2010,46:113-118.

Existence of global attractors for weak d issipation abstract evolution equations

Wang Chunmei1,Wang Xuan1,Zhong Chengkui2
(1.College of Mathem atics and In form ation Science,Northwest Norm al University,Lanzhou 730070,China; 2.Departm ent of Mathem atics,Nanjing University,Nanjing 210093,China)

In this paper,by themethod of defining functional,when viscoelastic dam ped term wasneglected,we investigated and achieved the existence of global attractors for weak dissipation abstract evolution equations in particu lar space,so that them ethod of the existence of globalattractors for this type of equationswas extended.

weak dissipation abstract evolution equation,memory kernel,global attractor

O175.27;O175.29

A

1008-5513(2012)03-0401-11

2012-01-12.

国家自然科学基金(11101335,10871160).

王春梅(1987-),硕士生,研究方向：无穷维动力系统.

2010 MSC:38Q 80