关于Brown随机指数一致可积性条件的推广

李军

(西北师范大学数学与统计学院,甘肃 兰州 730070)

关于Brown随机指数一致可积性条件的推广

李军

(西北师范大学数学与统计学院,甘肃 兰州 730070)

利用Brown运动的下函数,推广了随机指数一致可积性的判定条件,进而改进了Novikov条件和Kazamaki条件.

随机指数;指数鞅的一致可积性;Brown运动的下函数;Novikov条件; Kazamaki条件

1 引言及主要结果

则结论依然成立.之后,文献[4]证明了在(2)式中,取ε=0,即

蕴含条件(1).文献[5]给出了一个更漂亮的条件:

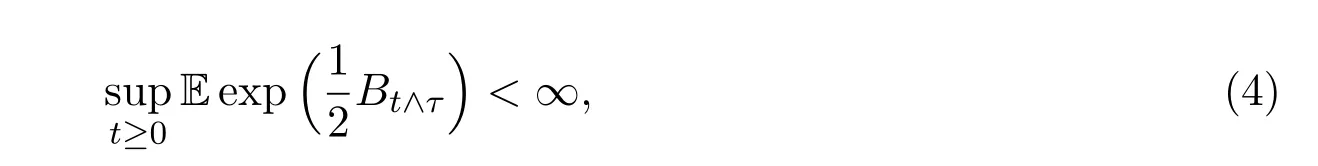
这个条件对于条件(1)是充分的,而且要比条件(2)弱.

对于条件(3)的弱化还可以采取其它方法.在文献[6-7]中,假设存在Brown运动的一个下函数φ(关于下函数的定义详见本文第二节),使得

那么条件(1)成立.文献[8]也用类似于(5)式的条件对Kazamaki条件(4)进行了弱化.文献[9]也给出了(1)式的充分条件,即

上述两个条件(6)和(7)在改进了文献[6-8]的结果的同时,特别地进一步对Novikov条件(3)和Kazamaki条件(4)式作了改进.

本文的主要工作是借助于 Brown的下函数对文献 [9]中的结果进行推广,将条件 (6)和(7)统一起来,进而得出条件(1)的更一般的条件,从而更进一步改进了Novikov条件(3)和Kazamaki条件(4).下面给出本文的主要定理.

定理1.1 令φ是Brown运动的一个下函数,则下述条件对于(1)式是充分的,即

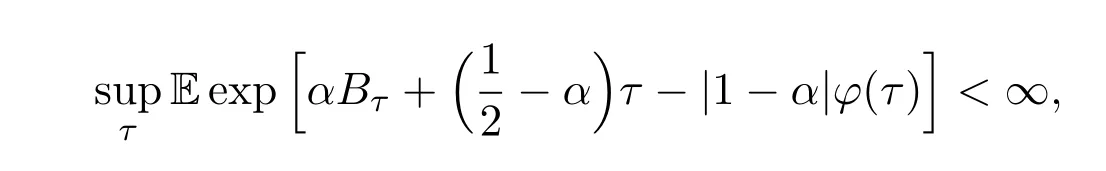
其中α∈R且α̸=1,同时,上确界是取遍所有停时τ而得到的.

2 预备知识

首先给出 Brown运动的下函数的定义[9-10].设 (Bt)t≥0是标准 Brown运动且 φ是定义在 R+上的实值连续函数.集合 A={ω:∃t=t(ω),∀s≥t,Bs(ω)＜φ(s)}属于 σ-代数X=∩t＞0σ(Bs;s≥t).由Blumenthal 0-1律可得P(A)=0或1.

注 集合A也可以表示成:A={ω:Bt＜φ(t),t→∞}.

定义2.1 若P(A)=0,则称φ是Brown运动的下函数;若P(A)=1,则称φ是Brown运动的上函数.

3 主要结果的证明

参考文献

[1]Girsanov IV.On transform ing a certain class of stochastic processes by absolutely continuous substitution ofm easures[J].Theor.Prob.App l.,1960(5):285-301.

[2]G irsanov I I,Skorohod A V.Stochastic Diff erential Equations[M].Berlin Heidelberg:Spinger-Verlag,1972.

[3]Liptser R S,Shiryaev A V.On absolute continiuty ofm easures associated with processes of diff usion type with respect to theW iener m easure[J].Izv.A.N.USSR,Ser.M ath.,1972,36:847-889.

[4] Novikov A A.On an identity for stochastic integrals[J].Theory of Probability and Its App lications, 1972,17:717-720.

[5]Kazamaki N.On a prob lem of Girsanov[J].Tˆohoku Math.J.,1977,29:597-600.

[6]Novikov A A.On the conditions of the uniform integrability of the continuous nonnegativem artingales[J]. Theory of Probability and Its App lications,1979,24:821-825.

[7]K ry lov N V.Introduction to the Theory of D iff usion Processes[M].New York:Am erican M athem atical Society,2005.

[8]K ram kov D O,Shiryaev A N.Suffi cient conditions of the uniform integrability of exponentialm artingales[J]. Progress in M athem atics,1998,168:289-295.

[9]Cherney A S,Shiryaev A N.On criteria for the uniform integrability of Brownian stochastic exponentials[C].Optim al Control and Partial D iff erential Equations,in honour of A lain Bensoussan′s 60th birthday. Am sterdam:IOS Press,2001.

[10]Itˆo K,M cKean H P.D iff usion Processes and Their Sam p le Paths[M].New York:Springer,2010.

[11]Karatzas I,Shreve S.Brownian M otion and Stochastic Calculus[M].New York:Springer-Verlag,2006.

[12]黄志远.随机分析学基础[M].2版.北京:科学出版社,2001.

The generalization of criteria for the un iform in tegrability of B row n ian stochastic exponentials

Li Jun
(College of Mathematics and Statistics,Northwest Normal University,Lanzhou 730070,China)

In this paper,we app ly lower function of Brownian motion to generalize criteria for the uniform integrability of Brownian stochastic exponentials,and im p rove the Novikov condition and Kazam aki condition.

stochastic exponentials,the uniform integrability of exponentialm artingales, lower functions of Brownian motion,Novikov condition,Kazamaki condition

O211.6

A

1008-5513(2012)06-0839-06

2012-06-09.

国家自然科学基金(11061032).

李军(1986-),硕士,研究方向:随机分析及其应用.

2010 M SC:60J65