捕食者具阶段结构和脉冲扰动的群体防卫捕食系统

李顺异,唐兴芸,薛先贵

(黔南民族师范学院数学系,贵州 都匀 558000)

捕食者具阶段结构和脉冲扰动的群体防卫捕食系统

李顺异,唐兴芸,薛先贵

(黔南民族师范学院数学系,贵州 都匀 558000)

研究了一类捕食者具有阶段结构与脉冲扰动和食饵具有群体防卫效应的捕食系统,应用Floquet乘子理论和脉冲比较定理,获得了食饵(害虫)灭绝周期解局部稳定和系统持续生存的充分条件.通过数值例子讨论了脉冲周期,成年捕食者(天敌)的投放量和群体防卫效应系数对系统的重要作用,并揭示了系统诸如周期与拟周期振荡,混沌,吸引子突变等复杂的动力学现象.为实际的害虫管理提供了可靠的策略依据.

阶段结构;群体防卫;脉冲扰动;持续生存;混沌

1 引言

自然界中有许多种群在其生命历程中需要经历不同的生命阶段,即从幼年种群到成年种群,从不成熟到成熟,从成年到老年等.而且在其成长的各个生命阶段生理机能(出生率,死亡率,竞争率,捕食能力)有比较显著的差别.这在不同程度上影响着种群的持续生存和绝灭,考虑种群的阶段差异性是更具有实际意义的[1-3].

在捕食系统中,食饵的群体防卫效应是指当食饵种群密度足够大时它们能增强自身的集体防卫和保护能力,从而导致捕食者种群密度减小,甚至绝灭[4].此时,捕食者对食饵的捕食能力(功能反应函数),需要用非单调功能反应函数来描述.文献[5]在研究具有群体防卫的食物链系统时,提出了一类非线性功能反应函数:

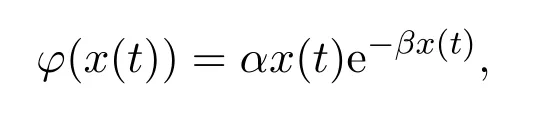
其中参数α＞0,β＞0.最近,文献[6-13]研究了脉冲作用(脉冲投放捕食者(天敌),脉冲喷洒农药等)下的捕食系统,讨论了食饵(害虫)灭绝周期解的稳定性及系统持续生存的充分条件.文献[6]构建了功能反应函数为φ(x(t))=αx(t)e−βx(t)的脉冲捕食系统,通过数值模拟揭示了诸如拟周期振荡,倍周期与半周期分支,吸引子突变,动力学行为不唯一等复杂的动力学现象.

但是,具有脉冲作用和阶段结构(无时滞)的捕食系统的研究结果较少.文献[11]讨论了捕食者具阶段结构的脉冲两食饵-捕食者系统,获得了食饵灭绝周期解局部稳定和系统持续生存的充分条件.文献[12-13]研究了捕食者具阶段结构和Holling-II功能反应的脉冲捕食系统,获得了食饵灭绝周期解全局稳定和系统持续生存的充分条件,并通过数值模拟讨论了脉冲捕食者投放量对系统动力学行为的影响.本文在捕食者种群中引入阶段结构,考虑脉冲投放捕食者(天敌)且食饵(害虫)具有群体防卫效应的的捕食系统:

2 预备引理

3 灭绝性与持续生存性

4 数值例子

在系统 (1.1)中,令a=3.5,b=1.1,α=1.2,β=0.2,k=0.75,d1=0.25,d2=0.18, m=0.5,q1=0.2,q2=0.5,初值X(0)=(0.1,0.3,3.0).由定理3.1知,当T=1.19＜Tmax≈1.2063时,食饵(害虫)灭绝周期解是局部稳定的.如图1(a)所示,食饵种群的数量在较短时间内趋于零,而捕食者种群呈稳定的周期波动.因此,为了根除害虫,并考虑到释放天敌的数量和成本,可以选择脉冲周期T使得T＜Tmax.当T=1.22＞Tmax≈1.2063时,系统(1.1)持续生存.如图1(b)所示,较少数量的食饵种群与捕食者种群以稳定的周期振荡形式共存.

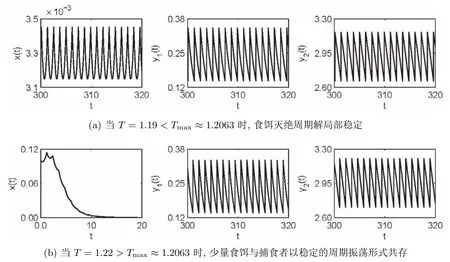
图1 系统(1.1)的动力学行为

进一步,作出系统(1.1)关于周期T在[1.2,12.2]上变化的分支图,从图2(a)可知,随着脉冲周期T的增大,系统经历了拟周期与周期振荡,混沌,吸引子突变等复杂现象,这表明脉冲周期T对系统(1.1)的动力学性质有重要的影响.在混沌区域中食饵(害虫)种群的最大值较大,而在周期区域中食饵(害虫)种群的最大值较小.在实际的害虫管理中,要根除害虫是不实际,也是不可能的.考虑到生态环境的稳定性和害虫管理的成本,可以选择适当的脉冲周期T使其略大于Tmax(如T=1.22).这样,将食饵(害虫)控制在较低的密度水平,少量食饵(害虫)与捕食者(天敌)以稳定的周期振荡形式共存.

类似地,令 T=6,除 q2外其它参数保持不变,作出脉冲投放成年捕食者的数量 q2在[0.1,3.0]上的分支图,从图2(b)可知,系统经历了混沌,周期振荡等复杂现象.投放成年捕食者的数量q2太小时,系统呈混沌形式,且食饵(害虫)种群数量的最大值较大,不利于害虫管理.由于食饵(害虫)种群数量的最大值大体上呈递减趋势,可以选择适当的成年捕食者(天敌)投放量(如q2=3.0,此时对应的Tmax≈5.9683＜T)使得少量食饵与大量天敌以稳定的周期振荡共存,达到害虫管理的目的.

令T=6,除 β外其它参数保持不变,作出群体防卫系数 β在 [0.1,2.1]上的分支图,从图2(c)可知,系统经历了周期与拟周期振荡,混沌,吸引子突变等复杂现象.随着群体防卫系数β的增大,食饵(害虫)种群的最大值大体上呈递增趋势,而捕食者(天敌)种群的数量的最大值大体上先逐渐增加,而后当β≈0.852时经历混沌吸引子突变后迅速减小,大量食饵(害虫)种群与少量捕食者(天敌)种群以稳定周期振荡的形式共存.通过以上分析可知,食饵(害虫)种群较小的群体防卫能力不能抵御捕食者(天敌)的捕食,通过脉冲投放天敌进行害虫控制是很有效的;而当食饵(害虫)具有较大的群体防卫能力时,可以在一定程度上抵御捕食者(天敌)的捕食,使得食饵(害虫)种群数量维持在较高水平.即食饵(害虫)种群具有较高的群体防卫能力时,不利于害虫(食饵)种群的控制,此时必须增加捕食者(天敌)的投放量和提高脉冲投放的频率,以达到有效控制害虫的目的.

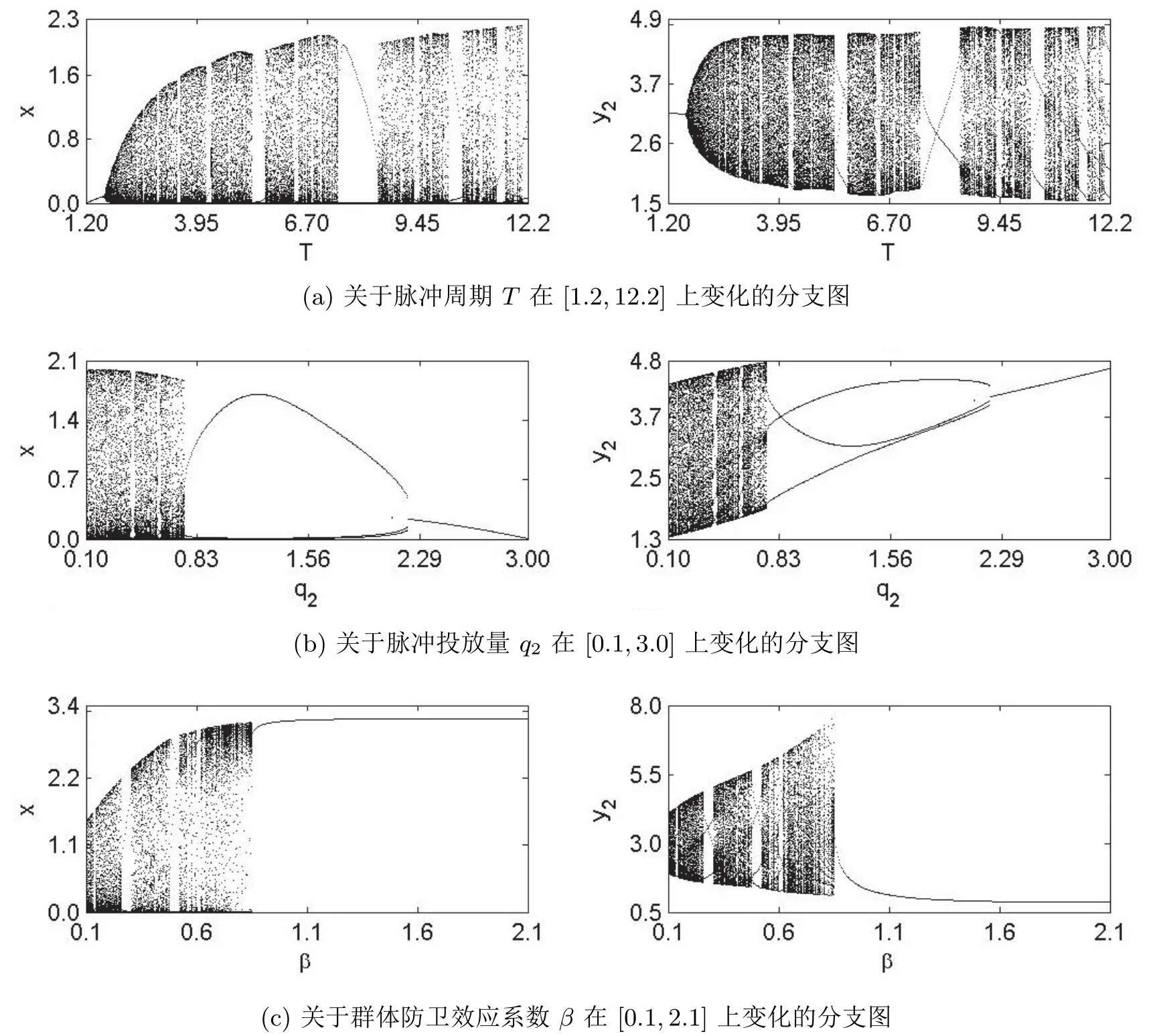
图2 系统(1.1)食饵x和成年捕食者y2的分支图

5 结论

本文研究了一类捕食者具有阶段结构和食饵具有群体防卫作用的脉冲扰动系统,通过脉冲比较定理和小扰动方法获得了食饵(害虫)灭绝周期解局部稳定和系统持续生存的充分条件,并通过数值例子佐证了定理的正确性,揭示了脉冲周期T,成年捕食者的投放量q2和食饵种群的群体防卫系数β对系统的重要作用.现实生产生活中,将害虫根除是不可能的,从生态上和经济上都是不可取的.由于Tmax是关于捕食者投放量q1,q2的函数,考虑到释放天敌的成本,以及生态环境的稳定性与生物多样性,可以选择脉冲周期T,使得T略大于Tmax,少量食饵与大量天敌以周期振荡的形式稳定共存,将害虫控制在一个可接受水平—经济危害水平之下,达到害虫管理的目的.

参考文献

[1]李顺异,熊佐亮,古仁国.一类具有阶段结构的食物链系统[J].数学的实践与认识,2008,38(13):102-109.

[2]陈丹,张耘嘉,张树文.具有巢寄生行为和阶段结构的两种群模型分析[J].纯粹数学与应用数学,2010,26(4):656-662.

[3]刘胜强,陈兰荪.阶段结构种群生物模型与研究[M].北京:科学出版社,2010.

[4]陈兰荪,孟新柱,焦建军.生物动力学[M].北京:科学出版社,2009.

[5]Freedm an H I,Ruan SG.Hop f bifurcation in three-species food chain m odelswith group defense[J].M ath. Biosci.,1992,111(1):73-87.

[6]Li SY,X iong Z L,Wang X.The study of a predator-prey system with group defense and im pu lsive control strategy[J].App l.M ath.M odel.,2010,34(9):2546-2561.

[7]任庆军,窦霁虹.具有非单调功能反应和脉冲扰动的捕食系统的分析[J].纯粹数学与应用数学,2006,22(4):444-448.

[8]陈以平,谢君辉.具有脉冲扰动和非单调功能反应的三种群捕食系统的分析 [J].纯粹数学与应用数学, 2009,25(2):332-338.

[9]张树文,张耘嘉,谭德君.具脉冲效应和Beddington-DeAnglis功能反应时滞周期捕食系统[J].纯粹数学与应用数学,2010,26(4):534-540.

[10]谭德君.具脉冲效应的非自治随机干扰的捕食-食饵系统的研究[J].纯粹数学与应用数学,2012,28(3):285-293.

[11]Song X Y,X iang Z Y.The prey-dependent consum p tion two-prey one-predatorm odelswith stage structure for the p redator and im pulsive eff ects[J].J.Theo.Biol.,2006,242(3):683-698.

[12]Wang L S,Xu R,Feng G H.A stage-structured predator-prey system with im pulsive eff ect and Holling type-II functional response[J].J.M ath.Rese.Expo.,2011,31(1):147-156.

[13]Wang L S,Xu R,Feng G H.Analysis of a stage-structured predator-prey system concerning im pulsive control strategy[J].Diff er.Equ.Dyn.Syst.,2011,19(4):303-313.

[14]宋新宇,郭红建,师向云.脉冲微分方程理论及其应用[M].北京:科学出版社,2011.

Group defense predator-p rey system with stage-structu red and im pu lsive pertu rbations on p redator

Li Shunyi,Tang Xingyun,Xue Xiangui

(Department of M athematics,Qiannan Normal College for Nationalities,Duyun 558000,China)

A p rey-predator system with group defense for p rey,stage-structured and im pulsive perturbation for predator is considered.By using Floquet theorem and com parison theorem of im pulsive diff erentialequation, the su ffi cient conditions for locally stable of prey-eradication periodic solution and permanence of the system are obtained.The im portance of the im pulsive period,the released am ount ofm ature predator and the coeffi cient of group defense eff ect are discussed by num erical exam p les,and show that the system considered has m ore com p licated dynam ics,such as periodic and quasi-periodic oscillation,chaos,attractor crisis,etc.Our results p rovide reliab le strategy basis for practical pest m anagem ent.

stage-structure,group defense,im pulsive perturbation,perm anence,chaos

O175

A

1008-5513(2012)06-0765-09

2012-09-11.

贵州省教育厅青年项目基金([2010]096);贵州省重点支持学科(应用数学)基金([2009]303).

李顺异(1982-),硕士,讲师,研究方向:非线性动力系统,生物数学.

2010 M SC:34A 37,37D45,37N25,92D25