矩阵方程AX=B的自反最小秩解及其最佳逼近

肖庆丰,胡锡炎,张磊

(1.东莞职业技术学院公共教学部,广东 东莞 523808;2.湖南大学数学与计量经济学院,湖南 长沙 410082)

矩阵方程AX=B的自反最小秩解及其最佳逼近

肖庆丰1,胡锡炎2,张磊2

(1.东莞职业技术学院公共教学部,广东 东莞 523808;2.湖南大学数学与计量经济学院,湖南 长沙 410082)

利用矩阵对的广义奇异值分解,得到了矩阵方程AX=B有自反解的充分必要件,以及有解时,定秩解、最小秩解的一般表达式.另外,给出了自反最小秩解集合中与给定矩阵的最佳逼近解.

矩阵方程;自反矩阵;广义奇异值分解;最小秩解;最佳逼近

1 引言

本文用Cn×m表示所有n×m复矩阵集合,OCn×n表示所有n阶酉矩阵组成的集合,In表示n阶单位矩阵,AH表示复矩阵A的共轭转置矩阵,A+表示矩阵A的M oore-Penrose广义逆,r(A)表示矩阵A的秩,在Cn×m上定义内积为〈A,B〉=tr(BHA),∀A∈Cn×m, B∈Cn×m,‖·‖表示由内积导出的范数,即Frobenius范数.

设P∈Cn×n,且PH=P,P2=I,则称P为广义反射矩阵.本文中的P为给定的广义反射矩阵.

设X∈Cn×n,给定广义反射矩阵P,若X满足X=PX P,则称X为关于P的自反矩阵.所有关于P的自反矩阵的全体记为:

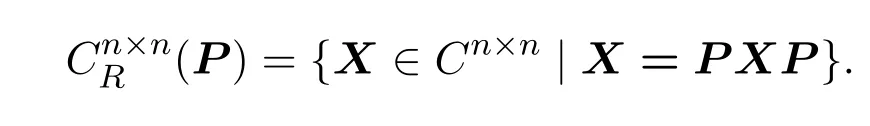
矩阵反问题是当今计算数学中一个非常活跃的研究课题,它涉及的领域有结构动力学、固定力学、物理、电学、分子光谱学、量子力学、结构设计、参数识别、自动控制等等.近年来,特殊矩阵的反问题的研究也非常活跃[1-3].关于广义自反矩阵P的自反矩阵在工程及计算科学中有很广泛的用途[4-5],文献[6]讨论了矩阵方程AX=B的自反与反自反解,但在许多应用领域,如统计学和控制论中,人们不仅需要求出矩阵方程的解,而且也需要求出具有指定秩的矩阵方程的解.文献[7]首先考虑了矩阵方程AX=B和AX B=C的定秩求解问题,文献[8]给出了矩阵方程AX=B的可能秩的解,文献[9]给出了矩阵方程AX=B最小秩的最佳逼近解.对于其他类型的矩阵方程,文献[10]使用广义逆给出了矩阵方程AX A∗=B的最大秩和最小秩的Herm itian非负定解,文献[11]使用广义逆得到了矩阵方程AX B=C的最大秩和最小秩解,文献[12]使用两次SVD得到了秩约束下矩阵方程AX A∗=B的Herm itian非负定解.本文研究矩阵方程AX=B的自反最小秩解及其最佳逼近,推广了文献[6]中的一些结果.

本文研究了如下问题:

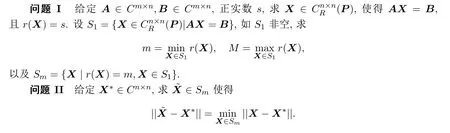
本文在第二节借助于矩阵对的广义奇异值分解,对矩阵方程CZ=D的一般解的秩进行了分析讨论,在此基础上来研究矩阵方程AX=B的定秩自反解.在第三节给出了最小秩的最佳逼近解.

2 问题 I解的表达式

其中1＞α1≥···≥αt＞0,0＜β1≤···≤βt＜1,而α2i+β2i=1,i=1,···,t.

引理 2.3 假设C∈Cm×n,D∈Cm×p,矩阵对(C,D)的广义奇异值分解如引理2.2,则矩阵方程CZ=D有解Z∈Cn×p的充要条件是r(C,D)=r(C),且若矩阵方程CZ=D有解,则有

(1)矩阵方程C Z=D的通解表达式为:

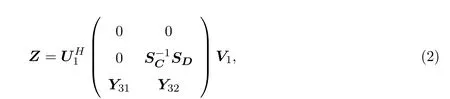
其中Y31,Y32是具有相应维数的任意矩阵,U1,V1,SC,SD见引理2.2.

(2)矩阵方程C Z=D的解矩阵中最小秩和最大秩为:

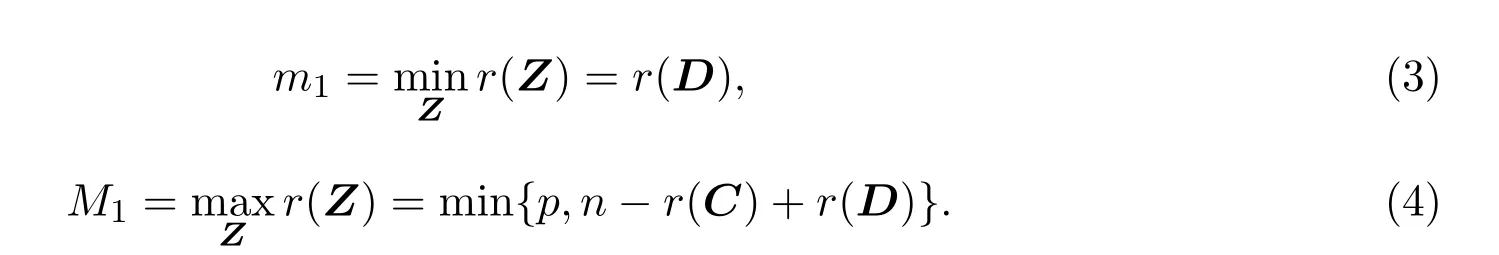
(3)矩阵方程CZ=D的解矩阵中的最小秩解为:

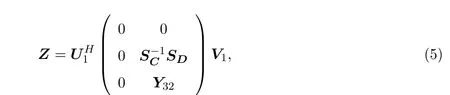
其中Y32是具有相应维数的任意矩阵,U1,V1,SC,SD见引理2.2.

(4)矩阵方程CZ=D的解矩阵中的最大秩解为:

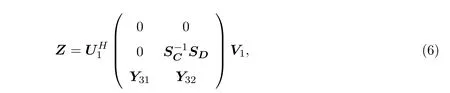
其中Y32是具有相应维数的任意矩阵,选取Y31要么行满秩,要么列满秩.U1,V1,SC,SD见引理2.2.

(5)对于m1≤s1≤M1,矩阵方程CZ=D的解矩阵中具有秩s1的解为:

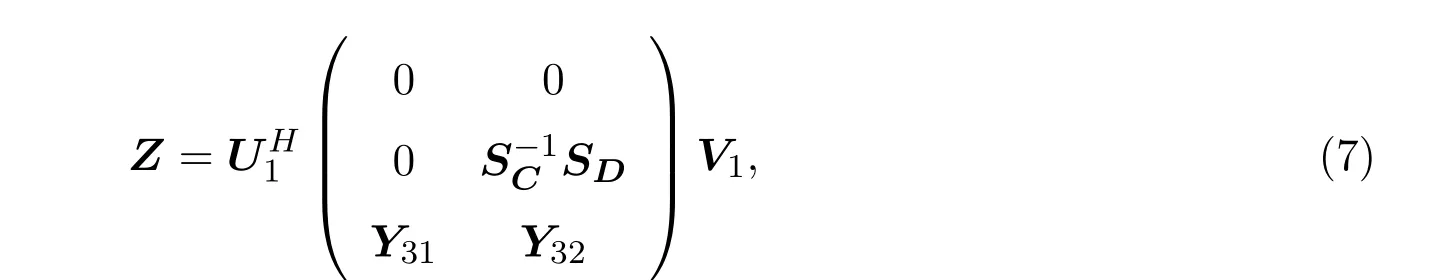
其中Y32是具有相应维数的任意矩阵,选取Y31使得r(Y31)=s1−r(D).U1,V1,SC,SD见引理2.2.

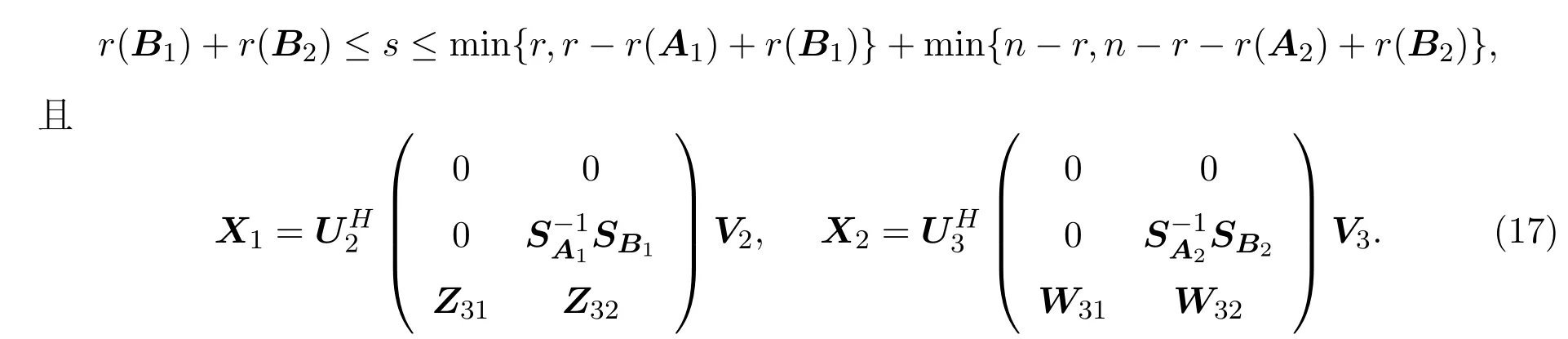
把(17)式代入(16)式,则得到相容矩阵方程AX=B有秩为s的自反解的一般表达式为(14)式.且矩阵方程AX=B的自反矩阵解集合中的最小秩和最大秩为(13)式,以及最小秩解的表达式为(15)式.

3 问题 II解的表达式

参考文献

[1]胡锡炎,张磊,谢冬秀.双对称矩阵逆特征值问题解存在的条件[J].计算数学,1988,10(4):409-418.

[2]肖庆丰,张忠志,顾广泽.广义次对称矩阵反问题的最小二乘解[J].纯粹数学与应用数学,2006,22(4):560-564.

[3]胡锡炎,张磊,周富照.对称正交对称矩阵逆特征值问题[J].计算数学,2003,25(1):13-22.

[4]Chen H C.Generalized reflexive m atrices:special properties and app lications[J].SIAM J.M atrix Anal. App l.,1998,19:140-153.

[5]Cheney E W.Introduction to Approxim ation Theory[M].New York:M cG raw-Hill,1966.

[6]Peng Z Y,Hu X Y.The reflexive and anti-reflexive solutions of the m atrix equation AX=B[J].Linear A lgebra App l.,2003,375:147-155.

[7]M itra S K.Fixed rank solutions of linear m atrix equations[J].Sankhya Ser.A,1972,35:387-392.

[8]Uh lig F.On thematrix equation AX=B with app lications to the generators of controllability matrix[J]. Linear A lgebra App l.,1987,85:203-209.

[9]Xiao Q F,Hu X Y,Zhang L.The symmetric m inimal rank solution of thematrix equation AX=B and the optim al approxim ation[J].Electronic Journal of Linear A lgebra.2009,18:264-273.

[10]G ross J.Nonnegtive-definite and positive-definite solution to them atrix equation AX A∗=B-revisited[J]. Linear A lgebra App l.,2000,321:123-129.

[11]Tian Y G.Ranks of solutions of the m atrix equation A X B=C[J].Linear and M u ltilinear A lgebra., 2003,51:111-125.

[12]Zhang X,Cheng M.The rank-constrained Herm itian nonnegtive-definite and positive-definite solutions to thematrix equation AX A∗=B[J].Linear A lgebra App l.,2003,370:163-174.

[13]Paige C C,Saunders M A.Towards a generalized singular value decom position[J].SIAM J.Numer.Anal., 1981,18:398-405.

The reflex ive m inim al rank solu tion of the m atrix equation AX=B and the op tim al app rox im ation

Xiao Qingfeng1,Hu Xiyan2,Zhang Lei2

(1.Departm ent of Basic,Dongguan Polytechnic,Dongguan 523808,China;
2.College of M athem atics and Econom etrics,Hunan University,Changsha 410082,China)

By app lying thegeneralized singu lar value decom position ofmatrix pairs,thenecessary and suffi cient conditions are obtained for the existence of the refl exive solutions of the m atrix equation AX=B,and the expression of the fixed and m inim al rank solutions is also shown.In addition,for them inim al rank solution set, the expression of the op timal approximation solution to a given matrix is derived.

m atrix equation,reflexivem atrix,generalized singu lar value decom position,m inim al rank, op tim al approxim ation

O241.6

A

1008-5513(2012)06-0719-09

2011-08-26.

国家自然科学基金(10571047);高校博士学科点专项科研基金(20060532014).

肖庆丰(1977-),博士,副教授,研究方向：数值代数.

2010 M SC:65F15,65D 99