城市轨道交通车辆受电弓弓头安全宽度的计算

李向聪 冯大建 凌坤坤

（同济大学铁道与城市轨道交通研究院，201804，上海∥第一作，硕士研究生）

受电弓是城市轨道交通车辆的重要组成部分，但目前国内的受电弓宽度还没有一个统一的标准。受电弓弓头宽度过长则会造成限界加大，从而降低经济性；弓头过短，则会导致脱弓的发生，降低安全性。本文将对能否用更加准确的方法来确定一个安全合理的弓头宽度值进行计算分析。

1 受电弓与拉出值

受电弓主要由10大部分组成（见图1）。其中，底架固定在车体上方，滑板与接触线接触。为了增强弓头滑板的耐磨性，接触线不与轨道线路中心重合。在直线段，采用之字形布置；在曲线段，采用折线形布置。

接触网主要由悬挂支柱、接触线和吊索组成（见图2）。图中A、E点为悬挂定位点，B、C和D点为非悬挂定位点，因此在此处存在受风偏移现象。拉出值是指接触线定位点（A和E点）与受电弓在水平面垂直投影之间的水平距离（直线段称之字值，曲线段称为拉出值）。伸出值是指非悬挂定位点（B、C和D点）与受电弓之间的距离。

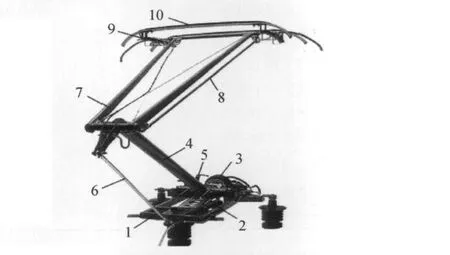
图1 受电弓结构

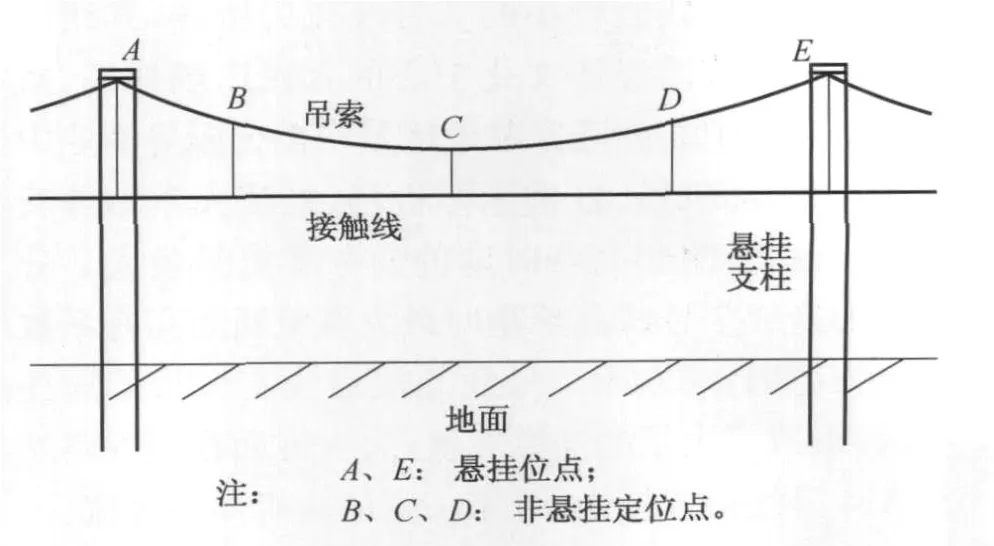
图2 接触网结构

弓网关系除了受拉出值或之字值、伸出值以及大风的影响外，还受曲线超高状态、车体侧滚和横移等因素的作用（见图3）。

如图3中所示，左图为车辆在直线段上的运行状态，右图为车辆在曲线段上的运行状态。车辆在运行中，受电弓偏移主要受车体偏移和弓头相对车体偏移的影响；接触线偏移计算要分在非悬挂定位点处有受风偏移存在和在悬挂定位点处有拉出值或之字值存在两种情况。如图4中所示，（a）和（b）为直线段中的两种情况；（c）和（d）为曲线段中的两种情况。

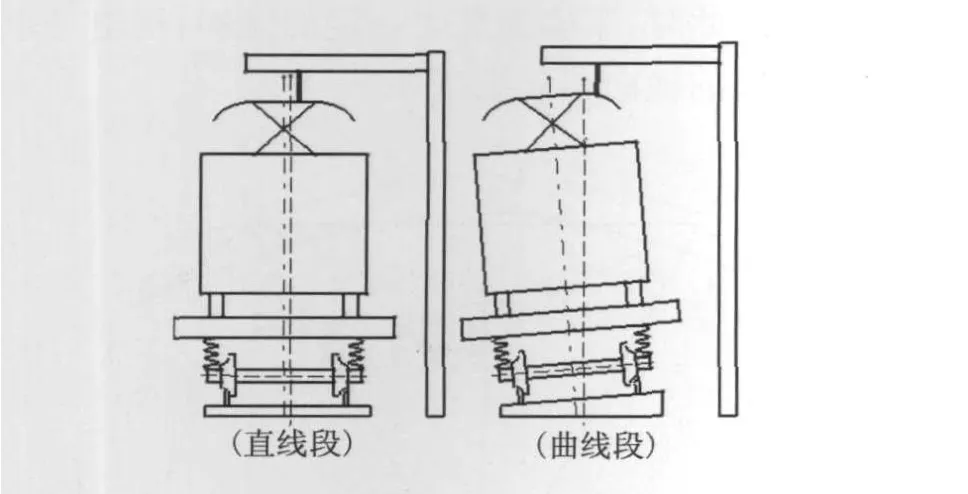
图3 车辆运行状态截面图

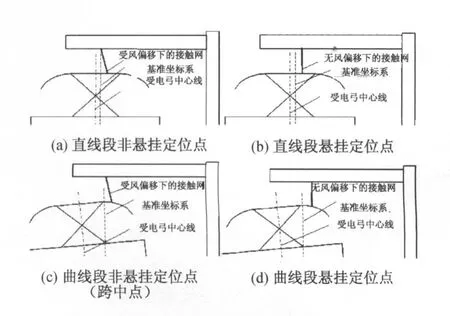
图4 车辆运行局部放大图

2 直线段弓头安全宽度影响因素

直线段受电弓弓头安全宽度主要影响因素分受电弓和接触线两方面。受电弓主要受车体横移和受电弓相对车体横移影响，其中车体横移包括车体横摆和侧滚。接触线主要受拉出值和受风偏移的影响（见图5）。

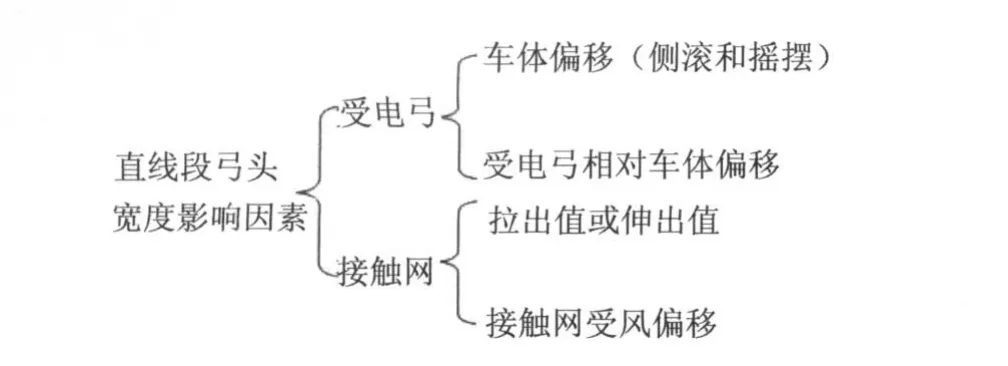
图5 直线段弓头安全宽度影响因素

2.1 直线段受电弓横移（车体横移和受电弓相对车体横移）

直线段的弓头横移主要包括车体横移和受电弓相对车体横移，前者包括车体横摆振动和车体侧滚。当二者方向相同时，车体横移量有最大值。由于车辆、轨道、大风干扰等造成弓头横移的主要计算要素如下：

1）车辆的制造误差值；

2）车辆的维修限度；

3）转向架轮对处于轨道上的最不利运行位置；

4）转向架构架相对于轮对的横向及竖向位移量；

5）车体相对于转向架构架的横向及竖向位移量；

6）车体相对轨道线路的最不利倾斜位置；

7）车辆的空重车挠度差及竖向位移量；

8）因车辆制造载荷不对称等引起的偏斜；

9）车辆一系悬挂及二系悬挂侧滚位移量；

10）轨道线路的垂向及横向几何偏差磨耗维修限度及弹性变形量；

11）曲线段过超高或欠超高引起的车体横移；

12）风力造成的对弓、网接触位置的影响；

13）受电弓相对于车体的横向移动是指在轨面坐标系中，受风力或离心力的作用，受电弓会相对车体产生横向移动。

参考限界标准中的计算公式可以得出，车体的水平横移距离

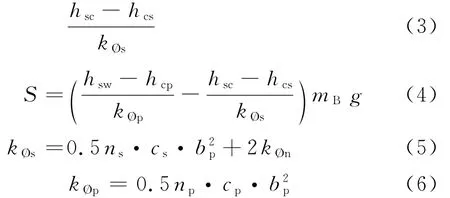
本文中所有公式中符号的意义及单位见文后附录。

2.2 直线段接触线横移（之字值和受风偏移）

直线段的轨道中心线和受电弓中心线行迹是重合的。图6中点1和点3是受电弓悬挂定位点，不存在接触线受风偏移现象。此时受电弓中心线距离接触线的距离为之字值Z。点4为非悬挂点，存在接触线受风偏移量。

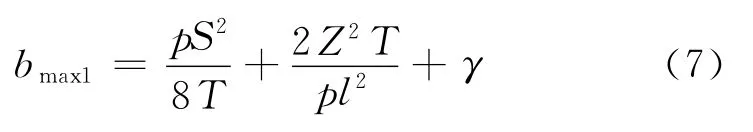
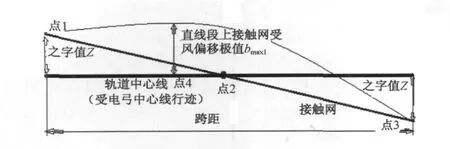
图6 直线段弓网关系图

在点1、3、4处，受电弓均可能会出现脱弓。因此，为了确定弓头安全宽度，需要找出Z与bmax1中的最大值，即：（Z，bmax1）max。

综上所述：在直线段中，受电弓的合理宽度为：

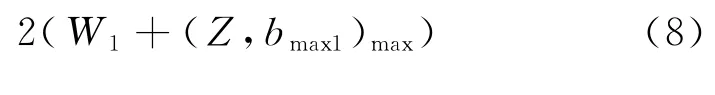
3 曲线段弓头安全宽度影响因素

曲线段受电弓弓头安全宽度求解方法与直线段相似，但需在其基础上考虑曲线超高的影响（见图7）。

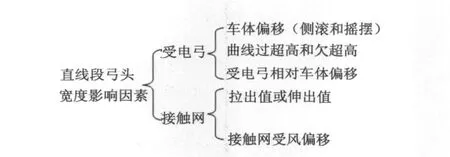
图7 曲线段弓头安全宽度影响因素

3.1 曲线段受电弓横移

3.1.1 车体横移和受电弓相对车体横移

计算方法与直线段相似。参考公式（1），求出由车体横移引起的弓头横移距离为W′1＝W1。

3.1.2 曲线过高超高引起的受电弓横移

轨道车辆在曲线段转弯时，为了平衡离心力，外轨的高度要高于内轨轨道的高度，叫做超高。当实际运行速度不等于设计运行速度时，会造成过超高或欠超高。此时，车体会发生一定的倾斜，受电弓也会发生相应的横向移动见图8。

图8 曲线段弓网关系图

由文献[2]得知，当车辆以小于设定速度通过曲线时，受电弓在跨中E点较容易脱弓。此时列车处于过超高状态，产生的受电弓横向位移

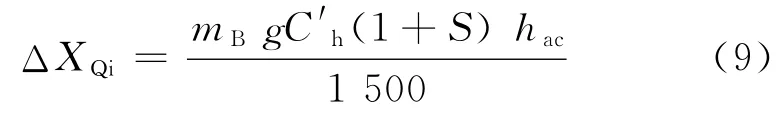
当列车以大于设定速度通过曲线时，受电弓在接触线悬挂定位点M和N点较容易脱弓。此时列车处于欠超高状态，产生的受电弓横向位移

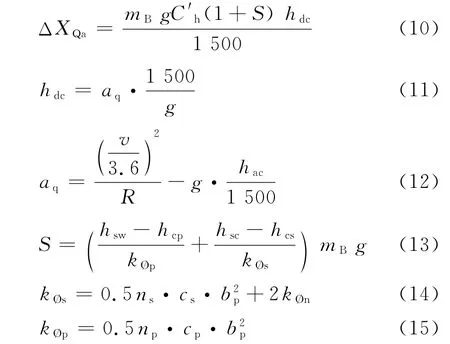
在点M、N、D 处，受电弓均会出现脱弓可能性。在悬挂定位点M、N处，存在定位点拉出值Z，欠超高现象；在跨中D点处，存在伸出值DE，接触线受风偏移量bmax2，过超高现象。因此，为了确定弓头安全宽度，需要在悬挂定位点和跨中两点中找出最终实际的伸出值（即：考虑一切因素下，受电弓中心到接触线的距离）。

3.2 曲线段接触线横移（拉出值和受风偏移）

曲线段的轨道中心线和受电弓中心线行迹是不重合的。如图8所示：点X和点Y是受电弓悬挂定位点，不存在接触线受风偏移。此时受电弓中心线距离接触线的距离为定位点拉出值Z。点E为非悬挂点，存在接触线受风偏移量

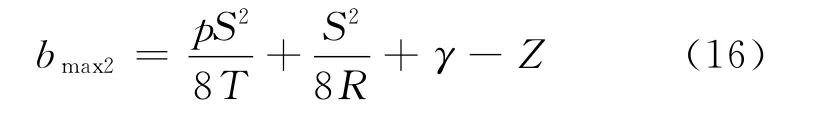
由于W′1是相对轨面坐标系，而受风偏移和超高是相对地面坐标系，所以，二者之间需要进行坐标系转换。

综上所述，曲线段弓网最大横向距离即受电弓最小安全宽度为：

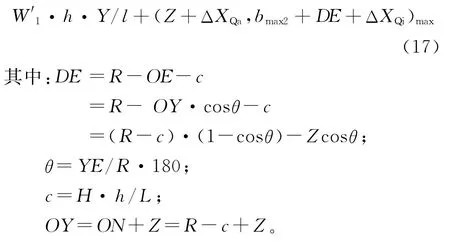
对直线段的合理安全弓头宽度式（8）和曲线段的合理弓头宽度式（17）进行比较，得出最小的弓头安全宽度为：在式（18）的基础上，考虑一定的安全余量和误差计算，可得出合理的弓头长度安全。

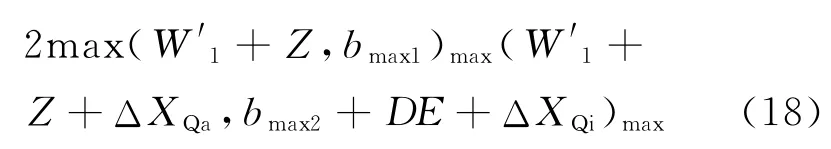
4 城市轨道交通车辆受电弓宽度参数计算软件

利用MATLAB／GUI模块将以上受电弓弓头宽度计算公式编制成软件界面，以方便计算不同参数车辆的弓头宽度（见图9）。

软件分为6个步骤：

1）读取excel格式的车辆参数和接触线参数；

2）计算直线段悬挂定位点处受电弓弓头安全宽度；

3）计算直线段非悬挂定位处受电弓弓头安全宽度；

4）计算曲线段悬挂定位点处受电弓弓头安全宽度；

5）计算曲线段非悬挂定位点受电弓弓头安全宽度；

6）比较直线段和曲线段的弓头宽度结果，得出弓头最终的合理安全宽度。

图9 受电弓弓头宽度计算软件界面图

5 受电弓宽度计算验证

综合文献[3]提供的某A型车的车辆参数和文献[6]某线路的接触线参数，设定拉出值A＝350 mm。将附件中的结构参数输入软件中计算得出该A型车的受电弓最小安全宽度为1187mm。假如设定受电弓弓头宽度的安全余量和误差值为2%，得出弓头的合理安全宽度为1 200mm。

附录：各种符号代表意义以及单位

[1]罗湘萍.全动态包络线地铁车辆限界研究[J].铁道车辆，1997（9）：41.

[2]郭风平，陈唐龙，牛大鹏，等.曲线区段接触线拉出值的确定[J].铁道技术监督，2006（10）：23.

[3]陶功安.地铁车辆限界计算[J].电力机车与电传动，2006（3）：11.

[4]陈中杰.地铁限界问题探讨[J].电力机车与城市轨道交通车辆，2007（6）：50.

[5]于万聚.高速电气化铁路接触网[M].成都：西南交通大学出版社，2003.

[6]叶志荣，徐金平，黄江伟.关于曲线上导线拉出值设定的建议[J].铁道机车车辆，2003（6）：66.

[7]董绍德.接触网[M].北京：中国铁道出版社，2010.

[8]CJJ 96—2003地铁限界标准[S].