基于认知诊断的高考考生能力掌握模式研究

李金波 朱玉玲

1 前言

目前，我国高考还只是报告一个分数（或等级）来笼统地反映考生的知识（能力）水平。至于考生究竟掌握了哪些知识（能力），未掌握哪些知识（能力），还无法做出进一步的分析与解释。对具有相同得分考生之间的知识（能力）差异更是无从得知。随着我国新一轮课程改革尤其是课程评价改革的推进，改变传统的高考评价模式，探索有效的知识（能力）考查和知识（能力）考查程度评估的方法，已为当前之急需。

近年来，心理与教育测量理论逐渐与认知心理学结合，形成了以认知诊断为核心的新一代测评理论。认知诊断理论使学生的知识（能力）诊断成为可能，国内外学者也进行了不少的研究。例如，Tatsuoka（1983）最早提出的规则空间模型就是基于对中小学数学加减法的分析；通过对172个被试在40道带正负号的加减法题目上的作答反应的分析，发现了30种错误规则。Dogan，Tatsuoka（2008）运用规则空间模型分析土耳其学生在TIMSS-R数学测试中的成绩，并将结果与美国同类学生比较，发现土耳其学生在代数和概率统计学、代数中的规则运用、解答开放性问题等方面比美国学生弱。Lee，Sawaki（2009）运用一般诊断模型、融合模型和潜在分类模型三种认知诊断模型对英语作为第二语言的学生听力和阅读理解能力进行评估诊断研究。Chen（2011）对台湾城乡学生间数学成绩进行认知诊断，发现城市学校的学生对高层次的数学内容（几何和代数）和抽象思维能力的表现优于农村学校的学生。而且城市学生大多被归类为掌握较多知识属性的模式，农村学生大多被归入掌握较少属性的知识状态。在大陆，余嘉元（1995）运用规则空间模型对初中二年级学生在解不等式中存在的认知错误进行识别，确定了学生解不等式18种典型错误反应模式，并把86%的被试归入这18种典型认知错误反应模式。戴海崎和张青华（2004）应用认知诊断中的规则空间模型对299名被试进行诊断，判断他们在统计学习中的属性掌握模式。刘启亮（2008）运用规则空间模型对初三学生化学化合物有关知识掌握情况进行了诊断，将91.46%被试的实际作答模式判归为21种理想属性反应模式，从而实现了对被试的属性掌握情况的诊断，并根据诊断的结果就如何补救进行了探讨，从班级和个体两个层面在理论上提出了一些补救设计方案。刘芳（2011）运用规则空间模型通过对3～4年级汉语阅读障碍儿童之快速命名及工作记忆缺陷的认知诊断性测验研究，成功地将95%的被试归类到典型掌握模式中，探讨其结构内容和属性掌握模型，为其诊断提供理论和实践依据。

综合来看，认知诊断理论在知识技能诊断中已经得到了一些成功的运用，但这些应用研究大都是基于某一具体的学科知识（能力），集中在属性层级简单的小规模的研究与应用领域，在更具价值和影响力的大规模测验（如高考）中至今还未见令人兴奋的实际应用。基于此，本研究以高考为研究对象，开展高考考生能力掌握模式的认知诊断研究，尝试认知诊断技术在大规模考试中的推广应用。

2 研究方法

2.1 被试

从参加某省2011年高考理科数学考试的全体考生中随机抽取10 000名考生作为考生整体能力掌握模式诊断样本。另外，从全体考生中随机抽取男生和女生各5 000名作为男女生差异研究样本，城市和农村（按户口所在地划分）考生各5 000名作为城乡考生差异研究样本。

2.2 测验工具

以该省2011年高考理科数学试卷作为测验工具，测验共22个项目（试题）。

2.3 研究程序

运用规则空间模型对考生在测验所考查的能力属性上的掌握模式进行诊断。

第一步，确定能力属性及能力层级关系。根据高考考试大纲（说明）要求以及已有的研究，确定高考理科数学所考查的学科能力包括运算求解能力（B1）、数据处理能力（B2）、空间想象能力（B3）、推理论证能力（B4）、抽象概括能力（B5）、应用意识（B6）和创新意识（B7）共7种。组织学科专家组对能力之间的层级关系进行集中分析和讨论，最终确定它们之间的层级关系见图1。

第二步，由学科专家组对项目所考查的学科能力进行集中讨论，确定每个项目所考查的主要能力结构（见表1）。

图1 能力属性的层级关系

表1 项目能力属性表

第三步，确定邻接矩阵、可达矩阵、事件矩阵、缩减事件矩阵和典型属性矩阵。根据表1和图1标定的7个属性之间的层级关系，可以得到各能力属性的邻接矩阵和可达矩阵。根据所考查的能力属性数量和排列组合原理，可得知考查7种能力属性的所有可能的项目类型（事件矩阵Q）有27-1=127种。考虑7种属性之间存在的层级关系，可以得到7×70的缩减事件矩阵。对缩减事件矩阵进行转置，得到典型能力属性矩阵（见表2，1表示考生掌握了该能力属性，0表示考生没有掌握该能力属性；加上考生属性掌握全为0的情形，共有71种典型的考生能力掌握模式）。

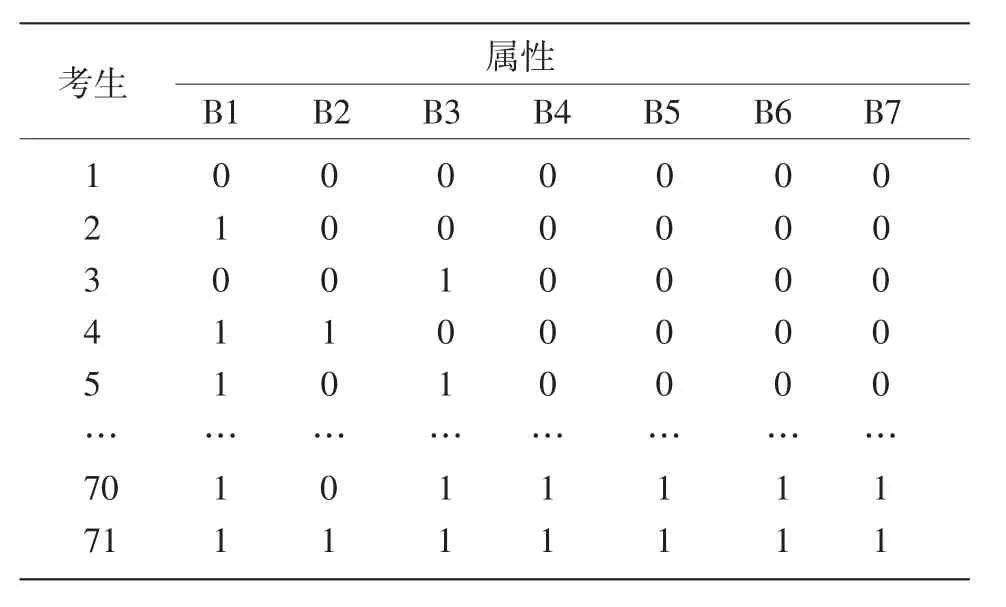
表2 考生典型能力属性矩阵

第四步，确定理想项目反应模式。测验包括客观题（共17题）和主观题（共5题）两部分，可以分别确定其理想项目反应模式。客观题部分，根据考生所有可能的典型属性掌握模式和项目属性可得到与其相对应的在没有失误情况下的71种理想项目反应模式。主观题部分为多级评分。根据罗欢,丁树良（2009）关于属性不等权重时的属性分数权重的计算方法，同样可以确定多级评分的期望项目反应模式。将两部分理想反应模式进行合并，最后可得测验完整的理想项目反应模式矩阵（见表3，第1～17列为客观题反应模式，第18～22列为主观题反应模式）。

表3 理想项目反应模式

第五步，规则空间构建和模式识别。关于认知诊断的模式识别方法，传统多通过计算马氏距离，根据马氏距离的大小将考生的掌握模式进行归类。近年来国内外在此基础上也开发了其他一些分类方法。例如，Gierl和Cui等人（2007）应用多层感知器神经网络进行认知诊断分类，即将期望项目反应模式和对应的典型属性掌握模式分别作为输入项和输出项，建立神经网络模型，再利用模型对实际反应模式进行分类识别。在国内，曹慧媛，丁树良（2009）则使用其他人工神经网络（BP网络、Hamming网络以及PNN网络）进行认知诊断分类，通过对0-1评分的AHM模式分类仿真实验表明，与AHM中以往的模式分类方法相比，人工神经网络方法不仅具有较高的归准率而且更具有自适应性和鲁棒性。基于此，本研究运用MATLAB软件自编程序，建立BP神经网络模型，对高考考生的能力掌握模式进行识别。

首先，输入/输出项设计。由于共考查7种能力，因而输出项神经元个数设置为7个。输入项为理想项目反应模式，包括22个反应项目，因而输入项神经元个数设定为22个。

其次，网络结构设计。网络采用单隐含层结构。根据实际训练结果确定隐含层神经元个数为47个。隐含层的传递函数采用S型的正切函数（tansig）；输出层传递函数采用S型的对数函数（logsig）；学习函数为Learngdm；学习速率为0.1；期望收敛精度选择1×10-8；训练函数选择trainlm算法。

第三，网络训练与仿真。本研究共获得有效测试样本为71个，将其作为训练样本。设计的网络经过34次训练后，其性能就达到了要求。

基于训练好的神经网络，就可以对考生的能力属性掌握模式进行识别。

3 研究结果

3.1 考生整体的能力掌握模式诊断

基于已训练的BP神经网络模型对样本考生的典型能力属性掌握模式进行识别，结果见表4（只取考生比例较大的部分典型能力掌握模式）。

表4 高考考生的能力属性掌握模式

表4显示，在所有的10 000个考生样本中，成功将考生进行能力属性归类的有9 651个，比率为96.51%。这个比例大于一般认为的90%成功分类比例的标准，意味着神经网络技术在能力模式识别得到了成功的运用。

从表4可以看出，考生的能力属性模式比例较高的有第11、33、51、56、66种等属性模式。这几种模式对应的属性模式分别为（1101000）、（1101001）、（1111001）、（1101101）、（1111101）。也就是说，属于第11种典型能力模式的考生掌握了运算求解能力、数据处理能力和推理论证能力，但抽象概括能力、应用意识和创新意识掌握欠缺。其他模式可以依此类推。

如果按考生在各项能力属性的掌握情况进行统计，可以得出如表5所示的各个属性的平均掌握情况。

表5显示，考生在7项能力属性上的掌握比例从96.58%到30.77%不等。

3.2 不同考生群体的能力掌握模式比较

3.2.1 城乡考生能力掌握模式的差异

对城市和农村考生样本分别进行能力掌握模式诊断，结果见表6。

表6显示，城市、农村考生成功归类的比例比较接近，分别为97.32%和96.72%，均达到较高的水平。再对比各种典型能力属性的考生数和比例，无论是城市考生还是农村考生，考生的能力属性模式比例较高的均为第11、33、51、56、66、71种等属性模式。但城市考生与农村考生在具体能力属性上的人数和比例还是存在一定的差异。

分别对城乡考生在各项能力属性上的平均掌握情况进行统计，结果见表7。

表7显示，无论是城镇考生还是农村考生，掌握比例较高的有运算求解能力、数据处理能力和推理论证能力，但应用意识的掌握比例最低。在7种能力中，城市考生在所有能力上的掌握比例均高于农村考生。

表5 考生在各项能力属性的平均掌握情况

表6 城乡考生的能力掌握模式比较

3.2.2 男女考生能力掌握模式的差异

对男女生样本分别进行能力掌握模式诊断，结果见表8。

表8显示，男女考生成功归类的比例比较接近，分别为96.64%和96.24%，均达到较高的水平。再对比各种典型能力属性的考生数和比例，无论是男生还是女生，考生的能力掌握属性模式比例较高的也均为第11、33、51、56、66种等属性模式。但男生与女生在具体能力属性模式上还是存在一定的差异。

分别对男女考生在各项能力属性上的平均掌握情况进行统计，结果见表9。

表9显示，无论是男生还是女生，掌握比例较高的还是运算求解能力、数据处理能力和推理论证能力，但应用意识的掌握比例最低。在7种能力中，男生在所有能力上的掌握比例均高于女生。

表7 城乡考生在各项能力属性上的平均掌握情况

表8 男女考生的能力掌握模式比较

表9 男女考生在各项能力属性上的平均掌握情况

4 分析与讨论

综合上述分析结果，可以发现以下一些特征：

首先，考生对各项能力属性的掌握程度差异明显。考生的典型能力掌握模式共有71种，96%以上的考生可以归属于相应的典型能力掌握模式，并且不同典型能力掌握模式的人数比例从0到9.8%不等（见表4）。其中，比例最高的是第33种典型能力掌握模式，达到9.81%。该部分考生对运算求解能力、数据处理能力和推理论证能力掌握比较好，也具有较好的创新意识，但在空间想象能力、抽象概括能力和应用意识方面比较弱。第71种典型能力掌握模式的考生比例为6.37%，即全面掌握各项能力的考生人数占6%以上。从整体来看，考生掌握程度较高的有运算求解能力、数据处理能力和推理论证能力（均在90%以上），掌握程度较低的有应用意识、空间想象能力和抽象概括能力，尤其是应用意识的掌握比例最低（不到31%）。

其次，不同考生群体的能力掌握模式存在不同程度的差异。选取城乡和男女两个不同考生群体进行能力掌握模式差异的分析。发现城乡考生在不同典型能力掌握模式上的考生数和比例存在差异。总体而言，在低端能力掌握模式上农村考生的比例要高于城市考生，而在高端能力掌握模式上则相反。在第71种典型模式上，城市考生的比例要高于农村考生，即全面掌握各项能力的考生人数城市多于农村。在各项能力的平均掌握比例上也是城市考生高于农村考生。

男生与女生在具体能力掌握模式上也存在一定的差异。例如，在全面掌握各项能力（第71种典型模式）的比例上，男生要高于女生（分别为7.28%和4.90%）。从各项能力的平均掌握比例来看，也是男生均要高于女生。其中，差异尤为明显的有空间想象能力和抽象概括能力。

5 结论

（1）基于神经网络建模技术可以对高考考生的能力掌握模式进行有效的识别，可以进行推广应用。

（2）根据2011年某省高考测试卷对考生能力掌握模式进行分析，显示考生之间的能力掌握模式不同，不同的典型能力掌握模式的考生比例也不同。考生对运算求解能力、数据处理能力和推理论证能力的掌握程度较高，对应用意识、空间想象能力和抽象概括能力的掌握程度较低，尤其以应用意识的掌握程度最低。

（3）不同考生群体的能力掌握模式存在明显差异。城市考生在各项具体能力上的平均掌握率高于农村考生；在高端能力掌握模式上的比例高于农村考生，在低端能力掌握模式则相反。男考生对各项能力的平均掌握率要高于女考生，差异较为明显的有空间想象能力和抽象概括能力。

（4）研究结果将考生的能力掌握模式划归到71种典型的能力掌握模式中，考生可以根据自己的能力掌握模式了解自己能力的具体掌握情况，教师可以根据能力掌握情况进行有针对性的补救教学，从而提高教学以及学习效率。

[1] 曹慧媛，丁树良.人工神经网络在认知诊断中的应用研究[D].南昌：江西师范大学，2009.

[2] 戴海崎,张青华.规则空间模型在描述统计学习模式识别中的应用研究[J].心理科学,2004(04):949-951.

[3] 刘芳.3～4年级汉语阅读障碍认知诊断测验初编:基于RSM的儿童快速命名和工作记忆缺陷的诊断研究[D].长沙：湖南师范大学,2011.

[4] 罗欢,丁树良.认知诊断中属性权重的研究——以多级评分AHM为例[D].南昌：江西师范大学，2009.

[5] 刘启亮.规则空间模型在初中生化学知识学习诊断与补救中的应用研究[D].南昌：江西师范大学，2008.

[6] 余嘉元.运用规则空间模型识别解题中的认知错误[J].心理学报，1995（2）：196-204.

[7] Chen,Y.H.Cognitive Diagnosis of Mathematics Performance between Rural and Urban Students in Taiwan[J].Assessment in Education:Principles,Policy&Practice,2011(10):1-17.

[8] Dogan,E.,&Tatsuoka,K.K..An International Comparison Using a Diagnostic Testing Model:Turkish Students’Profile of Mathematical Skills on TIMSS-R[J].Educational Studies in Mathematics,2008(3):263-272.

[9] Gierl,M.J.,Cui,Y.,&Hunka,S.Using Connectionist Models to Evaluate Examinees’Response Pattern on Test:An Application of the Attribute Hierarchy Method to Assessment Engineering[C].Paper Presented at the Annual Meeting of the National Council On Measurement in Education.Chicago,USA,2007.

[10] Lee,Y.W.,&Sawaki,Y.Application of Three Cognitive Diagnosis Models to ESL Reading and Listening Assessments[J].Language Assessment Quarterly,2009(6):239-263.

[11] Tatsuoka,K.K.Rule space:an approach for dealing with misconceptions based on item response theory[J].Journal of Education Measurement,1983(4):345-354.