彩虹为什么是弯的？

从小就知道彩虹，但你知道彩虹为什么是弯的吗？想必很多人都见过彩虹（至少彩虹的照片你见过吧）。一说到它，你脑海里总能浮现出一道七色圆弧。但你知道彩虹为什么是弯的吗？彩虹真的是恰好七种颜色吗？彩虹的秘密，死理性派告诉你。

古代人对彩虹的观察和研究

对彩虹的研究最早可以追溯至公元前 4 世纪。亚里士多德是第一个认真研究彩虹的人，他曾指出彩虹最为重要的几个特征，比如：

·如果太阳在地平线上升起得不太高，彩虹就会出现。彩虹不会出现在夏日的中午

·我们可以同时看到两条形状相同但颜色顺序排列相反的彩虹，其中外侧那条显得略为松散

·彩虹主要由三种（或四种）颜色组成（现代的RGB三原色理论亦基于此）

但是有一个很重要的现象亚里士多德并没有注意到，那就是两条虹中间的区域亮度较暗，直到公元约 200 年雅典哲学家亚历山大（Alexander of Aphrodisia）才观察到这个现象，所以后人就将这条暗带命名为“亚历山大暗带”（dark band of Alexander）。另外，亚里士多德对彩虹的解释并不正确，他认为只有大的镜子可以反射出物体的全部外形，他把天空中的水滴比做小镜子，认为这个镜子太小了，不可能反射出整个太阳，但是又必须得有什么东西反射出来，所以会有颜色呈现出来。而且，亚里士多德也没有注意到光的折射作用。

在此之后，古罗马哲学家 塞内卡 、波斯物理学家 海什木等人也都曾发表过自己的看法。中国北宋时期一位叫 孙思恭 的精通天文历算的进士也曾说过“虹乃雨中日影也，日照雨则有之”（沈括《梦溪笔谈》），这些均只停留在对现象的思考上，没有更多深入和本质性的研究。

彩虹是怎么形成的

我们现在知道，彩虹的形成和光的折射有关。所以直到人们发现折射定律，彩虹问题才有条件被解决。光入射到不同介质的界面上会发生反射和折射，入射光和折射光位于同一个平面上，且与法线的夹角满足如下关系：

其中 ， n 1 和 n 2 分别是两个介质的折射率 ， θ 1 和 θ 2 分别是入射光（或折射光）与法线的夹角，叫做入射角和折射角。这个定律最早在公元 984 年被波斯科学家 IbnSahl 精确描述。随后又被英国科学家 托马斯·哈利奥特 （ 1602 年）、荷兰物理学家 威理博·斯涅尔 （ 1621 年）、法国数学家笛卡尔（ 1637 年）等人先后独立发现这个定律。

其中，笛卡尔利用折射定律，成功解释了彩虹是如何形成的。笛卡尔假想在一个 AFZ 平面内，光线从 AF 处射出，人眼位于 E处。如果这时把一个代表水滴的圆球放在 BCD 处，那么 D 部分将呈现全红色且比其它部分都更明亮。而无论是把球向前向后还是向左向右移动，这个现象均不会改变。笛卡尔测出此时的∠DEM 约为 42° （ M 为彩虹的圆心）。之后他将 ∠DEM 调得稍大一些，观察到红光立刻就消失了，稍小一些，则能看到黄色、蓝色等其它颜色。在仔细检查 BCD 处的球后，笛卡尔得出结论：光线 AB 在 B 点处射入球体发生折射打到 C 点，随后在 C 点处发生反射传递到 D 点，并在 D 点再次发生折射而出。

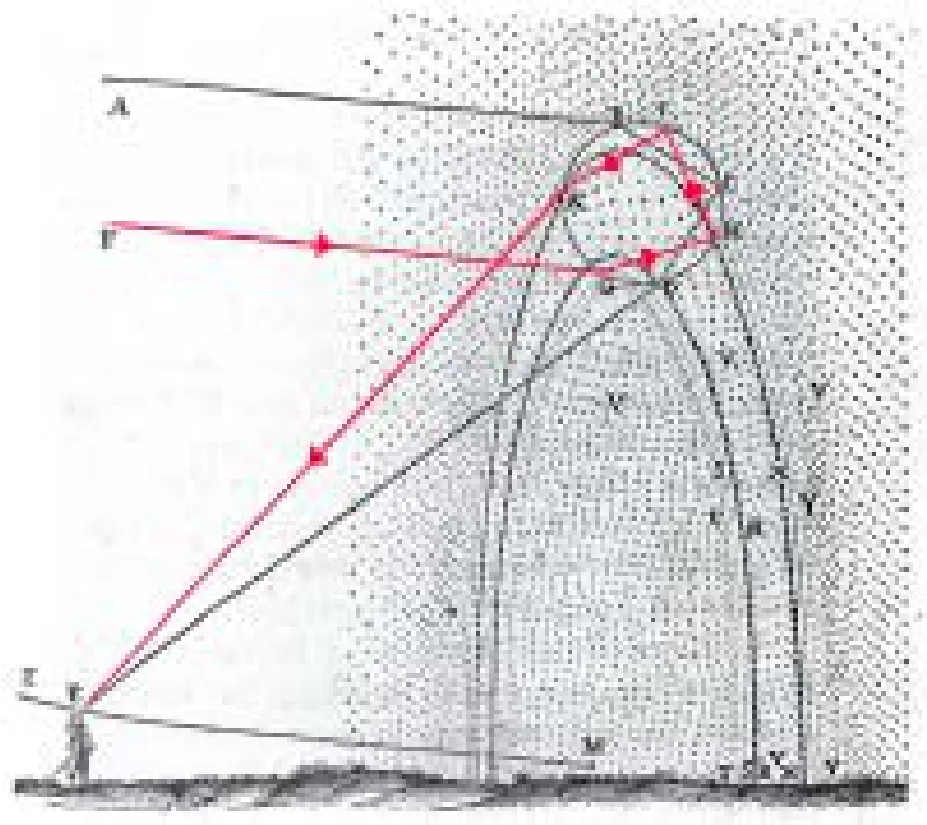
笛卡尔描绘彩虹是如何形成的。

上面这段话并不太好理解，转化成现代语言就是：以空中的一个水珠为例，如下图所示，光线在水滴内发生两次折射和一次反射。其中α为入射角，β为折射角。容易看到，角 D（α）就是最后的光线偏离原始方向的角度。

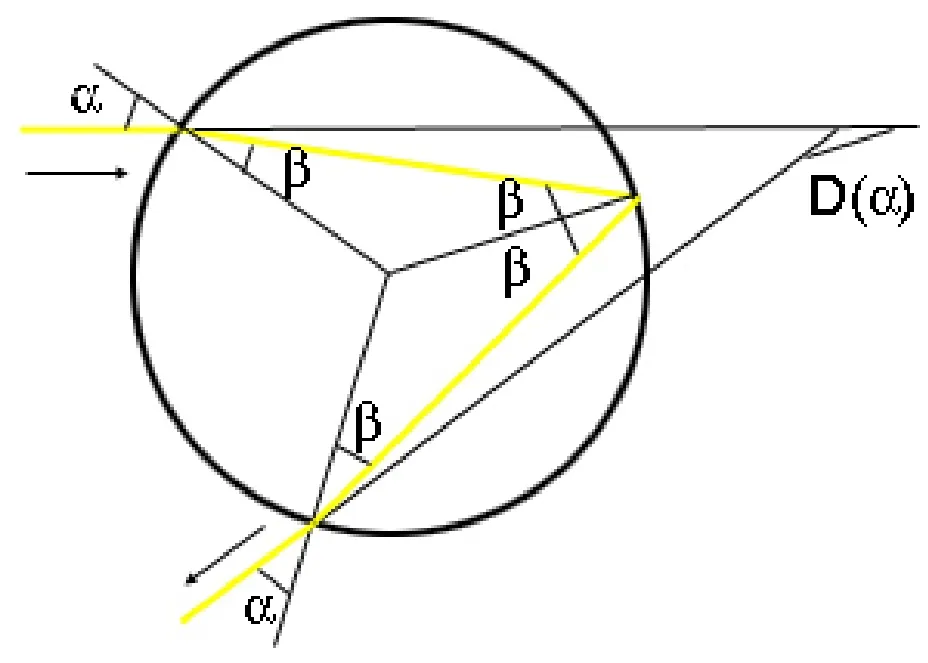
那如果一簇平行光线射入水珠又是什么情况呢？如下图所示，可以发现经水珠两次折射后，一部分光线散射出去，还有一部分光线则非常密集地射向（大致的）同一方向。实际上 可以证明 ，下图中越靠近红线处的光线越密集，光强越大。这条红线就被称作为彩虹线。

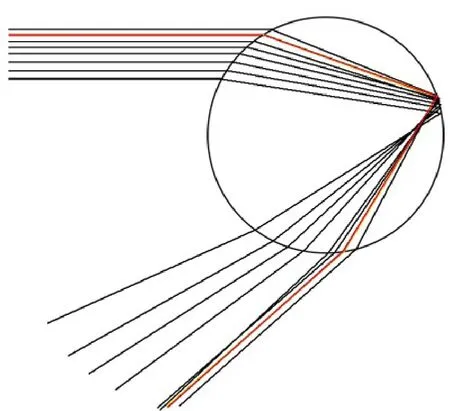
要确定这条彩虹线的位置也并不困难。仍然以红光为例，前面已经说过，角 D（α） 是最后的光线偏离原始方向的角度。通过简单的几何知识我们容易得到：

其中， n f,w 是红光在水中的折射率（1.33），将上式代入到D f （α） 的表达式中，绘制 D f （α） 的函数图象如下图蓝线所示。从函数图中我们可以看到，当入射角 α 范围相等时（ I 1 = I 2 ），最后的光线偏移量范围 J 1 比 J 2 间隔更小，也就是说入射角在 I 1 范围内的入射光线（入射光线是平行的，但由于水珠是球形，所以几乎每条光线的入射角都不相等，而是在一个范围内），光线偏移量的范围更小。即两次折射后的光线更加密集，光强更大。

因此， D f （α） 的最小值就对应着彩虹线的位置。通过求导计算，当 α=59.58° 时有最小值 Df (α) =137.48° 。因此，最终的折射光线和入射光线的夹角是 180°-137.48°=42.52°。这正是笛卡尔寻找的 ∠DEM，也就是人眼对于彩虹的仰角，称为红光的“彩虹角”（Rainbow angle）。我们所看到的彩虹中红色部分均来在这一角度附近。

当以人的眼睛为顶点，把所有与平行入射光线成 42.52° 彩虹角的光束连接起来，就形成一个红色的圆锥体。 圆锥底面的圆弧就是彩虹。到这里，我们就成功解决了彩虹为什么是弯的这个让无数人困惑的难题。

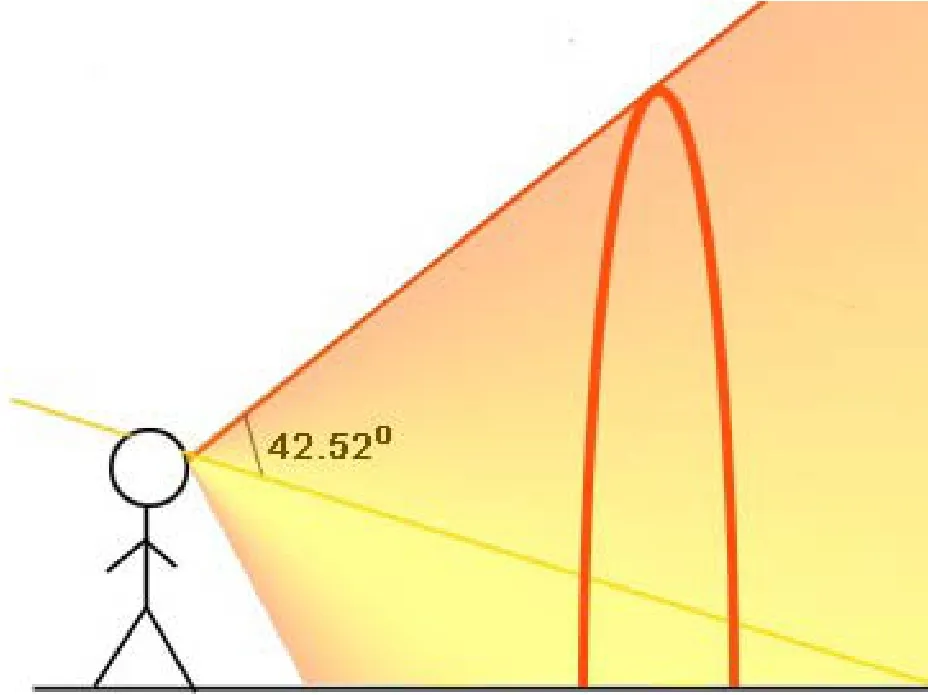
所有满足红光彩虹角形成的红色圆锥体。

另一方面，对红光的分析还可以拓展到其它颜色的光线。这样就可构建出彩虹的完整的彩色外形。比如对紫光分析，由于其频率比红光高，折射率要高于红光，所以能计算出其彩虹角为41.07°（取紫光在水中折射率为1.34）。这个值小于红光，这正是为什么在彩虹中，紫色排在红色下方的原因。

为什么中午很难看到彩虹

顺带一说的是，你在中午几乎看不到彩虹。因为从上面的示意图我们可以看到，太阳位于底面圆心（即彩虹的圆心）与人眼连线的延长线上，这导致了彩虹不会出现在中午——太阳越高，彩虹的圆心将越往地平线以下偏移，这使得彩虹整体下移。当然如果从空中俯瞰的话，可以观察到完整的圆形彩虹。如果没有飞机，站在视野开阔的高山之巅也有可能看到。

彩虹不会出现在中午的原因。

彩虹是七色的吗？

说完彩虹的形状，不妨再说说彩虹的颜色。一种广为流传的说法是彩虹由 7 种颜色组成。但事实上彩虹是一道由红色到紫色的连续光谱（“光谱”一词最先由牛顿创造），并非真的只是由 7 种泾渭分明的颜色组成。1665 年牛顿在棱镜实验中将可见光分为红、橙、黄、绿、蓝、靛、紫这 7 种颜色，实际是受到了来源于古希腊的毕达哥拉斯学派的影响。毕达哥拉斯学派认为数学是美的（比如他们搞出的“黄金分割”），在祷文中他们认为 1 是纯洁的， 4 是圣洁的， 10 是万物之母，而数字 7 则象征着完美。在牛顿之前，“七原色”（seven principal colours）的概念就已出现在中世纪的神秘主义和炼金术理论之中，并在文艺复兴时期成为遵行的颜色理论。

由于不同颜色光的波长都不相同，所以彩虹实际就是可见光的色散，介质就是雨后天空中的水滴。人的眼睛可以感知的电磁波波长一般在 400 到 700 纳米之间，而这只占宽广的电磁波谱的极小部分。

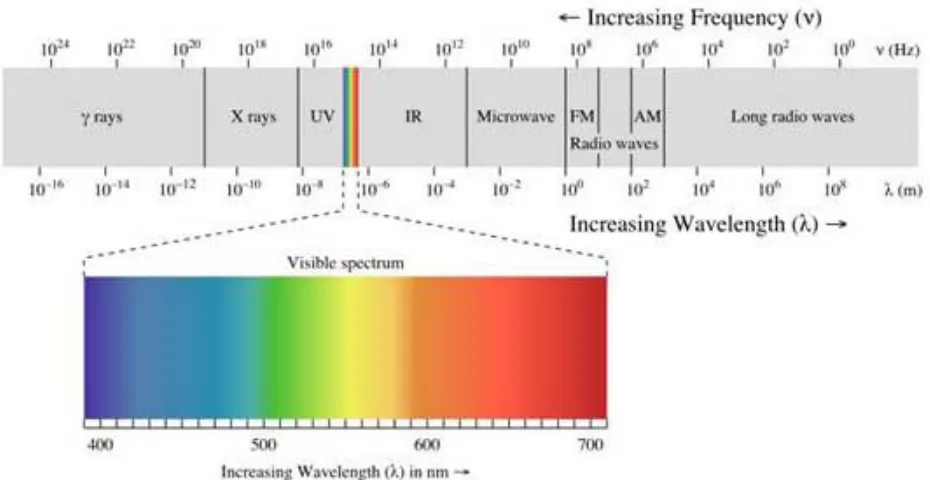
可见光光谱。

多重彩虹和亚历山大暗带

虽然牛顿在对彩虹的研究中颇有发现，但是在对彩虹的进一步阐释中，由于牛顿深陷于光的粒子性理论之中，因此无法解释“复虹”（supernumerary rainbow，指有时在一条彩虹的内部还可以看到几条模糊的彩虹）的存在。

直到 1801 年，英国科学家托马斯 杨意识到了光在一定条件下还具有波的性质，并用双缝实验给予了有力的证明。随后（1804 年）他用“光的干涉”理论完美解释了复虹现象：当两条光束从同一个水滴沿相同方向散播出来的时候，它们彼此之间会发生干涉。若两光束的光程相差半波长的奇数倍，则到达观察者的光强彼此削弱；若相差整数波长，则光强相互增强。由此造成了一系列位于彩虹内侧的明暗相同的光带。根据这一解释，“复虹”又被称为“干涉虹”。

在上文中我们分析的彩虹又可称为“主虹”（primary rainbow）。在主虹上方，我们有时还能看到“副虹”（secondary rainbow），也就是文章开头提到的亚里士多德观察到的两条形状相同但颜色顺序排列相反的彩虹的外一层，即我们常说的“霓”。虹是光在水滴内经过了两次折射和一次反射的结果，霓的形成则比虹在水滴内多经历了一次反射（就是笛卡尔描述彩虹怎样形成示意图中的红色光线所示），导致它的颜色排布与虹的颜色排布顺序相反。霓中不同颜色的光线的彩虹角约在 51°左右，所以它比虹显得要高。在自然界中，我们最多能观察到一条副虹，而更高阶的副虹则可以通过实验手段制得。

到这里，霓虹之间的“亚历山大暗带”也可以得到解释了：人眼所能捕捉的光线几乎全部集中在彩虹线及以下处，而几乎没有或者很少有光线高于彩虹线射出，所以虹的上半部是是偏暗的。彩虹线以下射出的光束基本上都是混合了光谱的颜色，呈可见光白色，所以虹的内部要更明亮。霓的分析与之相对，由此形成“亚历山大黑带”（也就是仰角大约在 42°到 51°之间）。

关于彩虹各种观察现象的科学讨论还有很多很多，曾经还有人为之还出了一本书，书名为《彩虹桥：艺术、神话和科学中的彩虹》（The rainbow bridge∶ rainbows in art, myth, and science by Raymond L.Lee,Alistair B.Fraser）。本文只讨论了彩虹现象其中极小的一部分，涉及到了几何光学、波动光学等知识。20 世纪的时候，还曾有科学家用电磁波理论、光子理论等对彩虹现象进行更精确的描述。