实序列FFT算法的存储单元图解析方法

赵鸿图，陈书平，吴尧辉

（1.河南理工大学计算机科学与技术学院，河南焦作 454003；2.焦作煤业集团公司职工教育培训中心，河南焦作 454002；3.河南理工大学电气工程与自动化学院，河南焦作 454003）

0 引言

库利（J.W.Cooley）和图基（J.W.Tukey）基于离散傅里叶变换（discrete fourier transform，DFT）的周期性和对称性所提出的快速傅里叶变换（fast fourier transform，FFT），极大地减少了离散傅立叶变换的计算复杂度，使其广泛应用在信号处理、通信工程、控制系统等各个领域，而且其在现代数字信息时代的作用和地址越来越突出。智能芯片的快速发展给快速傅里叶变换（fast fourier transform，FFT）的应用提供了硬软件基础。利用智能芯片提供的汇编语言系统编写FFT 汇编语言程序，一方面能充分规划与利用智能芯片的有限资源，另一方面也能够提高程序运行效率。但是，汇编语言程序的编写与理解都非常困难，有必要寻求一种有效的方式在汇编语言层面对FFT 算法进行解析。

现有文献［1－5］对FFT 算法的解析只进行到高级语言层面。虽然文献［6－10］给出了汇编语言程序，但是由于没有给出编程思路与解析图示，使得这些程序都难以阅读和理解，而且如果直接应用这些程序一旦出现错误，使用者不知该如何纠正，即使编程者本人修改起来也颇费心思。为了阐释编写FFT 汇编语言程序的思路方法，结合汇编语言直接作用于硬件的特点，以存储单元图的方式在DSP TMS320C54X硬件资源及其汇编语言系统环境下对实序列FFT 算法进行解析。

1 FFT算法的汇编语言解析思想

为了便于利用汇编语言编程实现FFT 算法，依据汇编语言能够合理规划存储空间且比高级语言运算功能弱的特点，把FFT 算法分解为复序列的FFT、复序列FFT的共轭对称与反对称部分、实序列的FFT 等3个运算功能模块，每个模块分为输入数据、运算方法、输出数据等3项，以数据存储单元图的方式可视化地表现运算过程。

数据存储单元图是内存中存放数据的连续单元区域，它包括输入数据存储单元图、输出数据存储单元图与运算规则3部分。运算规则用存储单元图中数据之间的连接线及其标注描述输入数据产生输出数据的规则以及数据存放位置之间的关系。存储单元图的可视化显示方式为清楚明白地解析算法，进而针对数据存储的位置关系按运算规则进行编程提供了依据。

2 FFT算法原理

2.1 复序列基2DIT－FFT算法公式

假设复序列x（n）的长度为N＝2M（M为正整数），即该序列的2DIT－FFT 算法分解为M 级复数运算，那么由第m－1级（X0就是倒位序后的原始数据）的相关数据计算第m 级、第i个蝶组、第k个蝶形的复数计算公式［11］如下

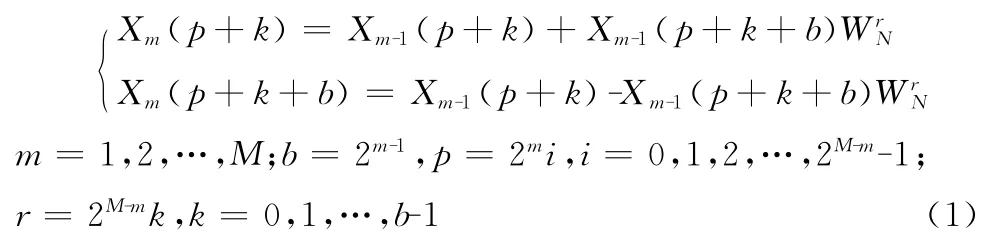
令X（k）＝XR（k）＋jXI（K），代入式（1）得FFT的实、虚部如式（2）所示。式中，b＝2m－1表示每个蝶组的蝶形数、一个蝶形的上下翅间距或本组首个蝶形的下翅与下组首个蝶形的上翅的距离；p＝2mi（i＝0～2M－m－1）是第i个蝶组的地址；r＝2M－mk，k＝0，1，…，2m－1－1是伴随蝶形k的正余弦函数自变量。

此公式说明了FFT 算法包括了级m、蝶组i与蝶形k三层循环。所用到的正、余弦值是在0～π范围内等间隔点位置的值。可以提前计算出0，π／N，…，（N－1）π／N 点的正、余弦值，并依次存放在正、余弦区域的连续N个单元中。那么m 级第i个蝶组的正、余弦值可如此循环取得：首先使指针指向正、余弦区域首地址，取得0角度的正、余弦值；然后使指针增加2M－m＋1（即2△r）得到下一点的正、余弦值，2m－1－1次后就可以取到所有需要的正、余弦值；最后再增加2M－m＋1使指针回到正、余弦区域首地址，取得第i＋1个蝶组的正、余弦值。

2.2 实序列FFT算法

利用N 点复序列的FFT 算法计算2N 点实序列的FFT算法的过程［12］如下

（1）将序列x（n）分为偶奇序列xe（n）和xo（n）；

（2）构造复序列y（n）＝xe（n）＋jxo（n）；

（3）由式（2）计算Y（k）＝YR（k）＋jYI（k）；

（4）求Y（k）的共轭对称与共轭反对称的实、虚部Re、Io与Ro、Ie

3 FFT算法的存储单元图解析法

假设实序列x（n）有2N个，存储在C54X的DARAM的首地址为INPUT 字区间。倒位序后的数据存放在DARAM的首地址为DATA的2N个字区间。将FFT 算法解析为如下3个过程。

3.1 复序列的FFT算法的存储单元图解析

3.1.1 数据位倒序

（1）数据分组。从INPUT 开始，每2个数据为一组，共分为N 组。每组中的两个数据组成一个复数，其中第一个数据为复数的实部，第二个数据为复数的虚部；N 组组成一个长度为N的复序列。

（2）设置初始状态。AR0＝N，AR2指向INPUT，AR3指向DATA，循环缓冲器长度BK＝2N（实部与虚部总长度），块循环寄存器BRC＝N－1。

（3）移动数据。AR2所指向位置的连续两个单元的数据移入AR3所指向的两个连续单元。

（4）改变AR2与AR3所指向的单元。由AR2＋0B 以位倒序方式使AR2指向下一个数据单元，AR3增加2。

（5）利用RPTB循环执行步骤3～4共N 次。

3.1.2 各级蝶形运算

DATA 处的数据按组表示为D（n），其实、虚部分别为DR（n）与DI（n），n＝0，1，2，…，N－1，共N 组数据。块循环寄存器BRC用于存放蝶组数。

（1）第一级蝶形运算

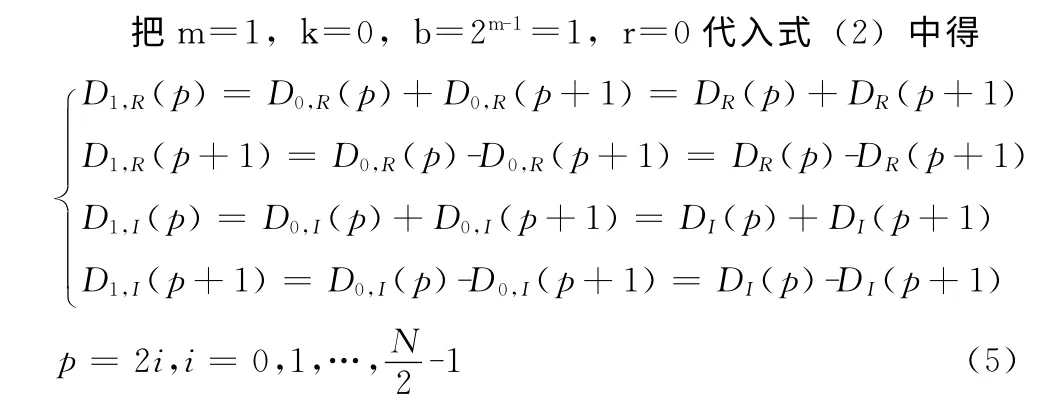
由此，第一级蝶形运算过程的存储单元图解析如图1所示。

图1 基2DIT－FFT的第一级原位运算存储单元

图1中，AR2与AR3分别指向第i＝p／2个蝶形的实部DR（p）与DR（p＋1），AR0＝3为相邻蝶组间距。待计算完每个蝶形的实虚部后，指针AR2与AR3都增加3转入下一个蝶形。BRC＝N／2－1，利用RPTB 指令完成N／2个蝶形的计算。另外，图示时，左侧存储区表示输入数据，右侧存储区表示输出结果，中间是运算过程。实际上，由于采用原位运算，左右侧存储区为同一个存储区，下面各图可作相应理解。

（2）第二级蝶形运算

①k＝0，第一个蝶形

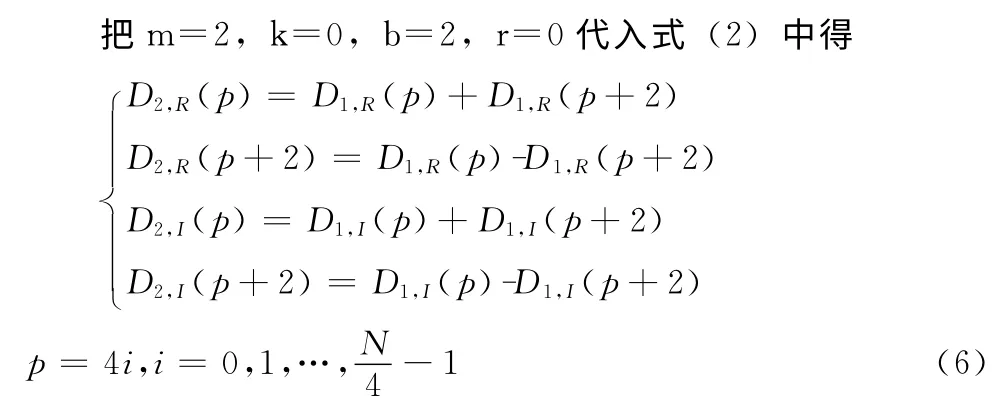
②k＝1，第二个蝶形

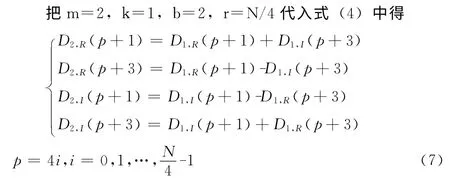
第二级蝶形运算过程的存储单元图解析如图2所示。

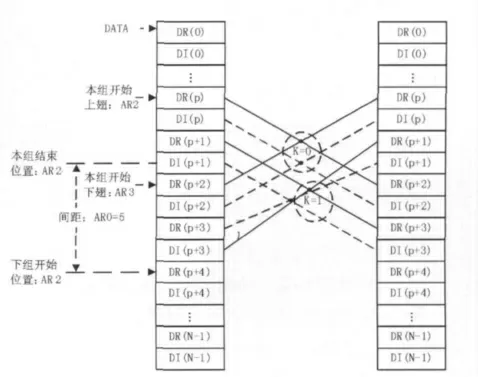
图2 基2DIT－FFT的第二级原位运算存储单元

图2中，AR2指向第i＝p／4个蝶组第一个蝶形的上翅实部DR（p），AR3指向第一个蝶形的下翅实部DR（p＋2），第一个蝶形的运算与第一级相同，如图2中的第一个圈框住的4条线。计算完第一个蝶形，AR2与AR3分别指向DR（p＋1）与DI（p＋3），进入第二个蝶形的计算。如图2中第二个圈框住的4条线。AR0＝5为相邻蝶组的间距。BRC＝N／4－1，利用RPTB指令完成N／4个蝶组的计算。

（3）第三级到最后一级蝶形的运算

1）初始变量的赋值

蝶形两翅间距：由于蝶形的每翅包括实部与虚部，且各占一个单元，所以，蝶形两翅间距是d＿wings＝2×23－1。后续级的蝶形两翅的间距依次对d＿wings加倍即可。

正余弦值：第3级2r的增量为N／23－1，此值存入DARAM的cs＿idx单元中。AR6＝每个蝶组中的蝶形个数－1＝d＿wings－1。AR4、AR5分别指向余弦、正弦区首地址。通过赋值AR0＝cs＿idx、BRC＝AR6，并执行指令AR4＋0%与AR5＋0%依次找到对应的余弦与正弦值并实现BRC＋1次循环。后续级的2r增量依次对cs＿idx减半，AR6通过d＿wings更新。

2）单个蝶形运算的存储单元图解析

把式（2）的单个蝶形运算的存储单元图解析为图3所示。

图3 FFT 第m（≥3）级原位运算存储单元

3）复序列FFT 算法流程图

三层循环流程如图4所示。图中蝶形循环是内循环，由块循环指令RPTB与循环次数控制器BRC 实现；组循环是中循环，由循环指令BANZ与次数控制器AR1实现；级别是外循环，由循环指令BANZ与次数控制器AR7实现。

3.2 复序列FFT的共轭对称与反对称部分算法的存储单元图解析

复序列FFT的共轭对称与共轭反对称部分是复序列转为实序列的桥梁。式（3）的存储单元图解析如图5所示。

图5中，共轭对称与反对称的实、虚部共占用4N个单元，数据存放方式是为了后续计算XR（k）与XI（k）的方便。对于k＝0、N，由式（3）有Re（0）＝Re（N）＝YR（0）、Ie（0）＝Ie（N）＝YI（0）、Ro（0）＝Ro（N）＝Io（0）＝Io（N）＝0。所以，循环从k＝1开始，BRC＝N／2－2，RPTB指令循环N／2－1次。

图4 基2DIT－FFT 三级循环运算流程

3.3 实序列FFT算法的存储单元图解析

3.3.1 k＝0、N 时的FFT

把k＝0、N 代入式（4），得到XR（0）＝Re（0）＋Ie（0）、XR（N）＝Re（0）－Ie（0）、XI（0）＝XI（N）＝0。使AR2指向DATA 即Re（0），AR3指向DATA＋1即Ie（0），AR4指向DATA＋2N 即Io（N）也是XR（N），经过简单计算可以完成k＝0、N的FFT。

3.3.2 k＝1，2，…，N－1时的FFT

图5 共轭对称与反对称的实虚部的存储单元

式（4）的存储单元图解析如图6所示。图中实线表示由Re、Ie生成XR的运算过程，虚线表示由Re、Ie生成XI的运算过程。AR4与AR5分别指向余弦与正弦区域的首地址，指针增量为1。BRC＝N－2，RPTB指令循环N－1次。

图6 由共轭对称与共轭反对称的实部与虚部生成实数FFT的存储单元

4 仿真结果

在前述FFT 算法解析的基础上，编制汇编语言程序，为了防止溢出，每次蝶形运算的结果除以2。假设常数pi＝3.1415926，输入数据是2个正弦信号的叠加，其角频率分别为w1＝2＊pi＊100Hz，w2＝2＊pi＊200Hz，采样频率fs＝512Hz，采样点数2N＝256。输入数据为：input［n］＝（cos（w1＊n／fs）＋cos（w2＊n／fs））／2＊32768，n＝0，1，…，2N－1。

4.1 仿真主要程序

根据上述解析方法，采用DSP TMS320C54X 汇编语言编制实序列的FFT 程序。程序主要由4个子程序组成：

（1）init：初始化子程序，设置初始参数。

（2）datarep：数据位置重新放置子程序，实现初始输入数据按2DIT－FFT 所要求的顺序存放。

（3）fft256：256点由复序列FFT 计算实序列FFT的算法子程序。分为第一级蝶形运算、第二级蝶形运算、第三级至7级蝶形运算3个部分编写程序。

（4）power：功率谱计算子程序。傅里叶变换的实部与虚部的平方和再开方就是功率谱。

4.2 仿真结果及其分析

在CCS3.3环境下对上述程序进行编译调试，仿真结果如图7、图8所示。

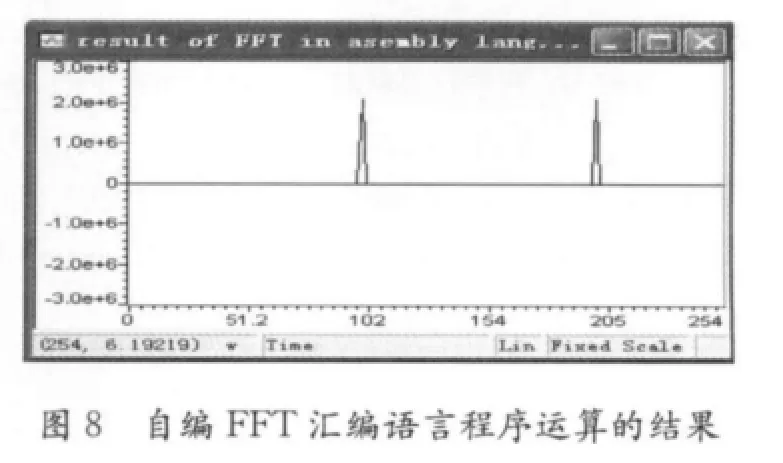
从图7和图8中可以看出，由CCS内部FFT 运算的结果与自编FFT 汇编语言程序运算的结果是一致的。

5 结束语

本文在阐述了实序列FFT 算法原理与过程的基础上，采用存储单元图方法在DSP TMS320C54X硬件资源及其汇编语言系统环境下对其算法公式进行了详细解析。给出了复序列FFT的实虚部各级算法的存储单元图，由复序列FFT 求其共轭对称与反对称的实虚部算法的存储单元图，以及由此求实序列的FFT的各级实虚部算法的存储单元图。在CCS3.3调试环境下的仿真结果说明了本解析方法的正确性。显然，存储单元图法不仅可以用来在其他汇编语言环境下解析FFT 算法，而且也可以用来对其他算法在汇编语言层面进行解析。

［1］QI Hua，LI Yong，HAO Chongyang.Designing and implementing a better real－time FFT module with block recursive a1gorithm ［J］.Journal of Northwestern Polytechnical Univer－sity，2009，7（2）：240－244（in Chinese）.［齐华，李勇，郝重阳.一种块递推实时FFT 算法模块设计与实现［J］.西北工业大学学报，2009，7（2）：240－244.］

［2］WAN Youhong，WANG Suoping.A kind of improved fast fourier transform（FFT）on DSP ［J］.Computer Engineering and Applications，2006，42（29）：84－86（in Chinese）.［万佑红，王锁萍.一种改进FFT 算法在DSP 上的实现［J］.计算机工程与应用，2006，42（29）：84－86.］

［3］LI Xin，LIU Feng，LONG Teng.Efficient implementation of fixed－point FFT on TS201［J］.Transactions of Beijing Institute of Technology，2010，30（1）：88－91（in Chinese）.［李欣，刘峰，龙腾.定点FFT 在TS201上的高效实现［J］.北京理工大学学报，2010，30（1）：88－91.］

［4］LIU Shu－tao，YANG Ping，KANG Hai－yan.The realization of FFT with C language based on improved repeat algorithm ［J］.Machinery ＆Electronics，2008，（2）：69－73（in Chinese）.［刘蜀韬，杨平，康海燕.基于改进重复算法的FFT 变换的C语言实现［J］.机械与电子，2008，（2）：69－73.］

［5］CHEN Fei，YUE Ning，WU Linfeng.A new FFT algorithm with real input and implementation in C language［J］.Information and Electronic Engineering，2008，6（6）：437－439（in Chinese）.［陈飞，岳宁，吴林峰.一种实序列FFT 新算法与C语言实现［J］.信息与电子工程，2008，6（6）：437－439.］

［6］Texas Instruments Inc.Implementing radix－2FFT algorithms on the TMS470R1x［EB／OL］.［2011－05－15］.http：／／focus.ti.com／lit／an／spna071a／spna071a.pdf.

［7］Texas Instruments Inc.A Block Floating Point Implementation on the TMS320C54xDSP ［EB／OL］.［2011－05－20］.http／／www.eeng.dcu.ie／～ee206／pdf／block＿flt＿pt.pdf.

［8］QIU Licun，WEN Wu，LIU Haiying.Discrete fourier transform on TMS320c54xseries DSP with DSPLIB ［J］.Control ＆ Automation，2005，21（7－2）：136－137（in Chinese）.［邱立存，闻武，刘海英.TMS320C54X 系列DSP 上FFT 运算的实现［J］.微计算机信息，2005，21（7－2）：136－137.］

［9］LU Wu，SHEN Ping，YI Jinghai.Implementation of fast fourier transform based on floating－point DSP ［J］.Modern Electronics Technique，2006，（3）：74－76（in Chinese）.［吕武，申萍，易景海.基于浮点DSP的快速傅里叶变换实现［J］.现代电子技术，2006，（3）：74－76.］

［10］ZHAO Hong－yi.DSP Technology with application examples［M］.2nd ed.Beijing：Electronic Industry Press，2010（in Chinese）.［赵红怡.DSP 技术与应用例［M］.2版.北京：电子工业出版社，2010.］

［11］CHENG Peiqing.Tutorial of digital signal processing（ition）［M］.3rd ed.Beijing：Qsinghua University Press，2007（in Chinese）.［程佩青.数字信号处理教程［M］.3版.北京：清华大学出版社，2007.］

［12］CHEN Hengliang，JIANG Yong.Design and realization of real FFT based on DSP ［J］.Journal of Dynamics and Control，2005，3（2）：50－53（in Chinese）.［陈恒亮，蒋勇.基于DSP的实数FFT 算法研究与实现［J］.动力学与控制学报，2005，3（2）：50－53.］