路网上的单色和双色反k最远邻查询

王宝文，彭 川，陈子军，刘文远

（1.燕山大学 信息科学与工程学院，河北 秦皇岛066004；2.河北省计算机虚拟技术与系统集成重点实验室，河北秦皇岛066004）

0 引 言

近年来空间数据库的研究备受人们关注，已成为一个热点研究领域。反最远邻查询是空间数据库理论与应用中的一类新问题。所谓反最远邻查询就是找到以给定的查询点作为其最远邻的目标点。它主要是解决根据给定点找到那些具有最小影响的点。而反最远邻查询的研究工作主要是在欧式空间下进行的，本文则是研究路网上的反k最远邻的查询问题。完善了反最远邻查询技术。

反最远邻查询的应用十分广泛。文献 ［1］给出了几个在欧式空间下反最远邻在现实生活中的应用。如化学工厂选址、避免同业竞争等问题。然而，在路网的环境下，反最远邻也有着其重要的应用价值。比如，在我们的日常生活中，消费者都喜欢到离他家近的商场去购买商品。除非有特殊原因，一般他们都不会去那些离他家很远的商场购物，即使那个商场的规模很大，商品很全，优惠或者活动很多。但那些大型商场的经营者肯定希望尽可能多的消费者去他们的商场购物。所以他们就要查找出哪些消费者离商场最远，最不可能到他们的商场来购物。找到这样的消费群体以后，采取一些有效的市场营销策略。比如在他们住的地方加大广告宣传力度，或者开通他们住的地方直达商场的购物班车等等。

在现实生活中，在路网环境下研究反最远邻则更接近我们的日常生活，本文就是将欧式空间的反最远邻扩展到了路网上，提出了在路网环境下的单色反k最远邻（MRkFN）和双色反k最远邻 （BRkFN）的定义和查询算法。经验证，反最远邻有着很重要的研究价值和重要意义。

1 相关工作

自从美国AT＆T实验室的Flip Korn和 Muthukrishnan.S［2］第一次提出反最近邻查询以来，数据库界对它给予了极大的关注。反最近邻查询目的是发现影响集，它的应用十分广泛，如决策支持系统、市场决策、资料库文件搜索、生物资讯、基于位置的服务、资源分配等方面都有着重要的应用价值。直至现在不管是在欧式空间下，还是在路网的环境下，都提出了很多有效的解决反最近邻查询的方法：基于预计算的方法、不需要预计算所有最近邻的60°裁剪法、完全不需要预计算的TPL裁剪策略等。另外，文献 ［3－7］提出了各种反k最近邻查询的解决方法，解决了单色和双色反k最近邻查询问题，连续反k最近邻查询问题等。Y.Tao等［8］人解决了在路网中的反最近邻问题。

而相对于反最近邻来说，反最远邻则是最近几年才逐渐成为研究的热点。它是在反最近邻查询的基础上提出的一个相对的概念。2009年李博涵，郝忠孝等人［9］提出了在明氏空间下利用离散边界点及邻域区等概念得到用于判定RFN的候选集的相关性质和定理，并给出其过滤算法。在得到过滤的候选集基础上，提出了F－RFN查询算法。2009年Bin Yao等人［1］提出了在欧式空间下的单色和双色反最远邻查询，并提出了一种新的查询算法，即采用了最远单元 （PFC）算法和凸包最远单元算法 （CHFC）来进行反最远邻的查询。这两种算法都采用了R－tree索引结构和使用了最远Vorionoi图来判断对象点是否是查询点的反最远邻。2010年Jianquan Liu等人［10］在Bin Yao提出的反最远邻查询算法基础上进行了改进和优化，提出了一种新的优化算法，有效地提高了查询效率，缩短了查询时间。在2009年Quoc Thai Tran等人［11］首次提出了路网上的反最远邻查询，他们主要是利用网络Vorionoi图和Dijkstra算法来查询路网上的单色反k最远邻，这种算法需要大量的预计算，而且查询效率也不高。然而本文提出的算法不仅不需要预计算，而且查询效率也有了很大的提高。

Quoc Thai Tran等人虽然首次提出了路网上的反最远邻查询，但他们并没有解决基于路网的双色反k最远邻查询问题。因为他们采用了Vorionoi图的思想来处理反最远邻查询问题，而使用Vorionoi图查找双色反最远邻时预计算占用的内存资源非常大。因此，文本采用转化的思想把反最远邻查询转化为反最近邻查询问题，利用反最近邻的查询方法解决反最远邻查询问题。

2 问题定义及性质

2.1 问题定义

在本文中，假设G（V，E）是带权的无向连通图，其中路网中的顶点的集合是V，边的集合是E，而在边集合E中，e为其中的一条边。顶点集合V中的个数为n。路网中对象点既有可能在路网的边上，也有可能在路网的顶点上。如果对象点在路网的边上，则需要做一个变化，把该边变成两条边，让对象点成为一个路网上的顶点。例如，p是路网上的一个在边 （u，v）上的对象点，则用 （u，p）和（p，v）替换 （u，v）。把p看成顶点加入V中。下面给出了相关的定义。

本文用dist（p，q）表示任意两个点之间的路网距离。

定义1 最短路径 （shortestPath）：已知带权无向连通图G （V，E），两个对象点p1和p2是路网G （V，E）的两个不同的顶点。p1和p2在路网上的最短路径就是p1与p2之间所有路径中路网距离最小的那条路径。

定义2 最远邻查询 （FN）：假设一个数据集P＝｛p1，p2，p3...，pn｝和一个查询点q，FN查询就是要找出P的子集FN （q），满足：FN （q）＝ ｛p∈P｜p′∈P：dist（p，q）≥dist（p′，q）｝。

定义3 k最远邻查询 （kFN）：假设一个数据集P和一个查询点q，kFN （q）是查询点q的k最远邻结果集，假设p∈kFN （q），则必须满足下面的条件

｜｛o∈P｜dist（o，q）＞dist（p，q）｝｜＜k

定义4 反最远邻查询 （RFN）：RFN与RNN的定义类似，给定一个数据集P和一个查询点q，RFN就是要找出P的子集RFN （q），满足：RFN （q）＝ ｛p｜p∈P且q∈FN （p）｝。

定义5 单色反k最远邻 （MRkFN）：单色反k最远邻查询就是查询点q与对象点p是相同的数据类型，找出数据集P的子集MRkFN （q），满足：MRkFN （q）＝ ｛p∈P｜q∈kFN （p）｝。

图1 单色反k最远邻 （MRkFN）

图1是一个单色反k最远邻的示例。给定数据集P＝｛p1，p2，p3…，p8｝和查询点q，且q和P中的点属于同一种类型。图1中有8个对象点，显然的2FN （q）＝｛p4，p8｝。然而，p8却不是q的单色反2最远邻，因为2FN （p8）＝ ｛p1，p2｝，所以，由定义5可知p8不是q的单色反2最远邻，而p1是q的单色反2最远邻，这是因为q∈2FN （p1）。这就说明了对象点p是查询点q的最远邻，但并不一定是q的反最远邻，反之亦然。根据定义4进一步判断可知，q的单色反2最远邻MR2FN（q）＝ ｛p1，p2，p3，p4｝。

定义6 双色反k最远邻 （BRkFN）：假设q∈Q，p∈P，Q和P是两种不同的数据类型。双色反k最远邻查询就是要找到数据集P的子集BRkFN （q），满足：BRkFN （q）＝ ｛p∈P｜q∈BkFN （p）｝。

图2 双色反k最远邻 （BRkFN）

图2是一个双色反k最远邻的示例。给定对象点集合P＝｛p1，p2，p3…，p6｝和查询点集合Q＝｛q1，q2，q3…，q6｝。由定义6可知，q1的双色反2最远邻BR2FN （q1）＝｛p6｝，因为p6的2最远邻2FN＝｛q1，q2｝，包含了q1。而q5的双色反2最远邻为空，因为对任意的pi∈P（1≤i≤6），

定义7 标记点［12］：所谓标记点就是假设G （V，E）是一个路网，q和p分别是路网上的查询点和对象点。而u是p和q之间的最短路径上的一点，若dist（u，p）＝dist（u，q），则u就称为标记p和q之间的标记点。标记点既可能在路网的边上，也可能在顶点上。

在本文中，若对象点和查询点之间存在多条最短路径，本文提出的算法会随机选择一条。因此也只能得到一个标记点。而且，位置相同的标记点在本文中会被认为是两个标记点。为了确保本文提出的算法的正确性，落在顶点上的标记点不计数。

2.2 问题性质

本文提出的算法的思想是把反最远邻查询问题转化为反最近邻查询问题。然后利用一些反最近邻的查询方法来处理反最远邻查询。假设数据集P＝ ｛p1，p2，p3…，pn｝和查询点q，要查找查询点q的反最远邻，换个角度思考就是要排除掉查询点q的相应的反最近邻。因此，通过这一转换，很多反最近邻的查询算法的研究成果就可以应用在反最远邻的研究中。根据这一转换思想，下面给出了两个定理：

定理1 如果p是q的单色反k最远邻，那么p一定不是q的单色反n－k－1最近邻。其中n是所有的兴趣点的个数。可形式化表示为：P＝ ｛p1，p2，…，pn｝，pi∈P，（1≤i≤n），q∈P

证明：

假设p∈MRkFN （q），对任意的p∈MRkFN （q），p是q的第i个反最远邻 （1≤i≤k）。由定义5可知，p的k最远邻包含q。因为q属于p的k最远邻，所以q肯定不是p的n－k－1最近邻。那么，

如图1所示，图1中有8个对象点和1个查询点，则总共有9个兴趣点。利用定理1找出查询点q的单色反2最远邻，即排除那些是q的单色反 （9－2－1）最近邻。进一步分析就是要找出哪些对象点的6最近邻不包含q，则这样的对象点就是我们要找的q的反2最远邻。图1中，p1的6最近邻6NN （p1）＝ ｛p2，p3，p4，p5，p6，p7｝，（p1）。所以，p1是q的MR2FN。同理，可找出q的单色反2最远邻结果集为 MR2FN （q）＝ ｛p1，p2，p3，p4｝。

定理2 假设P和Q是两种不同类型的点集，如果p是q的双色反k最远邻，且p∈P和q∈Q，那么p一定不是q的双色反n－k最近邻。其中n是Q中点的个数。即

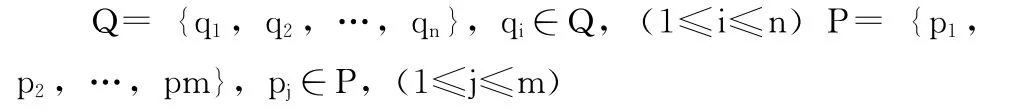
定理2的证明与定理1的证明类似。不同之处在于在转化的时候，单色反k最远邻是要排除查询点的单色反nk－1最近邻，而双色反k最远邻是要排除查询点的双色反nk最近邻。这是因为单色反最近邻查询时，查询点和对象点都属于同一种数据类型，考虑了查询点本身，而双色反最近邻查询没有考虑查询点本身，因为双色反最近邻查询查询点和对象点分别属于两种不同的数据类型。

如图2所示，图2中有两种类型的兴趣点，分别为P型点和Q型点。其中Q型点的个数为6。利用定理2找出查询点q1的双色反2最远邻。即排除那些是q1点的反 （6－2）最近邻的点。就是要找出哪些P型点的4最近邻的结果集里不包含查询点q1，则这样的点就是我们要找的q1的双色反2最远邻。图2中，p1的4最近邻4NN （p1）＝ ｛q1，q2，q3，q5｝。因为q1∈4NN （p1），所以由定理2可知p1不是q1的双色反2最远邻。而4NN （p6）＝ ｛q3，q4，q5，q6｝，q1不在p6的4最近邻的结果集中。所以p6∈BR2FN （q1）。最后，可求出BR2FN （q1）＝ ｛p6｝。由定理1、定理2可知，它们对欧式空间和在路网的环境下也都适用。

3 相关算法

3.1 路网上单色反k最远邻查询算法

本算法采用了定理1和标记点的思想，所谓标记点的思想［12］就是假设在查询点q和数据对象点p之间的最短路径边上总共有i个标记点，且i＞k，则p一定不是q的反k最近邻。

算法中首先找出路网上所有对象点和查询点之间的最短路径，然后在最短路径上找到标记点。最后根据落在对象点与查询点最短路径上的标记点的个数直接找到反k最远邻。具体算法如下：

算法1MRkFN算法／／求出给定查询点的单色反k最远邻

输入：路网G （V，E），查询点q，反最远邻数k

输出：查询点q的结果集Sr

算法1就是查找查询点q的单色反k最远邻。Sr是找到的反k最远邻的结果集。其中第3行利用了定理1中的转化思想，把反k最远邻查询转化为反n－k－1最近邻查询。然后再利用标记点的思想来查找反n－k－1最近邻。其中4行就是根据标记点的定义，利用Dijkstra算法求出了查询点与所有对象点之间的标记点。5－10行则是利用求出的标记点的个数直接找到查询点的反k最远邻。如果标记点的总个数大于k1，则直接把该对象点放入Sr中，否则放入Sc中有待进一步验证。11－13行就是验证Sc中的点是否是查询点的反k最远邻。

图3 单色反2最远邻示例

如图3所示，图3中有8个兴趣点，且都属于同一类型。令q为查询点，k＝2，则k1＝8－2－1＝5。首先利用Dijkstra算法找出查询点q与对象点之间的标记点mp1～mp7。然后计算各个对象点到查询点的最短路径上的标记点的总个数。p1，p2的marktotal为3，p3，p4的marktotal为4。只有p5，p6，p7的 marktotal为6大于5，则直接把p5，p6，p7放入Sr中，而把p1，p2，p3，p4放入Sc中需要进一步验证。经过进一步验证p1，p2，p3，p4不是q的反2最远邻。所以查询点q的单色反2最远邻最终结果为 ｛p5，p6，p7｝。

MRkFN算法的时间复杂度分析：假设n是路网中的顶点数，e是路网中边的条数。则Dijkstra算法的时间复杂度为O （（n＋e）logn）。MRkFN中第4行的时间复杂度为O（（n＋e）logn）。5－10行的时间复杂度是 O （n）。11－13行的时间复杂度是O （n（n＋e）logn），因为候选集Sc中的对象个数最多为n个。故算法1的时间复杂度是O （n（n＋e）logn）。

3.2 路网上双色反k最远邻查询算法

假设有两种不同类型的数据集Q和P，查询点q（Q。n为Q中所有点的个数。双色反k最远邻查询就是要找出在数据集P中以查询点q为它的最远邻的对象点的集合。双色反k最远邻查询算法跟单色反k最远邻查询算法有很多相似之处，不同之处是单色反k最远邻查询算法中k1的值为n－k－1（n是兴趣点的个数），而双色反k最远邻查询算法中的k1的值为n－k（其中n为Q中所有点的个数）。在用Dijkstra算法求最短路径的时候，双色反k最远邻查询算法不再是求查询点q与P中的对象点的最短路径，而是求查询点q与Q中其他点之间的最短路径，并做出标记点。

图4 双色反6最远邻示例

如图4所示，给出了一个双色反6最远邻的示例。图4中黑色的点表示Q类型的点，总共有10个。令q为查询点，k＝6，则k1＝n－k＝10－6＝4。先用Dijkstra算法分别找到查询点q与点q1～q9之间的最短路径，并在其最短路径上做上标记点mq1～ mq9。其中点q6到q的最短路径有两条，分别是 ｛q6，p7，q4，p4，q｝， ｛q6，q5，p4，q｝。遇到此类情况，算法会随机地选择一条最短路径来处理。在本例中算法选取 ｛q6，q5，p4，q｝作为q6到q的最短路径。然后分别求出q点到p1～p12的最短路径上的所有顶点的 markcount之和 marktotal。其中 p8，p9，p11，p12的marktotal都为5，即大于k1，所以直接把p8，p9，p11，p12放入Sr。把剩余的对象点放入Sc中，即Sc＝ ｛p1，p2，p3，p4，p5，p6，p7，p10｝。然后对Sc中的候选点进行验证。因为 B4NN （p3）＝ ｛q1，q2，q3，q4｝，q不 属 于B4NN （p3），所以p3也是q的反6最远邻。最后验证结果Sr为 ｛p3，p8，p9，p11，p12｝。

4 实验结果与分析

本节将测试本文所提出了MRkFN和BRkFN两种查询算法的性能和效率。测试中使用了加利福尼亚的路网数据和 building 类 型 的 数 据 点 集 （http：／／www.cs.fsu.edu／lifeifei／SpatialDataset.htm），其中加利福尼亚的路网数据中共包含21048个顶点和21693条边。｜building｜＝4110。测试中采用了模拟兴趣点的方式，随机地选择路网中某些结点作为查询点和兴趣点。每种算法都经过了30次测试，然后取得平均值得到的实验结果。

实验硬件环境为AMD双核2.21GHz的CPU，2G内存，软件环境使用Windows XP操作系统和VS2005开发环境。算法用C＋＋实现。

4.1 MRkFN实验结果与分析

如表1所示，我们根据兴趣点的个数把兴趣点分成了低、中、高3种不同的密度。兴趣点的个数小于30的是低密度，大于60的是高密度，在30和60之间的是中密度。如图5所示为随着k值的不断变化，3种不同密度下的MRkFN查询时间的变化。可以看出随着k值越来越大，MRkFN的查询时间越来越少。这是因为k值越大，则n－k－1的值就越小，就有可能有更多的对象点，它到查询点的的最短路径上的所有标记点的个数大于n－k－1。而且，还可以看出，高密度的兴趣点随着k值的变化最大。本实验说明本文提出的MRkFN算法适合查找兴趣点密度大，k值大的查询点的单色反k最远邻。

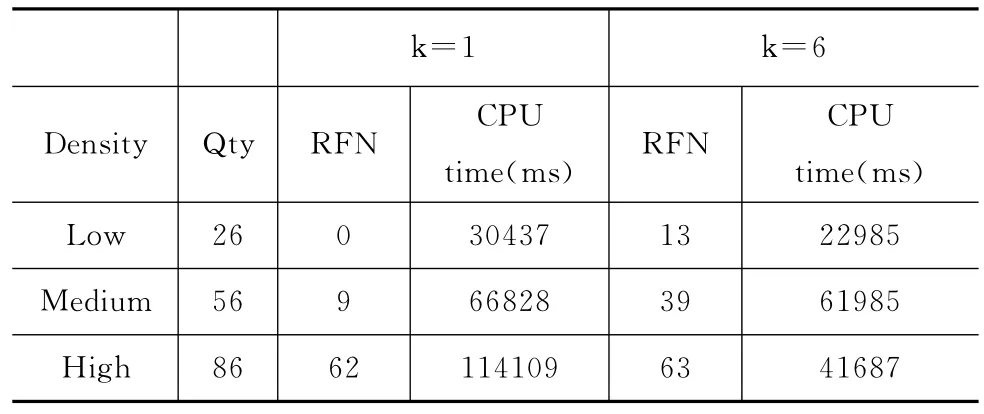
表1 k＝1和k＝6的实验数据

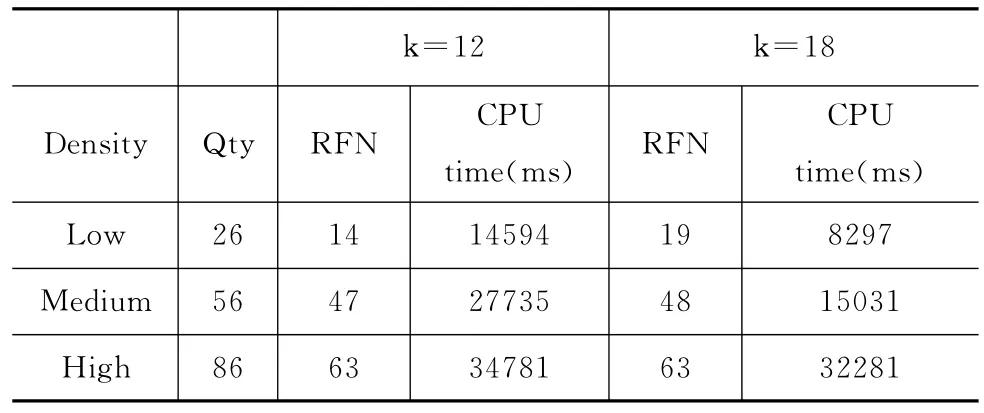
表2 k＝12和k＝18的实验数据表

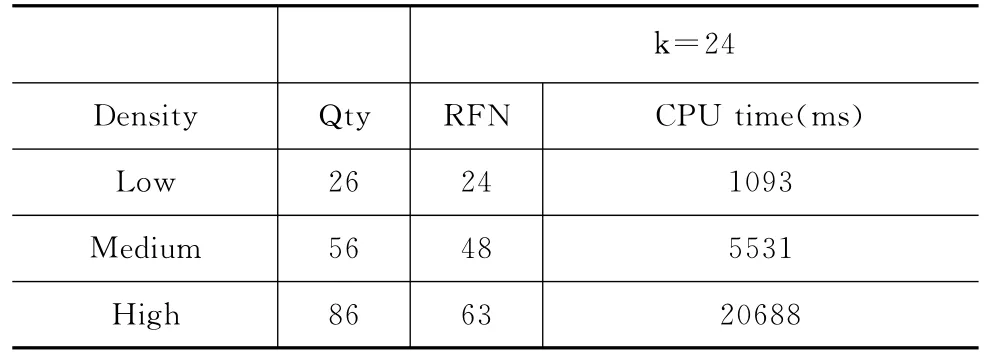
表3 k＝24的实验数据表

图5 兴趣点密度对时间的影响

4.2 BRkFN实验结果与分析

如图6所示，图6中两条曲线表示的是两种不同的BRkFN算法在不同的k值下的时间效率。朴素的BRkFN就是没有采用标记点的思想，直接用Dijkstra算法排除查询点的反n－k最近邻。可以看出随着k值的增加，本文提出的优化的BRkFN算法的优化效果就越明显。这是因为k值越大，n－k的值就越小，则通过标记点找到的反最远邻就越多。所以，查询时间就越少。

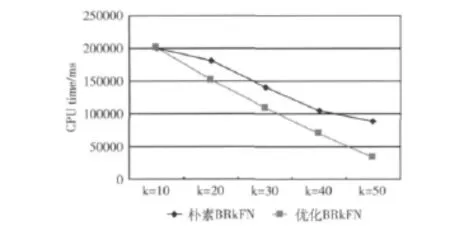
图6 BRkFN两种算法的比较

5 结束语

本文采用了转换的思想，从反最近邻的角度来思考分析和解决了反最远邻查询问题，把欧式空间下的反最远邻查询扩展到了路网上。提出了一种新的基于路网的单色反k最远邻和双色反k最远邻查询算法。完善了空间数据库中查询技术领域的理论研究工作。并通过实验验证了两种算法的有效性。在今后的工作中，我们将研究在路网的环境下，查询点是移动的或者对象点是移动的反最远邻查询。还有就是高维空间中的反最远邻查询算法的研究。

［1］YAO B，LI F，Kumar P.Reverse furthest neighbors in spatial databases ［C］.Proceedings of the IEEE International Conference on Data Engineering，2009：664－675.

［2］Korn F，Muthukrishnan S.Influence sets based on reverse nearest neighbor queries ［C］.Proceedings of the ACM SIGMOD International Conference on Management of Data，2000：201－212.

［3］James M Kang，Mohamed F Mokbel，Shashi Shekhar，et al.Continuous evaluation of monochromatic and bichromatic reverse nearest neighbors ［C］.IEEE 23rd International Conference on Data Engineering，2007：806－815.

［4］Muhammad Aamir Cheema，LIN Xuemin，ZHANG Ying，et al.Lazy updates：An efficient technique to continuously monitoring reverse kNN ［J］.Proceedings of the VLDB Endowment，2009，2 （1）：1138－1149.

［5］Mahady Hasan，Muhammad Aamir Cheema，Xuemin Lin，et al.Efficient construction of safe regions for moving kNN queries over dynamic datasets ［M］.The University of New South Wales Australia SSTD，2009：373－379.

［6］WU W，YANG F，CHAN C，et al.FINCH：Evaluating reverse k－nearest－neighbor queries on location data ［C］.Auckland，New Zealand VLDB，2008：1056－1067.

［7］WU Wei，YANG Fei，Chee Yong Chan，et al.Continuous reverse k－nearest－neighbor monitoring ［C］.9th International Conference on Mobile Data Management，2008：132－139.

［8］YIU M L，Papadias D，Mamoulis N，et al.Reverse nearest neighbors in large graphs ［J］.IEEE Transactions on Knowledge and Data Engineering，2006，18 （4），540－553.

［9］LI Bohan，HAO Zhongxiao.Efficient filtration and query algorithm of reverse furthest neighbor ［J］.Mini－Micro Systems，2009，30 （10）：1948－1951 （in Chinese）.［李博涵，郝忠孝.反向最远邻的有效过滤和查询算法 ［J］.小型微型计算机系统，2009，30 （10）：1948－1951.］

［10］LIU Jianquan，CHEN Hanxiong，Kazutaka Furuse.Hiroyuki kitagawa：An efficient algorithm for reverse furthest neighbors query with metric index ［G］.LNCS 6262：Berlin Heidelberg DEXA，2010：437－451.

［11］Quoc Thai Tran，David Taniar.Maytham safar：Reverse k nearest neighbor and reverse farthest neighbor search on spatial networks ［J］.Transactions on Large－Scale Data－and Knowledge－Centered Systems I，2009：353－372.

［12］CHEN Zijun，WANG Lu，LIU Wenyuan.Method for mutual nearest neighbor query in road networks ［J］.Mini－Micro Systems，2011，32 （4）：607－609 （in Chinese）.［陈子军，王璐，刘文远.路网中互近邻查询处理方法 ［J］.小型微型计算机系统，2011，32 （4）：607－609.］