一类两自由度碰振系统的胞映射计算

王 艳，刘冬芳，杨黎昆，殷一首

(1.军械工程学院基础部，河北 石家庄050003;2.军械工程学院二系，河北石家庄050003)

近年来国内外学者主要利用理论推导和计算机数值模拟相结合的方法研究了碰撞振动系统的动力学行为[1－4]。Hsu C.S[5]提出了胞映射数值计算方法，这种方法把状态空间中的每个状态变量按等间隔划分成胞，以胞的中心点的特性代表整个胞的特性，通过对中心点进行连续的poincare映射，完成对所研究区域的全局分析。胞映射法使非线性动力学内在的复杂性通过相空间转换而清晰地展现出来，只要计算机的速度和内存容量允许，对高维非线性动力学系统都能够以任意尺度来划分胞并进行胞映射全局性态分析。目前这种方法已被应用于进行单自由度碰撞振动系统的全局分析[6]，但尚未见将此方法应用于研究多自由度碰撞振动系统的全局性态。

本文对一类两自由度碰撞振动系统的全局性态进行了分析，发现了在一定参数条件下存在的共存吸引子现象，进而结合胞映射方法和poincare映射，计算得出了系统单周期运动的吸引域，并给出了吸引域范围随外加激振频率变化的趋势。

1 两自由度碰振系统的力学模型

图1是一个两自由度振动系统与固定约束发生碰撞的力学模型。质块M1和M2分别由刚度为K1，K2的线性弹簧和阻尼系数为C1，C2的线性阻尼器连接。质量为M1和M2的质块的位移分别用X1和X2表示。作用在质块M1和M2上的激励振幅为P1和P2，频率为Ω的简谐激励Pi sin(ΩT+τ)(i=1，2)。当质块M1位移X1等于间隙B时，质块M1将与刚性约束A碰撞，改变速度方向后，又以新的初值运动，然后再次与约束A碰撞，如此往复。假设力学模型中的阻尼是Rayleigh型比例阻尼，碰撞过程由碰撞恢复系数R确定，碰撞持续时间略去不计。在任意连续两次碰撞之间，振动系统的运动微分方程为

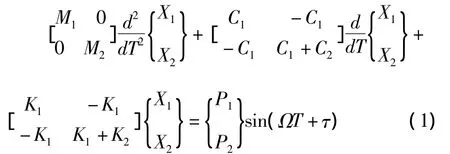
质块M1的冲击方程为

方程(1)和(2)的无量纲形式为

在方程(3)和(4)中，“﹒”表示对无量纲时间t求导数，其中无量纲量为

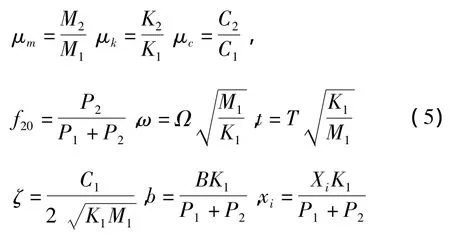
建立碰振系统的Poincare映射。

2 系统的全局分析

选取一组无量纲系统参数为μm=2.0，μc=4.0，B=1.2，f20=0.0，C=0.0，R=0.7，取激振频率ω为分岔参数，图2给出了外加激振频率ω∈[0.6～0.7]范围内变化时系统的全局分岔图。由于初始值不同或受到扰动，系统存在如图2(1)、(2)所示的两个不同周期运动的全局分岔图。

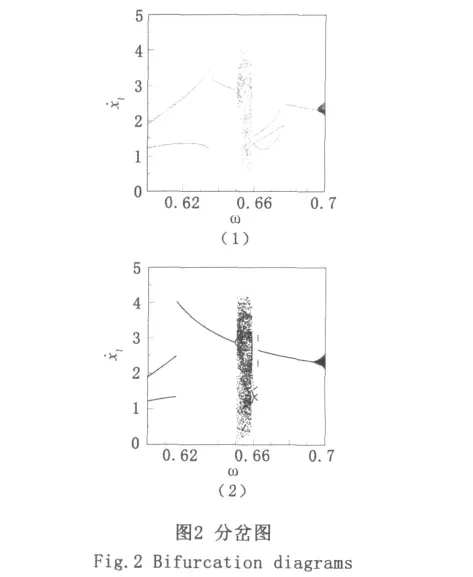
图2(1)显示系统约在ω∈[0.6，0.635 5]范围内具有双周期运动，当激振频率递增穿越ω≈0.636时，系统由双周期运动突变为单周期运动，激振频率继续增大，周期运动失稳，约在ω∈[0.651，0.658 5]区间内系统表现为混沌运动。随着激振频率的进一步增加，系统退出混沌状态，呈现出稳定的周期3运动。而ω增大至约0.678时，系统转化为单周期运动。随着激振频率的增大，在ω≈0.693 5单周期运动发生hopf分岔，形成概周期运动，概周期运动失稳后转迁为混沌运动。图3(1)～(8)是系统随外加激振频率的增加运动状态的演化过程。

图2(1)与(2)对比发现，当初始值不同或受到扰动时，系统在某个激励频率范围内会存在多吸引子共存的现象。在ω≈0.616 5至ω≈0.635 5区间内，系统存在单周期运动和双周期运动共存的现象，在ω≈0.662至 ω≈0.678区间内，则存在单周期运动和三周期运动共存的现象。

3 周期运动吸引域的胞映射计算

胞映射法认为，点映射系统只是从理论上将状态空间看成是连续的，而实际总会有一个步长。当所找的点与理想点的距离小于这个步长时，就认为它们是同一点。这样也就是说，状态点可以用有限大小的单元－胞来表征。在胞映射思想的基础上，结合变步长积分法，对图1所示两自由度碰撞振动系统周期运动的吸引域进行计算。先结合文献[7]利用点映射和胞映射相结合的方法，求出系统周期运动在Poincare截面上的不动点及其周期数(不动点的个数)。然后将研究区间细分为一定数量的胞，取每个胞的中心点作为初始迭代点进行点映射计算，求得其在Poincare截面上的映射点，如果映射点仍然落在研究区间内，记下映射点所在的胞，从而建立起胞与胞之间的映射关系，如果经过有限次迭代，系统收敛于不动点所在的胞，则这个胞就是系统周期运动吸引域中的一个胞。计算完研究区间里的所有胞，经过对映射的分析就可以得到系统周期运动吸引域的范围。

选取一组无量纲系统参数为μm=2.0，μc=4.0，B=1.2，f20=0.0，C=0.0，R=0.7，ω =0.662，在一定的初始条件下，系统具有单周期运动，在Poincare截面上表示为不动点(1.2，2.650 3，0.196 6，0.096 4，1.377 9)。给初始条件一些扰动，系统可能发生周期三运动，在Poincare截面上表示为三个不动点，求得其中一个不动点为(1.2，1.392 1，0.541 9，－2.345 9，1.188 2)。

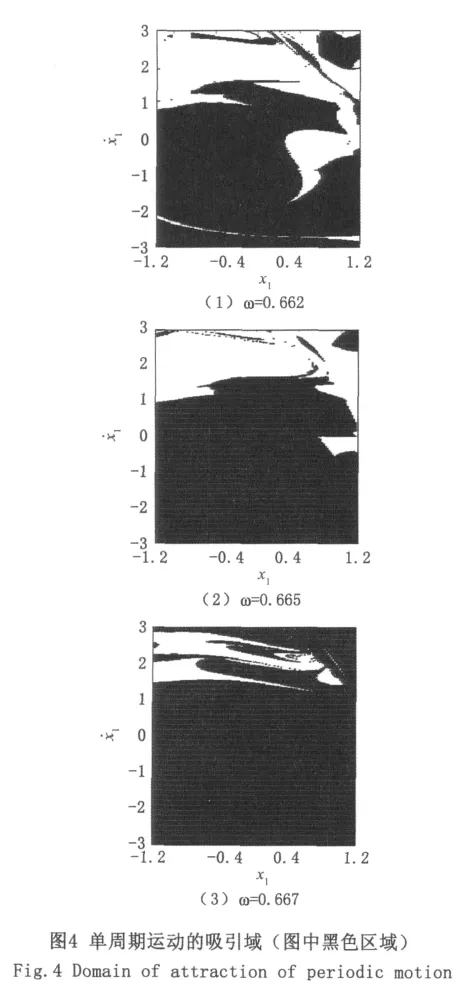
将研究区间划分为300×120个胞，经过计算求得收敛于单周期运动的胞有24 027个，占总胞数的66.7%，系统单周期运动的吸引域如图4(1)中的黑色区域，在此区域内任选一点作为初始迭代点，系统最终都可以稳定在期望的单周期运动轨道上。系统其他参数保持不变，增大外加激振频率ω，单周期运动的吸引域面积逐渐增大如图4(1)～(3)。当ω=0.665时，收敛于单周期运动的胞有26 850个，占总胞数的74.6%。当 ω=0.667时，收敛于单周期运动的胞有32 079个，占总胞数的89.1%。经计算，当将外加激振频率增大至ω≈0.678时，收敛于单周期运动的胞有36000个，占总胞数的100%，正符合系统的全局分岔图显示的信息ω≈0.678时，系统完全表现为单周期运动见图2(1)。

4 结论

在设计碰撞机器时，最重要的是使机器工作在稳定的周期运动中。为了便于设计，一种切实可行的方法是:通过分析单周期运动的稳定性和局部分岔来获得分岔图。分岔图能够使我们在稳定性前提下选取合适的参数，使单周期响应发生在所期望的位置。本文基于胞映射思想，采用变步长积分法，通过计算得出了一类两自由度碰撞振动系统单周期运动的吸引域图，在吸引域范围内任选一点作为初始迭代点，系统最终都可以稳定在期望的单周期运动轨道上，这就为碰撞振动机械系统的动力学优化设计、可靠性及降低噪声提供了理论依据，对涉及碰撞振动和机械间隙的广泛领域都有积极的实际意义和运用价值。

[1]罗冠炜，谢建华.碰撞振动系统的周期运动和分岔[M].北京:科学出版社，2004.

[2]吕小红，朱喜锋.一类冲击钻进机械系统的动力学特性[J].振动与冲击，2011，30(6):239－242.

[3]李群宏，陆启韶.一类双自由度碰振系统运动分析[J].力学学报，2001，33(6):776－ 786.

[4]扬振中.小型振动冲击式打桩机动力学性能研究[J].农业机械学报，1999，30(6):36 － 40.

[5]HSU C S.Cell－to－cell mapping:a method of global analysis for non－linear system[M].New York:Springer Verlag，1987.

[6]HSU C S.A gerenalized theory of cell－to－cell mapping for nonlinear dynamical systems[J].ASME J.Appl.，Mech.，1981，48:634 －642.

[7]李 健，张思进.非光滑动力系统胞映射计算方法[J].固体力学学报，2007，28(1):93 －95.