水泥石膏材料相似模拟节理岩体有限元分析
王永亮,栗东平
(1.清华大学土木工程系,北京100084;2.河北工程大学 工程力学系,河北邯郸056038)
实际工程中,现场岩体体积庞大,实际岩体强度的检测难以实现,且测试费用较高,进而发展了在实验室中利用小尺寸试件来模拟实际岩体的分析方法[1],这就需要发展相应的相似理论[2-3]和相似模型。文[4]中利用水泥石膏材料来相似模拟岩体,通过实验室大量的模拟试验得到了模拟砂岩的配合比,显示了该水泥石膏材料良好的性能。在该复合砂浆中,水泥作为粒状浆材,可以提高复合砂浆的强度;石膏粉能调节复合砂浆的胶结时间。因此,该复合砂浆不但保留了水泥砂浆流动性好等优点,而且克服了水泥砂浆强度低的弱点,它大幅度提高了砂浆的抗压强度和抗剪强度[5],具有优良的复合性能,是一种较好的相似材料。
岩体是由岩块和结构面组成的地质体,因此其强度必然受到岩块和结构面强度及其组合方式的控制。一般情况下,岩体的强度不同于岩块的强度,也不同于结构面的强度,如果岩体中结构面不发育,呈完整结构,则岩体强度大致等于岩块强度,如果岩体将沿某一结构面滑动时,则岩体强度完全受该结构面强度的控制[6]。这两种情况,相对比较好处理;本文将着重讨论被节理切割的裂隙(节理化)岩体强度的确定问题。它一方面受岩石材料性质的影响,另一方面受结构面特征(数量、方向、间距、性质等)和附存条件(地应力、水、温度等)的控制。本文将进一步利用上述水泥石膏材料相似模拟三维岩体,进行有限元分析,研究其不同节理倾角下的抗压强度。
1 相似试验研究
试验原料水泥:42.5普通硅酸盐水泥;石膏:特级熟石膏粉;硼砂:采用工业用硼砂(一等),硼砂含量>95%,在试验中加入的硼砂浓度为1%;砂:模数为2.7的河砂(中砂)。
为了研究骨料对水泥石膏模拟材料性能的影响,做了固定水泥用量(200 g)和石膏用量(150 g),逐渐增大砂用量的室内试验,并在此基础上绘制了随砂含量的增大,水泥石膏模拟材料的抗压强度、抗弯强度、弹性模量的变化曲线。随着砂量的增大,水泥石膏模拟材料的抗压强度和抗弯强度在小范围内显著减小。固定砂用量(1 900 g)和石膏用量(120 g),研究水泥用量对水泥石膏模拟材料性能的影响。当固定砂和石膏用量时,水泥石膏相似材料的抗压强度和抗弯强度在小范围内随水泥用量的增大呈明显增大的趋势。固定砂用量1 900 g、水泥用量200 g时 ,逐渐增加石膏的含量,研究石膏用量对水泥石膏模拟材料性能的影响。当固定砂和水泥用量时,水泥石膏相似材料的抗压强度和抗弯强度在小范围内随石膏用量的增大呈明显的增大趋势。水胶比也是影响水泥石膏模拟材料的一个重要指标。当固定砂、水泥和石膏的用量时,水泥石膏模拟材料的抗压强度和抗弯强度在小范围内随着用水量的增大呈明显减小的规律。
在上述试验分析结果的指导下,进行了相关试验,得到模拟材料的抗压强度范围为2.10 MPa~6.30 MPa。
2 相似模型的有限元分析
2.1 有限元分析概述
分析强度问题,运用理想弹塑性模型[7-8]即可获得比较精确的解答。摩尔-库伦(M-C)屈服准则可很好地描述大多数岩土材料的强度特性[9-10],因此本文采用M-C屈服准则。由于M-C屈服准则的屈服面为不规则的六角形截面的角锥体表面,存在尖顶和棱角,给有限元计算带来很大的不便,为此需要修正。本文中所用软件ANSYS采用的是广义Mises准则[11],其通式为
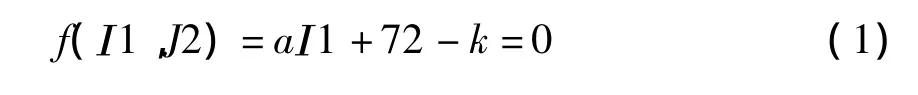
式中a、k为与c、φ有关的参数,变换a、k值就可在有限元中实现M-C系列修正的屈服准则。
从式(1)看,在平面应变条件下,M-C内切圆屈服准则采用关联流动法则时与M-C屈服准则是一致的[12],有很高的计算精度,因此本文选择M-C内切圆屈服准则作为岩块的屈服准则。
合理地分析和模拟节理的力学特性和破坏机制一直是工程界和学术界关注的热点问题[13-15]。本文基于有限元软件ANSYS,拟采用夹层模型来进行节理的数值模拟。假设结构面有一定的厚度(即岩块中存在夹层),采用与水泥石膏岩块相同的常规实体单元,本构关系与屈服准则也与其一致,只是强度参数(粘聚力c、内摩擦角φ等)有所不同。
下面将通过对 0°、30°、45°、60°等各个角度的节理岩体进行模拟,进而得到各自的抗压强度。对于各个角度模型的有限元分析具体步骤类似,下面主要讨论45°情况,其它各模型类似讨论可得相应结果。
2.2 45°倾角试块的有限元分析
根据ANSYS采用SOLID65单元来模拟所选用的材料,建立30 mm×30 mm×60 mm的立方体几何模型。节理的厚度为短边边长的1/20,即1.5 mm,这条单节理与水平面成45°夹角。将立体沿各个划分后的长边分成4份,短边分成2份的有限元网格划分方法,具体模型如图1所示,参数设置见表1、表2。

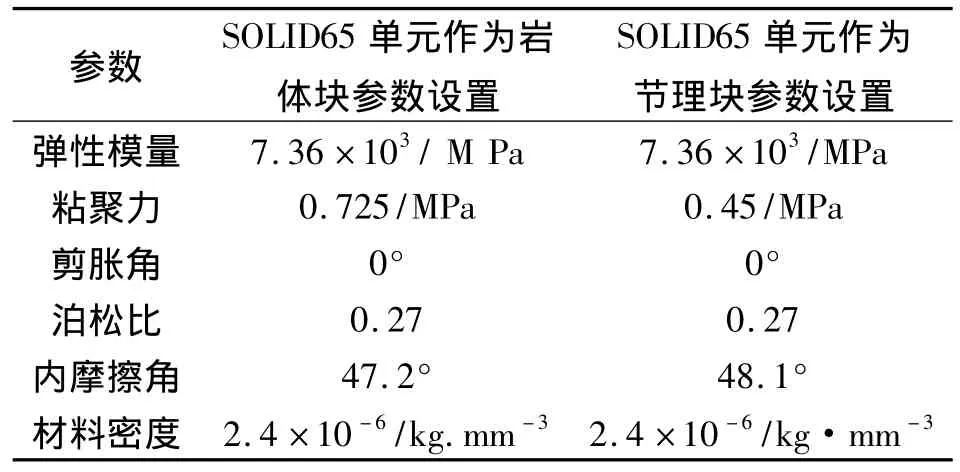
表1 SOLID65单元参数Tab.1 SOLID65 parameters

表2 岩体块与节理块接触对参数Tab.2 Rock blocks and joints contact parameters
根据试验室的实际加载情况,考虑到试验机的压头对试块上下两个面在各自平面内进行约束,因此,可将模型底部面上的各节点在X,Y、Z方向的位移进行约束,将顶部面上的节点在X、Z方向的位移进行约束。为了保证压力均匀,在试件顶部面上的Y方向施加10.0 MPa的压力载荷,在求解过程中,打开自动时间步,即可自动选择合适的荷载步增量,逐步加载到试件的顶部。在分析计算过程中,不考虑温度的影响,采用力收敛和位移收敛相结合的收敛准则,打开线性搜索选项,输出每一步的计算结果,打开程序的自动二分选项,设置终止时间为1,设置50个子步,每一个子步的不平衡迭代次数为35步,每个载荷子步结果都输出到结果文件中。
结果后处理分析:通过对30 mm×30 mm×60 mm尺寸的试件进行模拟计算,可以得出随着载荷步和时间的增加,载荷与位移(Y轴方向)的数据。当时间进行到 Time=0.648 47时,结构破坏,程序由于不收敛而结束计算,得出相应荷载-位移曲线,如图2所示。
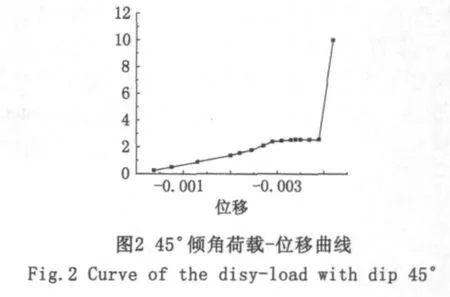

由图2可以看出,荷载-位移变化关系基本上分为三部分:第一部分0-2.414 47阶段,这一阶段曲线基本成直线,而且曲线的斜率基本比较陡;第二部分2.414 47-2.561 57阶段,这一阶段曲线的变化基本比较平缓;第三阶段2.56157-10.000 00阶段,这一阶段,曲线就是一条直线。从图2上可以看出:首先是节理面的上力所产生的变形,在这一阶段模型的变形基本以弹性变形为主,第一段斜直线部分,然后是节理面尖端产生的变形,最后为产生裂纹,并且这一阶段最明显的特征为,位移持续增大,而荷载变化很小,如图2中间平缓部分,在这一阶段末和下一阶段初,模型失去承载力,因此可以认为,第二阶段末和第三阶段初所对应的荷载即为这一尺寸试件的极限荷载,即Pmax=2.561 57 MPa。这也正好和试验室中试块的破坏形式基本上一致。模型受力过程中,从不同子步应力变化可以看出:随着荷载的加大,模型的节理附近的应力变大,这与试验中对应试块的裂纹在中部节理部位产生的现象相吻合,如图3所示。当 substep=14,t=0.648 47时,变形急剧增大,也表明节理岩体达到了其极限载荷。
2.3 0°、30°、60°倾角试块的模拟分析
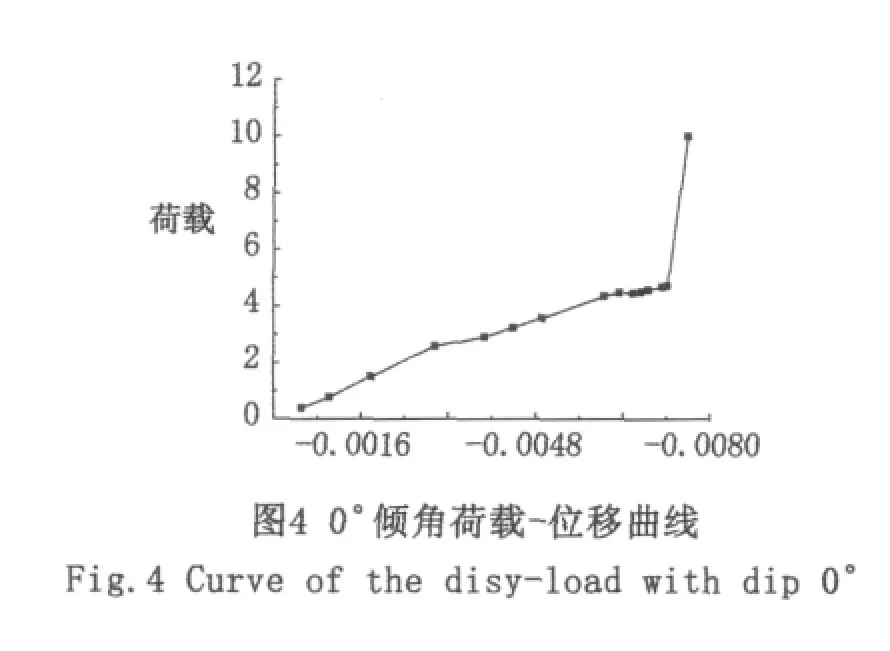
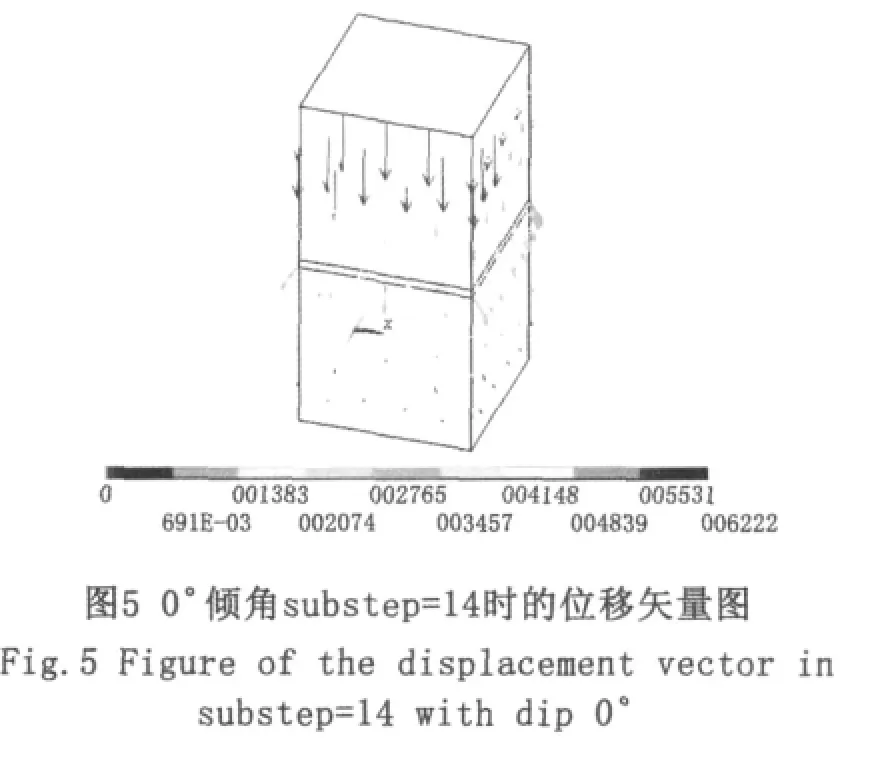
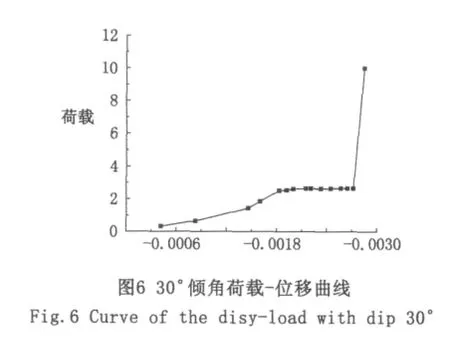
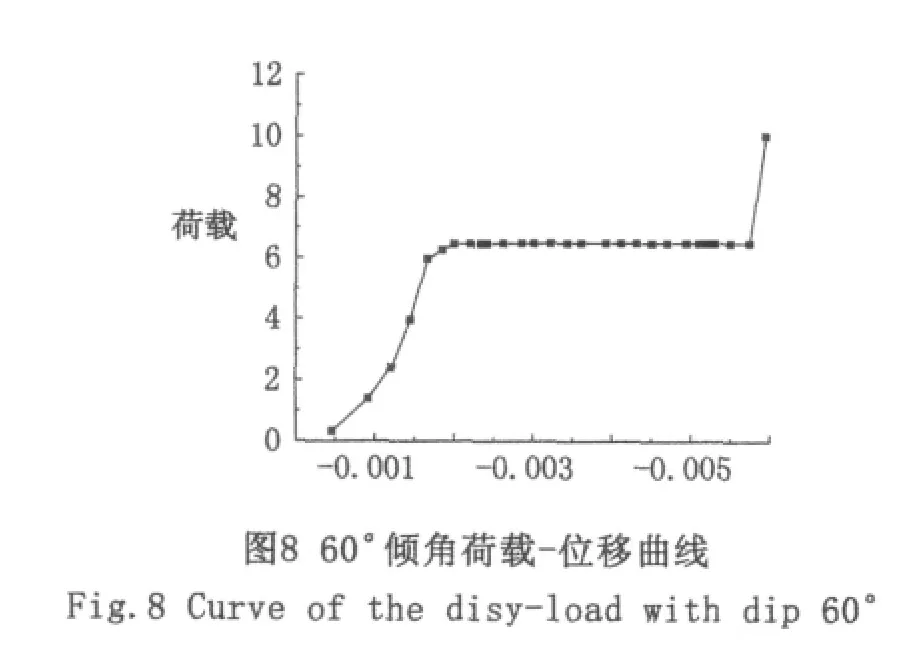
当倾角为0°时,时间进行到 Time=0.777 35时,程序由于不收敛而结束计算,得出荷载-位移曲线,如图4所示。第二阶段末和第三阶段初所对应的荷载即为这一尺寸试件对应的极限荷载,即Pmax=4.720 69 MPa。如图5所示,当 substep=14时,对应模型中部的应力出现大面积变大,由此可以断定当t=0.777 35时对应的荷载即为其极限荷载;并且,由位移矢量也可以看出t=0.777 35时,变形急剧增大,也表明节理岩体达到极限载荷。同理,30°、60°倾角情况,极限荷载分别为Pmax=2.655 61 MPa、Pmax=6.488 86 MPa,分别如图6、图7、图 8、图 9 所示。


3 抗压强度与有限元果分析
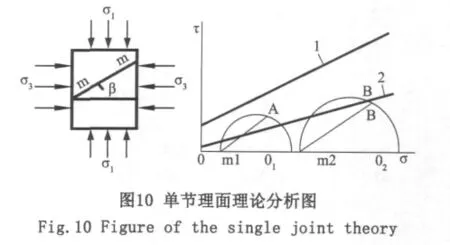
为了从理论上用分析法研究裂隙节理的抗压强度,耶格(Jaeger)提出了单结构面理论。单节理面理论分析如图10所示。
岩体中发育一组结构面AB(m-m),假定AB面(指其法线方向)与最大主应力方向夹角为β,由莫尔应力圆理论,作用于AB面上的法向应力σ和剪应力τ为
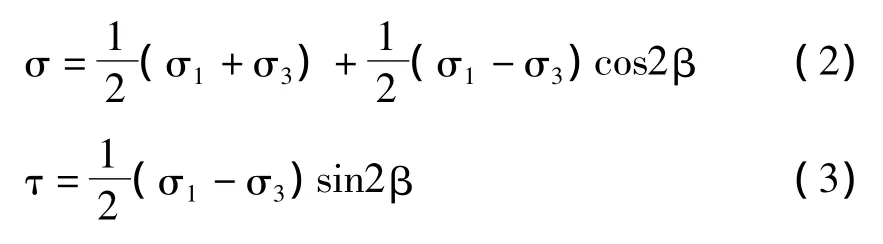
结构面强度曲线服从库伦准则

式中cω,φω分别为结构面的粘结力和内摩擦角。
文[16]中采用PLANE42单元,与本文同样利用夹层模型来模拟单节理岩体,建立平面模型,得到节理在不同倾角下岩石地基的承载力值。结合上文得到的单节理岩体抗压强度模拟值和理论值,可以得出三者在节理倾角变化时的数据汇总,如表3所示。

表3 各抗压强度随倾角的变化Tab.3 Every intensity of pressure with the change of the angle
根据表3中数据可以得到倾角-抗压强度曲线,如图11所示。由图11可以看出:
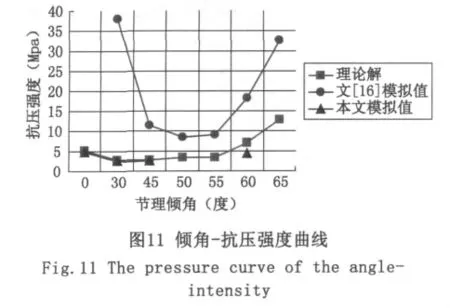
1)本文水泥石膏相似模型的抗压强度与理论值十分接近,可以认为建立该相似模型是符合实际情况的。
2)将本文有限元分析结果与理论值、文[16]结果进行比较、分析,可以看出三者的变化趋势是相同的,即单个节理岩体的抗压强度并不是随着该节理倾角的变化而单调递增或递减,而是随着倾角的逐渐增加,抗压强度先是逐渐减少到一个最小值,而后逐渐增加。
3)文[16]中所得到的强度值均比理论值和本文的模拟值明显偏大,是因为其所用的参数完全是岩体的实际参数,建立的平面模型,模拟的是真实的岩体。而本文中用到的参数是根据实验室中模拟岩体的水泥石膏试块所具有的参数来确定的,建立的是三维实体模型,理论值也是根据该参数来进行求解的,所以理论值与本文模拟值相近。若调整水泥石膏材料中的用料配比,也可以对文[16]中的真实岩体进行模拟。
4 结论
1)其承压破坏方式与实际节理岩体破坏方式相似,进而验证了水泥石膏相似模拟岩体的可行性。
2)本文仅考虑单节理的岩体强度,实际岩土工程中更多的是多节理的岩体,相应分析也会更加复杂。岩体的强度不单单与节理倾角有关,还与岩石强度、节理位置、周围环境等等有关。对于水泥石膏模拟岩体,也应当进一步考虑模型的尺寸效应。
[1]林韵梅.实验岩石力学-模拟研究[M].北京:煤炭工业出版社,1984.
[2]左保成,陈从新,刘才华.相似材料试验研究[J].岩土力学,2004,25(11):1805- 1808.
[3]彭海明,彭振斌,韩金田.岩性相似材料研究[J].广东土木与建筑,2002,12(12):13-17.
[4]栗东平,王谦源,张增祥,等.模拟岩性的相似试验研究[J].河北工程大学学报:自然科学版,2007,24(2):12-19.
[5]黄戡,卿凇,谢国柱.水泥石膏相似材料的模拟实验[J].西部探矿工程,2003,15(12):127-129.
[6]GHOSH A,DAEMEN J J K.Fractal characteristics of rockdiscontinuities[J].Engineering Geology,1993(34):1-9.
[7]赵德安.节理塑性对岩体性能的影响分析[J].兰州铁道学院学报,2002,21(4):1 -4.
[8]ZHAO DEAN.Impact of joint plasticity to properties of rock mass[J].Journal of Lanzhou Railway University(Natural Sciences),2002,21(4):123-127.
[9]蔡美峰,何满潮,刘东燕.岩石力学与工程[M].北京:科学出版社,2002.
[10]李晓红,王成.含节理的岩石地基承载力估算[J].工程力学(增刊),2001:659-662.
[11]WU JIMIN,A.MABTAB,XU SHULIN.Estimation the barton equation for the shear strength of rock joints[J].Journal ofEngineeringGeology;2007(04):0349-0353.
[12] CARPINTERI A.Scaling law and renormalization groups for strength and toughness of disordered materials[J].International Journal of Solids and Structures,1994(31):610-613.
[13]张志刚,乔春生,刘勇.节理岩体强度特征研究综述[J].煤田地质与勘探,2006,34(5):38-41.
[14]张志刚,乔春生,李 晓.单节理岩体强度试验研究[J].中国铁道科学,2007,28(4):34 -39.
[15]张志刚,乔春生.改进的节理岩体强度参数经验确定方法及工程应用[J].北京交通大学学报,2006,30(4):46-49.
[16]邓楚键,孔位学,郑颖人.节理岩石地基极限承载力的有限元分析[J].工业建筑,2005,35(12):51-54.

