大容量动力铅酸蓄电池建模方法

杨占录 张国庆 王宗亮

（海军潜艇学院，山东青岛 266042）

0 引言

随着传统能源供应的日益紧张以及人们环保意识的提高，各大汽车制造商竞相推出或准备推出电动汽车。大部分电动汽车使用大容量动力电池，其中就有铅酸蓄电池。所有电动汽车都有电池管理系统（BMS），BMS对电池的当前状态进行检测，并根据使用情况对未来的状态做出预测，这就需要建立蓄电池的数学模型。本文介绍几种常见的蓄电池模型建立方法。

1 基于电化学机理的建模方法

蓄电池内部电解液所含有的活性物质，其浓度损失百分比可表示为：

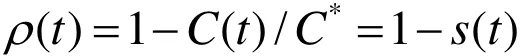
式中：C*为初始浓度；C(t)为电解液中t时刻活性物质的浓度；时间t的取值范围[0，L]，L为放电总时间，s(t)为t时刻的荷电状态SOC。

当使用蓄电池一维的电化学模型，根据电化动力学理论，最终可得到电解液活性物质浓度损失百分比函数：

式中：v为反应中电子的数目；F为法拉利常数；A为电极的面积；D为扩散系数。

若考虑电流值为I的恒流放电过程，放电截止时ρ(L)=1，则可以得到以下等式：

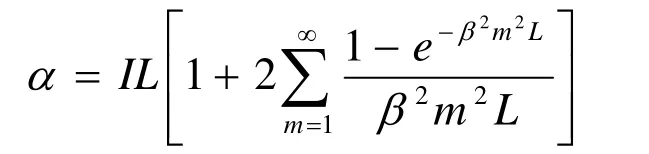
对于给定的恒流放电集合{I*，*=1，2，…，n}，可以使用最小二乘法得到最优的α、β参数，进而计算ρ(t)、s(t)，其中：

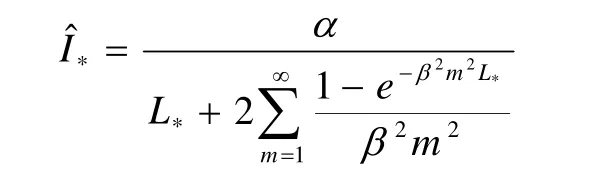
蓄电池机理建模侧重于蓄电池的理论研究和设计，需要较强的电化学理论知识和设计经验，蓄电池电化学机理模型和实际情况有较大差距，侧重于理论验证，一般用于蓄电池的辅助设计。

2 基于电化学经验公式的建模方法

电化学专家根据电化学理论分析和实验数据进行拟合分析，得出一些经验公式，根据这些经验公式的推导和分析，预测蓄电池电气外特性和剩余容量，从而形成了电化学经验公式模型。

2.1 Peukert经验公式、Shepherd方程

Peukert经验公式为：

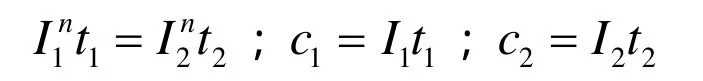
Shepherd方程为：

式中：I1、I2为放电电流，t1、t2、C1、C2为以相应电流恒流放电的放电截止时间和放出的电量，U为蓄电池端电压，ES、Ri、Ki、A、B、C均为恒定系数，可根据实验数据获得。

在恒流放电条件下，Peukert经验公式可以对容量进行估算，Shepherd方程可以对蓄电池端电压进行估算，这两个方程联立求解，即可得出不同荷电状态下蓄电池的电气外特性。

2.2 Nernst方程和Tafel方程电池模型

将Nernst方程表现为半经验公式形式：

式中：a、b—经验常数；E—蓄电池电动势；Q—蓄电池电量；i⋅ t—蓄电池放电量；t—放电时间。

Tafel方程表现为经验公式形式：

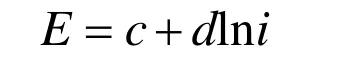
式中：c、d—经验常数；i—蓄电池放电电流。蓄电池电流则由下式表现：

式中：I—蓄电池总电流。

由以上三式可推导经验常数的计算式：

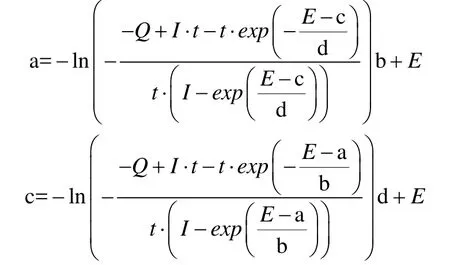
以上四个参数可由蓄电池的放电性能曲线初步判定，可利用所推导的计算式反复校对经验值的准确性，以提高模型的计算精度[6]。

3 基于等效电路的建模方法

3.1 Thevenin等效电路

Thevenin等效电路采用直流电压源E与内阻r串联，并与阻容并联网络串联，阻容网络表示蓄电池的过电压现象，在蓄电池两端并联电阻Rg表示自放电现象，其电路原理图如图1所示。各元件的参数随蓄电池的状态（如荷电状态、温度）的变化而动态变化，变化规律的辨识与电化学经验公式模型的处理方法相同。由于等效电路模型考虑的动态过程更加具体，所以其参数辨识也更加困难，如表示过压现象的阻容网络，其电容、电阻值的辨识准确度很难提高。

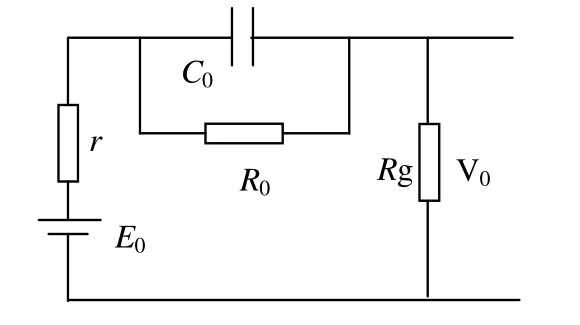
图1 Thevenin等效电路

根据电路定律可得到：

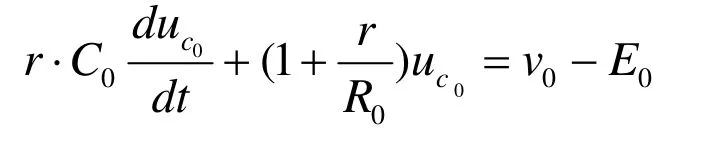
式中：E0—理想电压源；r—内阻；C0—平行极板之间的电容；R0—极板与电解液之间的非线性接触电阻。

3.2 PNGV模型

PNGV等效电路电池模型通过对电池参数的线性化处理来模拟电池在一定 DOD水平下的动态性能。这个线性的等效电路模型能较好地预测电池在 HPPC测试循环下的电池端电压[5]。模型的等效电路和数学公式描述如下所示。

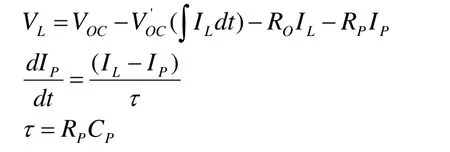
式中： VOC—理想电压源，它表示的是电池的开路电压； 1 /—该电容描述的是因电流的时间积分而引起的开路电压的变化；RO—电池的欧姆内阻； RP—电池内部极化电阻（如由于浓差极化）； CP— RP的并行电容；τ—极化时间参数；IP—极化电阻的电流； VL—电池端电压。

图2 PNGV等效电路

4 基于神经网络的建模方法

由于人工神经网络具有逼近多输入输出参数函数的特点，使其可以估计电池在不同放电状态下所能够放出的容量。

4.1 基于BP神经网络的建模方法

BP神经网络是一种单向传播的多层前向网络，它除了有一个输入层和一个输出层外，还有一层或多层的隐层，同层节点中没有任何耦合。输入信号从输入层节点依次传过各隐层节点，然后传到输出节点，每一层节点的只影响下一层节点的输出。BP神经网络具有的非线性映射能力保证其能够成功逼近各种非线性函数。另外，BP神经网络将信息分布式存储于连接权系数中，使网络具有较高的容错和鲁棒性。因此在目前的人工神经网络的实际应用中，大部分是采用 BP神经网络及它的变化形式。

4.2 基于RBF神经网络的建模方法

径向基函数神经（Radial Basis Function neural）网络的网络结构分为三层：输入层由一些源点组成，将网络与外界联系起来；第二层是网络中仅有的一个隐层，它的作用是从输入空间到隐含层高维空间的非线性转换；输出层为线性层。对于RBF网络的训练，所需要确定的自由参数主要是其传递函数径向基函数的中心、宽度和输出单元的权值。而根据传递函数的自由参数确定方式不同，径向基函数网络又有着不同的训练学习策略，比如建立在插值理论基础之上的学习策略，结合正则化理论及核回归理论的学习策略。

蓄电池SOC估计是通过蓄电池的工作电流、电压和温度这三种便于测量的参数，估计蓄电池实时的荷电状态数值。对上述参数合理地选取，可以设计具有不同输入输出参数的多种 SOC估计模型。最为直接的方式是使用电压、电流和温度作为输入，SOC值作为输出，函数关系可以表述为：，这是标准模型。

5 建模方法比较

模糊系统对非线性映射有任意逼近能力，基于模糊理论的模糊辨识方法正广泛地被用于复杂系统的辨识与控制，因此亦有学者采用模糊理论进行蓄电池建模。

除以上常见方法外，还有一些不太常用的建模方法。主要有：回归分析建模方法、基于灰色理论的蓄电池建模方法、基于支持向量机方法的建模方法、键合图建模方法、基于Map模型的建模方法。由于建模方法较多，可以将两种建模方法结合使用，但是这些建模方法或者过于简单，或者过于理论化，应用以上建模方法作为大容量动力蓄电池建模的备选方案时应慎重。

基于电化学机理建立模型的难度大，并且模型计算与实际情况相差较大。基于电化学经验公式建模与基于等效电路建模，有一定的相近性，其关键问题在于公式中的众多参数如何确定。

基于神经网络的建模方法应用比较广泛。建立神经网络模型的关键是选择合理的网络结构、优化的算法以及大量合理的实验数据。其中网络结构可以通过程序的自动选择来实现，算法可以借鉴广泛应用的成熟算法。如果建立蓄电池充放电实验室，设计合理的充放电试验，获取大量有效数据，采用神经网络方法可以建立满足实际使用需求的蓄电池模型。

[1]Henry A. Catherino, Joseph F. Burgel, Andrew Rusek,etc. Modelling and simulation of lead-acid battery charging [J]. Power Sources, 1999, 17-20.

[2]马守军. 潜艇蓄电池建模策略分析[J]. 船电技术,2004(4):23~25.

[3]王治国. 铅酸蓄电池等效电路模型研究[J]. 装甲兵工程学院学报, 2003(3): 78~81.

[4]龚庆杰. 一种车用动力型蓄电池的建模仿真研究[J].蓄电池, 2005(2):76~79.

[5]赵建华. 现代潜艇铅酸蓄电池放电模型研究[J]. 武汉理工大学学报, 2006(4): 675~677.

[6]徐鲁杰. 潜艇用新型铅酸蓄电池万用放电模型研究[J]. 武汉理工大学学报, 2009(1): 177~179.