优化复合控制技术在有源电力滤波器中的应用
王雅 魏文新 张维
(1.中国船舶重工集团公司第七一二研究所,武汉430064;2.海军驻桂林地区军事代表室,广西 桂林 541002;3.海
军驻芜湖军事代表室,安徽芜湖 430033)
0 引言
电力电子装置和非线性负载的广泛应用,使得大量的无功电流和谐波电流注入电网,严重影响了电网和电气装置的安全运行和可靠使用[1]。APF与无源滤波器相比,可以动态的抑制谐波和无功电流,不易与系统发生谐振。近年来,单相APF逐渐成为研究热点[2]。
目前,对APF的研究主要集中在三相三线和三相四线并联型APF的指令电流的提取,控制性能的提高上[3,4],对单相有源电力滤波器的研究显得不足。对于APF的电流环而言,输入指令主要为快速变化的谐波信号,PI控制器的带宽有限,无法做到对这种多个频率正弦信号叠加的谐波电流的精确跟踪。基于内模原理的重复控制技术理论上可以实现对正弦指令信号的无静差跟踪[5],但基于工频周期的调节的重复控制的缺点是动态响应慢,如果设计不当,容易引起相邻频率谐波的相互干扰。因此对单相APF,本文提出了一种静止坐标系下的采用 PI控制和带前馈的重复控制相结合的电流复合控制策略。重复控制可以有效的增加系统的补偿精度,保证输出电流精确跟踪给定(负载谐波),前馈环节的引入可以有效的减小相邻频率间的相互干扰,有利于提高系统的稳定性,同时有利于增强系统的补偿精度,理论上也可以增加重复控制的动态性能。PI控制保证系统的动态性能,理论分析和实验结果均表明基于 PI和带前馈的重复控制并联运行的控制策略稳态精度高,动态响应快,补偿性能良好。
1 单相有源电力滤波器模型及其控制系统

图1 单相有源电力滤波器电路模型
单相并联型APF的电路模型如图1所示,Sa1,Sa2,Sb1,Sb2代表两个桥臂的开关管,L为 APF的输出电感,R代表输出电感内阻和每个桥臂的上下管互锁死区压降等效阻抗之和。Cdc代表直流母线上的滤波电容。
由图1可以建立静止坐标系下单相APF的数学模型如式(1)所示。


由式(1)可得单相 APF在静止坐标系下的数学模型框图如图2虚线框内所示,图2中电网电压是一个扰动量,考虑电网电压可能存在畸变以及给控制器提供一个稳态运行的工作点,加入电网电压前馈。
此时引入一个新的控制变量ur

将式(2)带入式(1)可得:

此时控制对象实际简化成一个一阶惯性环节,Sa1实际相当于APF桥臂中点的输出电压。
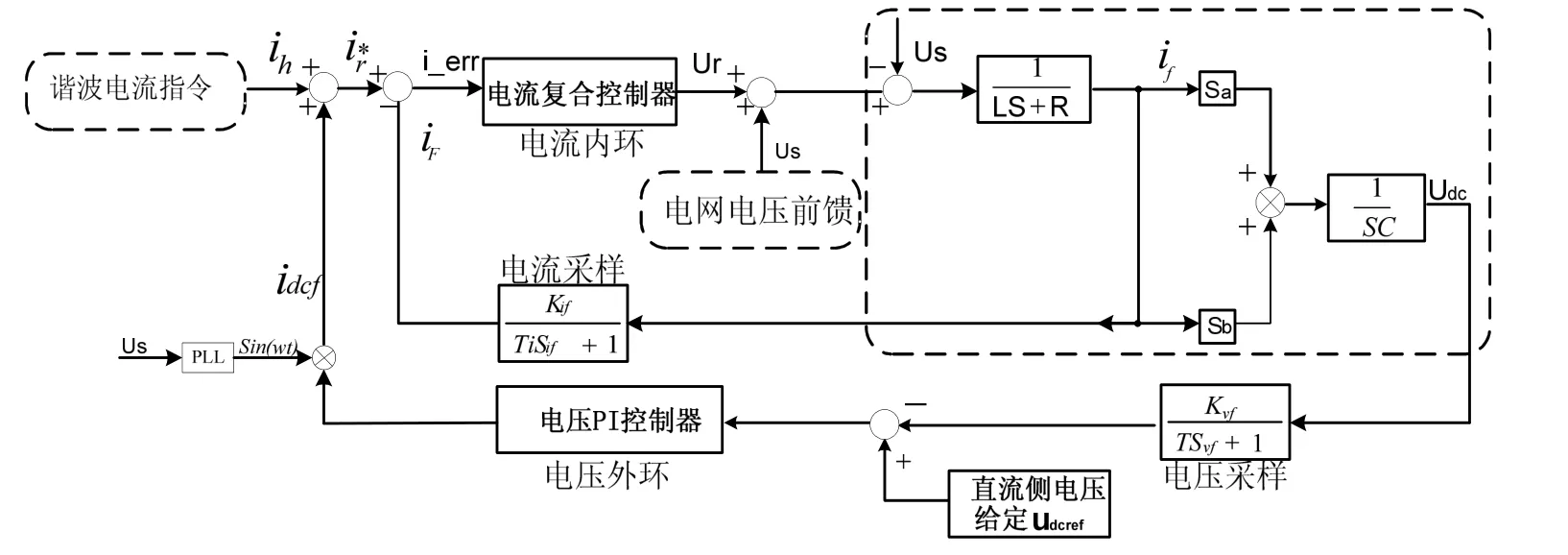
图2 单相APF控制框图
2 单相有源电力滤波器控制器参数设计
2.1 重复控制器的分析和设计
重复控制的等效结构图如图3所示,N为每周期采样次数。
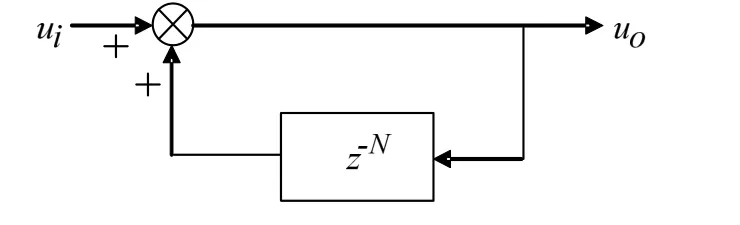
图3 嵌入式重复控制技术
重复信号发生器的离散形式是:

式(4)中N=T/Ts,T为基波周期,Ts为采样周期。由式(4)可以看出,这是一种类似“纯积分”环节的数学形式,这种“纯积分”的缺点在于引入了N个位于单位圆圆周上的开环极点,从而使开环系统呈现临界稳定状态,只要对象的建模略有偏差,或者对象参数稍微发生变化,闭环系统就极有可能失去稳定,对稳定性和鲁棒性不利。因此为了提高系统的稳定性,实际系统大多采用嵌入式的重复信号发生器,增加了滤波器 Q(z),Q(z)可以是一个低通滤波器,以减弱积分效果,如图4所示。

图4 改进的重复控制技术
其离散化的数学模型为:

一般取Q(z)为一个小于1的常数K,则由式(5)可知,嵌入式重复控制的谐振峰值为1/(1-K),在节点处的最小增益为1/(1+K)。在改进型重复控制器的基础上增加一个前馈环节,如图5所示,引入位于极点之间的零点,谐振峰值由原来的1/(1-K)变为(1+K)/(1-K),同时在节点处最小的增益由原来的1/(1+K)变为(1-K)/(1+K),可以获得更大的带宽,有利于增强系统的补偿精度,提高系统的稳定性。同时邻极点之间的最小增益减小,使得在同一时间内不同频率的谐波增强了选择性。
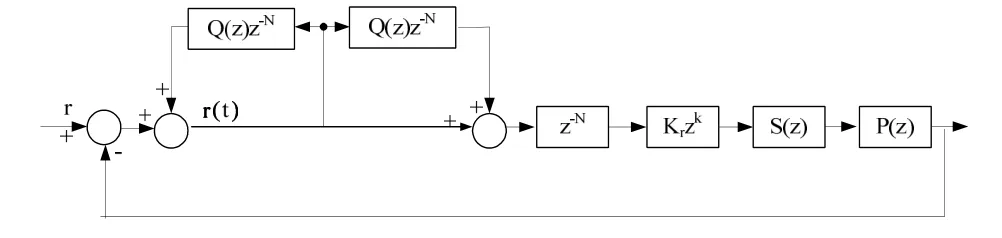
图5 带前馈的重复控制器
其输入输出关系为:
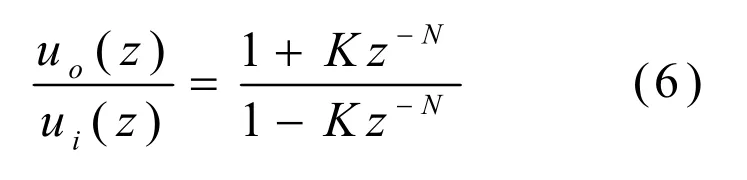
带前馈的嵌入式重复控制器结构如图 5所示,Q(z)是一个低通滤波器,本文中简单的取为一个小于 1的常数,与周期延迟环节 z-N串联构成重复控制器的内模部分。S(z)是针对控制对象P(z)而设置的补偿器。本文以工频周期正弦信号作为重复控制的内模进行设计,因此根据内模原理,只要以基波周期重复出现的信号,重复控制器理论上均可以做到对此稳态无静差的跟踪。
图5中,Q(z)不仅与控制系统的稳定性有关,而且与补偿精度有关,Q(z)的取值是以牺牲稳态精度来提高系统的稳定性的。本文中取Q(z)=0.95。上文中提到的,控制对象一阶惯性环节特性、系统采样、指令计算和滞后一拍的控制均会增大系统响应的延迟时间。因此用超前拍数环节来补偿数字控制的一拍延迟以及控制对象的相位滞后,本文通过估算和实验验证选取超前拍数为2,即超前环节为z2,选取合适的Kr来调节重复控制器的收敛速度,Kr不能取的太大,否则容易导致系统的不稳定。本文取Kr=0.5,此时补偿器S(z)设计为KrS(z)。
2.2 PI控制器的分析和设计
由上述分析可知,控制对象可以简化成一个一阶惯性环节,因此基于PI控制的电流闭环控制系统为一个典型的二阶系统,可以采用零极点对消的方式将此时的闭环传函简化成一阶模型,这种方法的核心思想就是使控制器的零点偏移到该系统在S平面的极点。
取比例常数Kp和积分常数Ki为

此时可以得到基于 PI控制的电流环闭环传递函数如式(5)所示。

式(8)中Tf为系统响应的延迟时间。由式(8)可知,系统延迟响应时间与比例常数Kp成反比,与输出电感L成正比,因此减小输出电感和增大比例常数有助于提高系统的补偿精度,但是控制对象一阶惯性特性决定了PI控制无法消除延迟,系统采样、指令计算和数字控制一拍滞后的特性使得电流响应的时间延迟变严重,因此增大比例常数、减小输出电感对输出电流的跟踪精度改进有限,而且可能引起其他问题,如导致系统不稳定,引起系统振荡等。
2.3 改进的复合控制策略分析
为了同时兼顾系统的动态特性和稳态性能,在单相有源电力滤波器控制系统中,将重复控制器与 PI调节器并联运行使用组成电流复合控制策略,如图6所示。
当系统稳态运行时,系统的跟踪误差小,重复控制占主导作用,PI控制器作用很小;当系统出现大的扰动时,重复控制器由于存在一个工频周期的延时,在扰动瞬间,一个工频周期内无法产生调节作用,而PI控制迅速调节,一个基波后重复控制器调节作用使跟踪误差减小,直至系统达到新的稳定运行状态。

图6 电流环复合控制器框图
3 实验结果
为了理论分析的正确性,在研制的22kVA单相并联型APF实验平台上进行验证,电路结构参数如表1所示。

表1 并联型APF实验系统电路结构参数
搭建的单相不控整流桥带 RL型负载作为谐波源,直流侧电感和电阻分别为8 mH和5.5 Ω。图7为非线性负载电流波形,即APF未投入工作时,系统侧电流波形,由频谱分析可以看出,畸变电流为奇数次谐波电流,其中3次谐波畸变率为14.8%,总谐波电流畸变率(THD)为20.4%。

图7 补偿前系统电流波形和频谱分析
电流内环单独采用 PI控制时的补偿效果如图8所示,可以看出,在固定点处的电流阶跃依旧很明显,3次谐波畸变率从补偿前的 14.8%降低到8.9%,THD由补偿前的20.4%降低到13.8%,可见PI的补偿效果有限,尚未达到谐波抑制的国家标准。
采用 PI控制和带前馈的重复控制并联运行的电流复合控制策略下,补偿效果如图9所示。3次谐波畸变率从14.8%降低到1.73%,THD下降至 3.6%,补偿精度得到显著提高,波形质量得到明显改善,达到了谐波抑制的国家标准。

图8 单独PI控制器时系统电流和电流频谱

图7 复合控制补偿时系统电流和电流频谱
4 结论
本文分析了PI控制器在单相APF中应用的局限性,为改善单相APF稳态时补偿精度,同时兼顾其动态响应特性,提出了PI控制器和带前馈的重复控制器相结合的电流复合控制策略,并从理论上分析了带前馈的重复控制的优势。实验结果表明改进的复合控制策略可以明显提高单相APF的补偿性能,达到了谐波抑制的国家标准。
[1]王兆安, 杨君, 刘进军.谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998
[2]T. Tanaka, E.Hiraki, K.Ueda, K.Sato, S.Fukuma. A Novel Detection method of active and reactive currents in single phase circuits using the correlation and cross-correlation coefficients and its applications[J]. IEEE transactions on power delivery, 2007, 4(22):2450-2456.
[3]李战鹰, 任震, 杨泽明. 有源滤波装置及其应用综述[J]. 电网技术, 2004, 28(12): 40-43.
[4]李江, 孙海顺, 程时杰等. 基于灰色系统理论的有源滤波器预测控制[J]. 中国电机工程学报, 2002,22(2): 6-10.
[5]Robert Griñó, Rafael Cardoner, Ramon Costa-Castelló,Enric Fossas. Digital repetitive control of a three-phase four-wire shunt active filter[J]. IEEE transactions on industrial electronics, 2007, 54(3):1495-1503.

