有源滤波器复合控制策略的研究
吕敬高
(海军驻湖南地区军事代表室,湖南湘潭411101)
0 引言
目前,滤除谐波主要采用无源滤波器和有源电力滤波器(APF)两种方式。APF与传统的无源滤波器相比,具有响应速度快、补偿效果好、能够实现动态连续实时补偿等特点[1~3]。因此,近年来,有源滤波器得到了迅速的发展。
现今对APF补偿电流的控制方法大多采用传统PI控制[4-5]。PI控制算法简单、可靠性高,被广泛应用于工业过程控制中。本文将广义积分控制器引入APF电流跟踪控制环节中。为了进一步改善传统广义积分控制器的动态性能,本文设计了一个模糊辅助调节器来动态调节广义积分控制器的各个控制参数,以同时获得较好的动态性能与稳态性能。并通过仿真与实验验证了此复合控制器性能。
1 APF的工作原理
图1显示了三相并联APF系统的主电路结构图。三相二极管整流桥作为非线性负载,一个电压源的逆变器被用作APF。
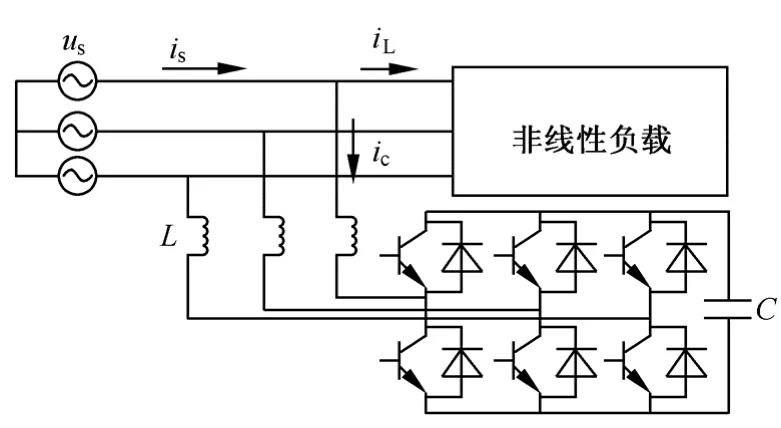
图1 三相APF系统结构图
从图1可以看出

因为并联型有源滤波器主要是用来补偿谐波电流的,而且现在主要的谐波污染是电流谐波,所以在本文中研究并联有源滤波器性能的过程中,均假设电源电压为理想的,即为单一频率的正弦波形,可表示为:

其非线性负载中含有基波电流 iLf和谐波电流iLh。基波电流iLf又包含有功和无功两部分,如式(3)所示。

式(5)表明,通过对 APF的合理控制,则三相电源只需提供负载的基波有功电流,从而达到补偿负载无功和消除谐波的目的。
并联型有源滤波器电流控制主要由两大部分组成,即指令电流运算和补偿电流发生部分,其中补偿电流发生部分又包括电流跟踪控制电路、驱动电路和主电路三部分。电流跟踪控制器的性能直接决定有源滤波器谐波补偿性能的好坏,如何设计一个好的电流控制器至关重要。
2 广义积分电流控制器
2.1 广义积分算法
如果 APF采用对电源电流直接闭环控制的电流跟踪策略,电流的参考信号是由多个频率的谐波叠加而成的,为了进行APF的无差调节,实现被控量对其给定参考值的无差跟踪,需要将多个不同频率谐波的广义积分器并联使用。事实上,根据工程实际的要求以及电网或者非线性负载的特征谐波次数,APF只需要着重治理有限的几次谐波。比如,谐波源为三相全控整流桥时,其特征谐波为6k±1次,APF一般只需要抵消5、7、11、13、17、19次谐波,电源电流就非常接近于基波正弦信号,所以控制器只要包含与这些谐波相对应的广义积分器,再加上比例调节器,如图2所示,APF就可以达到满意的电流跟踪性能。控制器传递函数如式(6)所示。

图2中,uc是逆变器电压参考,is是电源电流参考,is是电源电流。KP是比例系数,Kih等是广义积分器的系数,h表示谐波次数,ω1为基波角频率,e是电源电流参考值和实际值的误差,也即为ish。采用图2所示的电流控制器,可以有选择地对5、7、11、13、17、19次谐波进行补偿。
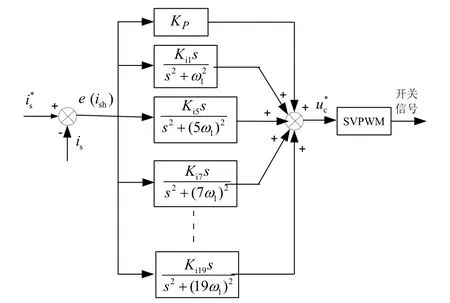
图2 APF广义积分电流控制器
2.2 广义积分控制算法的稳态无差特性分析
本小节将从闭环控制的角度,对广义积分迭代控制算法的稳态无差特性进行理论分析。
控制方式为:

GA的传递函数为:
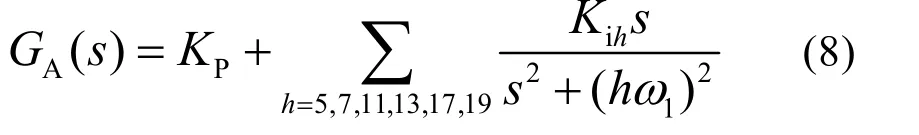
定义谐波抑制比参数为:

此谐波抑制比可以很好地体现谐波抑制特性,表征谐波衰减率,将式(8)代入,可以看出γ(s)含有6个零点s=hω1(h=15,7,11,17,19),因此有:

即Ish(hω1)=0。因此,流入电网的h次谐波电流为零。
可以看出,电源电流谐波不含有h倍基波频率的信号,即对这些频率的信号,广义积分控制器可以实现无差控制,能够保证随着时间的推移,APF的输出电流对参考电流的跟踪误差趋进于零,从而使电源电流也接近于理想的状态。
式(8)的波特图如图3所示,可以看出,指定次谐波都得到了有效地衰减。
3 复合控制器的设计
为了提高控制系统的鲁棒性和抗干扰性,本文将模糊控制理论引入到广义积分控制器中来,设计了一个带有自调整因子的辅助模糊控制器来根据系统的实际情况,实时地调整广义积分控制器的控制参数。
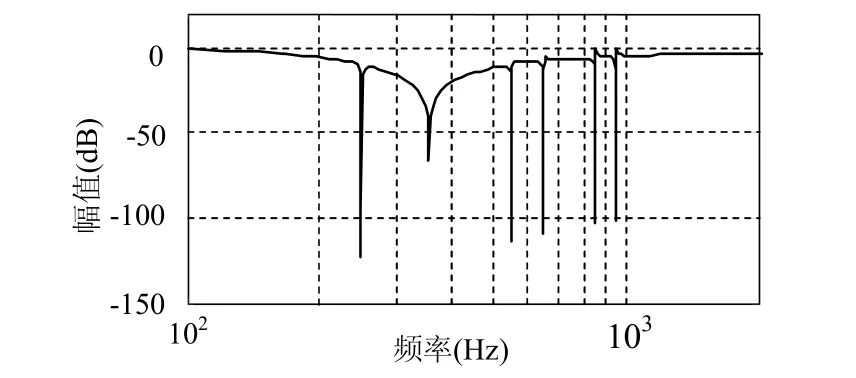
图3 电流谐波衰减率
在广义积分 PI控制器中,比例环节的作用是成比例地反映控制系统的偏差信号 e,偏差一旦产生,控制器立即产生控制作用,以减少偏差;如果比例控制参数Kp取值过大,会引起系统振荡,破坏系统动态性能。因此,当偏差e较大时,为提高系统响应速度,Kp取大值;当偏差较小时,防止超调过大产生振荡,Kp应减小;当偏差e很小时,为使系统尽快稳定,则Kp应继续减小。同时也应考虑误差变化率e˙的因素,当e和e˙同号时,输出向偏离稳定值的方向变化,此时应适当增大Kp;反之,适当减小Kp。
积分环节主要用于消除静差,提高系统的稳态精度。它对误差进行积分,对系统控制有一定的滞后作用,积分作用过强,会造成系统超调增大,甚至引起振荡。在常规PI控制器中,为防止积分饱和,常将积分环节分离出来,当误差减小至一定范围时,才加入积分环节。因此,当误差e较大时,为避免系统超调,Ki取零值;当误差e较小时,积分环节有效,随着误差e的减小而增大,以消除系统的稳态误差,提高控制精度。
基于以上思想,本文所设计的改进广义积分控制器的结构如图4所示,它由广义积分控制器和自调整模糊辅助控制器组成。使用自调整模糊辅助控制器主要是为了实现广义积分 PI控制器参数的在线实时整定,即根据系统的采样误差信息,将误差e和其导数˙输入模糊控制器,通过模糊决策,在广义积分PI参数预整定的基础上实时在线整定PI参数,以达到最佳控制效果。
所采用的模糊控制器为二维输入、二维输出控制器,根据不同的输入e、计算出输出ΔKi,从而实现广义积分PI控制器参数的调整,如下所示:


图4 基于模糊调整的广义积分控制策略
在模糊控制系统中,模糊控制器的性能对系统的影响很大,而模糊控制器的性能在很大程度上又取决于模糊控制规则的确定及可调整性。在这里设计了一种在全论域范围内带有自调整因子的模糊控制器,其通过引入一个可调的参数对控制规则进行调整,以便适应系统的复杂多变性。本文采用的带有自调整因子的 Kp模糊调整规则可以表示为:

式中, 0 ≤ α0≤ αs≤1为常数, α ∈[α0, αs]是自调整因子,N为量化等级常数, E*与分别为e和˙的模糊量,ε为预置的阀值,即当误差大于此阀值时,采用本文设计的调整策略对比例系数进行实时调整;而当误差小于此阀值时,不再调整比例系数,将其设置为预置值,以防止引起振荡。
本文设计的积分系数Ki的模糊调整规则如式(12)所示:

式(12)所示调整规则是基于上述基本调整原理得出的,即当误差非常大的时候,先不采用积分环节,防止过大的超调及振荡的发生;当误差减小到一定程度后,投入积分环节;当误差减小到较小阀值时,此时应加强积分环节作用,并且为了防止频繁调节带来的抖动,将积分变动值设定为一个固定的值ζ,以更好地提高稳态精度。
4 仿真与实验验证
为验证所设计的改进广义积分控制策略的有效性,利用 MATLAB进行了仿真研究,并与传统的PI控制进行了比较,主要从稳态精度与动态响应速度两个方面进行比较。仿真结果如图 5、图6所示,可以看出,在APF投入后,电网电流中的谐波分量得到了有效地补偿。当负载电流在0.2 s发生变化时,基于本文所设计的改进广义积分控制策略可以更好地、更为快速地跟踪负载电流的变化,其动态响应速度与稳态精度都比传统的PI控制器高。

图5 基于改进广义积分控制器的系统响应曲线

图6 基于传统PI控制器的系统响应曲线
为了进一步验证本文所提出的复合控制策略的正确性、有效性,本文在实验平台上面进行了实验研究。实验中谐波源为三相整流桥带阻感负载,实验波形采集用示波器为 Tektronix TDS 3032。实验结果如图7、图8所示。可以看出,在改进的广义积分控制策略下,APF可以很好地补偿谐波电流,并且可以在一个电网周期内快速地跟踪负载电流的变化,性能优于传统PI控制策略,与仿真结果相吻合。

图7 改进广义积分控制下APF投入前后的电源电流曲线

图8 传统PI控制下APF投入前后的电源电流曲线
5 结论
控制系统是 APF的关键环节,直接影响到APF的工作性能。APF的控制系统包括补偿电流跟踪控制和主电路直流侧电容电压控制。
对于电流跟踪控制,本章设计了基于模糊自调整的广义积分控制策略,通过模糊辅助调整器来动态调节广义积分控制器的各个控制参数,使此电流控制器可以同时获得较好的动态性能及稳态性能。
[1]王兆安, 杨君, 刘进军. 谐波抑制和无功功率补偿[M]. 北京: 机械工业出版社, 1998.
[2]EI-Habrouk M, Darwish M K, Mehta P. Active power filter: a review[J]. IEE Proceedings-Electrical., Power Application, 2000, 147(5): 403~413
[3]顾建军, 徐殿国, 刘汉奎等. 有源滤波技术现状及发展[J]. 电机与控制学报, 2003 , 7(2): 126~132.
[4]D.M. Brod, D.W. Novotny. Current Control of VSIPWM Inverters. IEEE Procs. of IAS.1984: 418~425.
[5]J. Dixon, S. Tepper, L. Moran. Practical Evaluation of Different Modulation Techniques for Current-Controlled Voltage Source Inverters. IEE procs. Electr.Power Appl. 1996, 143(4): 301~306.

