基于FPGA的无人机MLS中频接收机研究与实现
王 伟, 张 斌, 吴 松
(空军工程大学电讯工程学院,西安 710077)
0 引言
大型无人机自主着陆问题是影响无人机飞行安全和出勤率的重要因素。国外无人机自主着陆多采用基于GPS的组合导航方式。国内无人机自动起降系统功能和性能还不能完全满足要求,相关标准尚未确立。微波着陆系统(MLS)是目前国内机场配备的精度最高的飞机进近着陆系统,其特点是信号覆盖空间大,精度高,受场地环境影响小,所提供的进近方式更加灵活[1]。采用MLS作为无人机的自主导航系统,可以充分利用现有地面资源,在飞机上安装一部接收机,提供精密的制导信息,同时摆脱了GPS受制于人的缺陷。因此,研究MLS信号的高精度解调具有十分重要的意义。
MLS信号中的数字信息采用2DPSK调制方式,采用相干解调精度较高,对MLS信号进行相干接收时,要求本地载波与接收信号载波同频同相,载波同步的方法包括直接法和插入导频法,其中插入导频法要求输入信号含有载频信息,此处并不适用。直接法包括Costas环和平方环[2],平方环法需要倍频,频率较高时在工程上难以实现。Costas环是一种闭环自适应系统,能够高速高精度地完成载波同步和2DPSK解调,传统的模拟Costas环因存在同相支路与正交支路的不平衡性从而使环路的性能受到一定的影响,且模拟电路还存在直流零点漂移、难以调试等缺点,采用全数字的实现方式则可有效地避免这些问题[3]。另外,采用数字解调方式还具有体积小、重量轻、功耗低,调试简单等优点。
MLS的测角是基于时基扫描波束技术,通过测量“往返”扫描脉冲的时间间隔完成测角功能,因此,需要对MLS信号进行AM解调,得到扫描脉冲的包络,AM解调的精度直接影响着测角的精度。应用CORDIC算法设计Costas环的鉴相器和AM解调关键模块,这样,利用Costas环的部分电路就可以实现高精度数字正交AM解调。
1 MLS信号格式
MLS信号格式采用时分多路复用体制,方位制导、仰角制导和数据字信号工作在同一频率,各自占有一定的发射时隙[4]。方位和仰角信号的基本格式是前导码加扇区信号加扫描信号,数据字信号的基本格式是前导码加数字信息。前导码信号、扇区信号和数字信息为2DPSK调制信号,调制速率为15625 Hz,扫描信号为AM信号。前导码包括3部分:载波捕获段、基准时间码和功能识别码。载波捕获段为832 μs的未加调制载波,在此期间完成载波同步;基准时间码为5位巴克码,作用是产生时间基准;功能识别码的作用是区分接收信号的功能(发射的是方位信号、仰角信号还是数据字)。
2 MLS信号载波同步及AM解调原理
MLS信号工作在C波段(5031~5091 MHz),经天线接收后无法直接进行处理,在射频电路中经过两次下变频得到65 MHz中频信号,然后进行数字带通采样,根据带通采样定理,采样速率确定为8 MHz,采样后将中心频率为1 MHz的信号滤出,其携带有MLS信号的完整信息。
传统的Costas环只有一路反馈,同时调整本地频率和相位,捕获带较窄,相位抖动幅度大,对环路进行改进,增加鉴频电路,设计两路反馈,分别调整本地频率和相位,捕获带较宽,相位抖动幅度小。
AM解调基于数字正交解调原理,具有较强的抗载频失配能力,即允许本地载波与信号载波之间有一定的频差和相差。Costas环及AM解调的综合实现框图如图1所示。

图1 Costas环实现载波同步及AM解调原理Fig.1 Principle of carrier synchronizer based on Costas and AM demodulation
设经过A/D采样后,得到的2DPSK调制信号和AM信号分别为
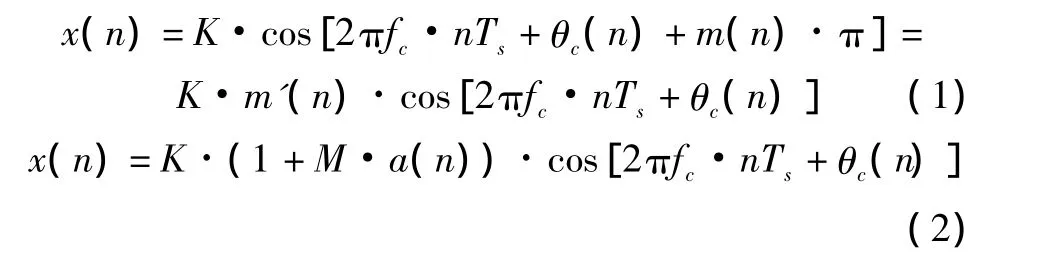
其中:m(n)为携带的数字基带信息,当m(n)=0时,m'(n)=1,当m(n)=1时,m'(n)=-1;K为输入信号的幅值;fc为经过A/D后的载频;θc(n)为瞬时相位;Ts为信号采样周期;1+M·a(n)为信号包络。
NCO输出两路正交信号为
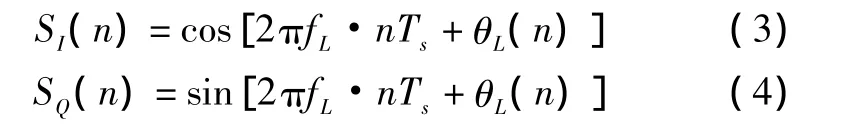
其中:fL为本地载频;Ts为采样周期;θL(n)为本地瞬时相位。
2DPSK调制信号经过数字混频和低通滤波器滤除高频分量后得到

在鉴相器中,根据式(5)和式(6)求反正切得到瞬时相位差2π(fL-fc)·nTs+θL(n)-θc(n),对相位差求一阶导数可以得到瞬时频率增量2π(fL-fc)·Ts,瞬时频率增量经过鉴频环路滤波器后调整NCO的频率,在完成频率锁定即瞬时频率增量为0后,瞬时相位增量经过鉴相环路滤波器后调整NCO的相位,完成相位锁定即瞬时相位差为0,此时将同相分量I(n)和正交分量Q(n)相加后可得到输出信号为
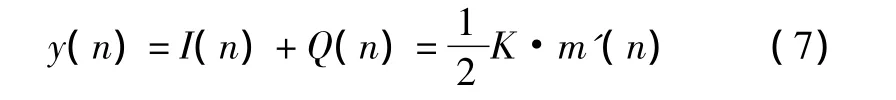
对y(n)进行相对码到绝对码的转换就得到数字基带信息。从整个解调过程可以看出,2DPSK解调实质上是Costas环锁相过程。因此,只要在832 μs内完成数字锁相,就可以准确地得到MLS地面设备发出的2DPSK基带信号。
根据MLS信号格式,实现载波同步后,进行基准时间码同步,功能码识别,如为数据字信号,则继续进行2DPSK解调,如为角度制导信号,则进行AM解调。AM信号经过相同过程得到I(n)和Q(n)。
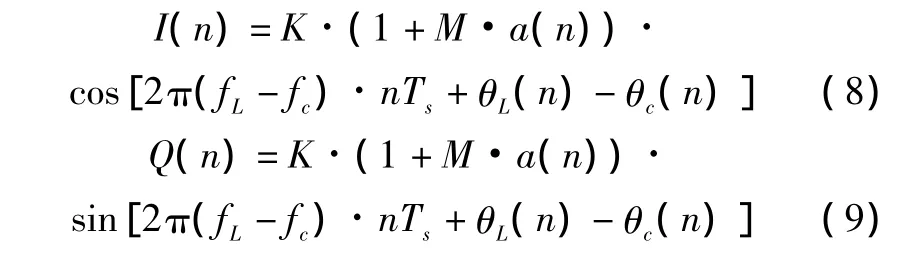
计算I(n)和Q(n)的平方和再开方就得到了信号的包络。
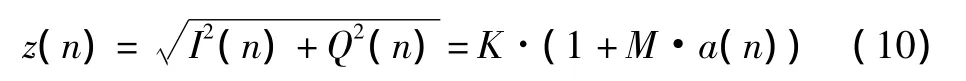
从推导过程可以看出,当接收信号载波与本地载波不同步时,AM解调精度不变。
3CORDIC算法
CORDIC算法可以通过简单的加法移位操作迭代计算 sin θ,cos θ,arctan θ等函数,避免了使用泰勒级数展开式计算所需的复杂乘法运算,特别适合于FPGA实现[5]。推广的CORDIC算法适用于圆周坐标、线性坐标和双曲线坐标,每种坐标系又分为向量模式和旋转模式,统一迭代方程如下。
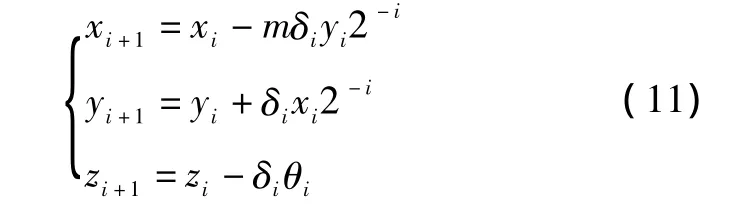
其中
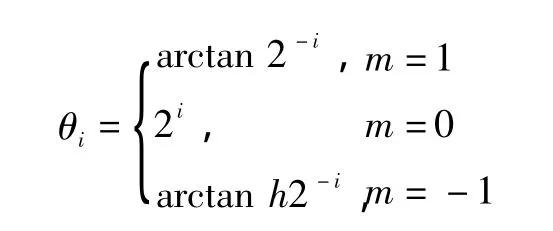
式中:m代表坐标系,δi代表旋转方向,θi代表旋转的角度,根据m和δi取值的不同,CORDIC算法可经过不同的设置实现不同的数学运算。
3.1 基于CORDIC算法的NCO设计
NCO的作用是产生正交的正弦和余弦样本,传统做法是采用查表法(LUT),即事先根据各个正/余弦波相位计算好相位的正/余弦值,并按相位角度作为地址在存储器中对其进行寻址,构成一个幅度/相位转换电路(即波形存储器),通过该转换电路进行查表获得正/余弦信号样本。为了提高数控振荡器的频率分辨率,往往需要扩大波形存储器的容量,占用大量资源。为了避免这一问题,考虑利用算法实时产生正/余弦样本,CORDIC算法正好满足这一需求。
应用CORDIC算法圆周旋转模式产生正余弦信号[6],令 m=1,则 θi=arctan 2-i,给定初值,x0=K1,y0=0,z0= φ,其中旋转方向由zi决定,若zi<0,则 δi=+1;若zi>0,则 δi=-1,经过n次迭代最终使zi趋于0。迭代的最终结果为
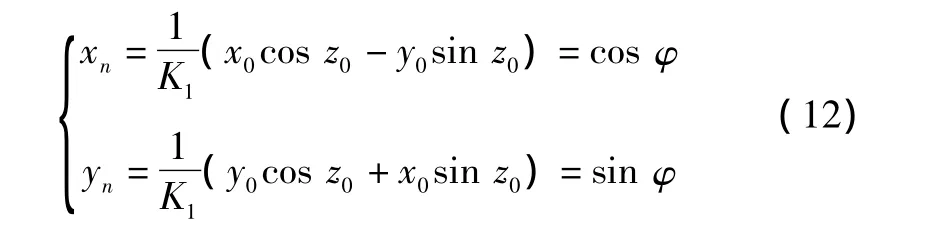
数控振荡器(NCO)的总体实现框图如图2所示,主要由频率调整累加器、相位累加器、相位加法器和CORDIC算法计算正余弦模块构成。
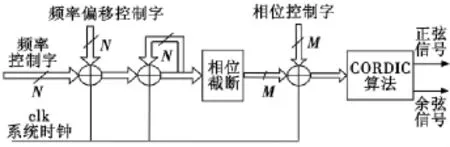
图2 数控振荡器(NCO)结构框图Fig.2 Block diagram of NCO
在系统时钟的控制下,频率偏移控制字不断调整频率控制字,对N位频率控制字进行累加,截取输出值的高M位与相位控制字相加,这样,每来一个时钟得到一个相位,用CORDIC算法计算该相位的正余弦值。当同步以后,维持频率控制字和相位控制字不变,NCO输出与接收信号同频同相的载波信号。
3.2 基于CORDIC算法的鉴相鉴频器和AM解调关键模块设计
数字鉴相器作为载波跟踪环路的核心部分,其精度和鉴相范围直接影响接收机的性能,数字鉴相的方法主要有4种:I·Q型、sign(I)·Q型、Q/I型、arctan(Q/I)型,其中基于反正切的相位误差检测最为精确,相比其他鉴相方法能够相对降低环路抖动[7],因此,采用arctan(Q/I)型鉴相器。传统的实现反正切方法是首先对同相支路(Q路)和(I路)做除法,然后根据反正切查找表找到其对应反正切值,缺点是除法硬件实现困难,查找表占用资源多。利用CORDIC算法可以解决这些问题。
从AM解调原理可以看出,重难点在于计算同相支路和正交支路的平方和再开方,计算平方和可以用两个乘法器和一个加法器实现,传统的开平方计算算法主要有实函数近似法、牛顿迭代法、冗余算法等,这些算法从根本上讲是使用了查表法或多项式展开近似,它们的速度和精度难以满足实用要求,硬件实现也非常困难,利用CORDIC算法计算平方和再开方,省去了乘法器和加法器,只有加法和移位,易于工程实现。
应用 CORDIC 算法圆周矢量模式[8],令 m=1,则θi=arctan 2-i,给定初值,x0=I(n),y0=Q(n),z0=0,旋转方向由 yi决定,若 yi<0,则 δi=+1,若 yi>0,则δi=-1,经过n次迭代最终使yi趋于0。迭代的最终结果为
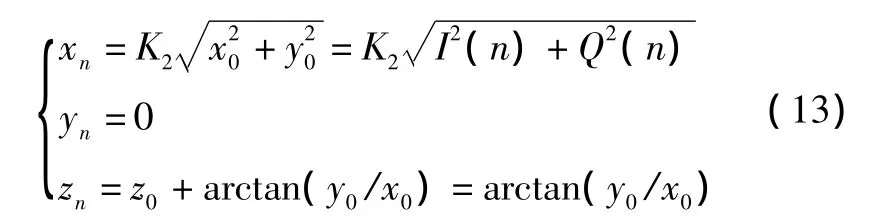
模拟域相位函数和模拟角频率函数之间关系为
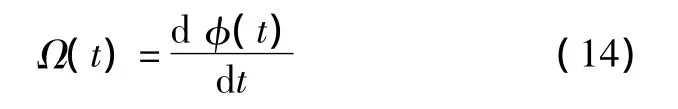
可以得到数字域的相位函数φ(n)和频率函数f(n)之间的关系为

其中,Ts为采样周期。考虑到数字域的数字频率ω(n)=f(n)·Ts,所以式(15)可以转化为

式(16)表明数字域频率和相位的关系是简单的一阶差分关系,所以只要利用CORDIC算法得到的瞬时相位差进行一阶差分就可以得到瞬时频差。
当检测到有输入信号时,鉴频环路滤波器开始工作,瞬时频差经过鉴频环路滤波器后作为频率偏移控制字不断调整NCO的频率控制字,直至完成频率同步,鉴频环路滤波器停止工作,鉴相环路滤波器开始工作,瞬时相差经过鉴相环路滤波器作为相位控制字不断调整NCO的相位,直至完成相位同步。
4 FPGA实现及信号分析
根据以上设计理论,在QuartusII8.0设计平台上用VHDL语言编程实现。CORDIC算法的实现方式有两种:基于状态机结构和基于流水线结构。状态机结构缺点是计算速度慢,流水线结构虽然占用资源相对较多,但对于现有FPGA芯片资源来说并不是问题,且运算速度快,可以实现高速实时处理,流水线单步迭代结构如图3所示。

图3 CORDIC流水线单步迭代结构Fig.3 Single step interation structure of CORDIC pipeline implementation
由于CORDIC算法旋转的角度范围为-99.9°~99.9°,不能达到 NCO 和鉴相器角度范围 -180°~180°的要求。因此,需要在初次迭代前增加一个特定的“起始”步骤来扩大角度覆盖范围,根据三角函数的对称性,如果输入的数处于第一、四象限,则第一步不需要旋转,如果处于第二、三象限,则需旋转+180°或-180°。NCO采用8级迭代加1级初始角度旋转运算,仿真结果如图4所示,鉴相器和AM解调关键模块采用9级迭代加1级初始角度旋转运算,仿真结果如表1所示。
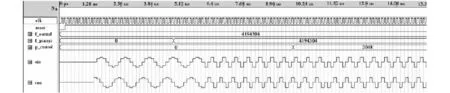
图4 NCO仿真结果Fig.4 Simulation of NCO

表1 鉴相器和AM解调关键模块仿真结果Table 1 Simulation of phase detector and key module of AM demodulation
在NCO中,采样频率fs=8 MHz,载频fL=1MHz,频率控制字位数N为25位,相位控制字位数M为12位,频率控制字为f_con=2N·fL/fs=4194304,输出正余弦样本位数为10位,从图中可以看出,频率偏移控制字和相位控制字可以灵活调整本地载波的频率和相位。
鉴相器和AM解调关键模块中,输入为10位,输出相位为12位,输出幅度为18位,其中8位表示小数,从表中可以看出,鉴相的误差在0.3°以内,AM解调的误差在0.1 mV以内。
根据CORDIC算法的原理和实现过程,如要求提高精度,可通过适当增加迭代次数和处理器字长,但这会降低运算速度,所以必须在这两者之间进行权衡。
当初始频差为20 kHz、初始相差为90°、信噪比为10 dB时,将在QuartusII8.0中仿真的结果保存为.tbl格式数据文件,用Matlab软件读取.tbl文件进行波形显示[11]。图5给出了改进Costas环与传统Costas环相位抖动的比较,从图中可以看出,改进Costas环相位抖动误差在2°左右,相对传统Costas环的4°误差有了很大提高,精度提高的代价是捕获时间变长,但只要满足832 μs的指标要求即可。另外,改进Costas环的另一优点是捕获带宽,可以达到±100 kHz,图6给出了频差为100 kHz,信噪比为10 dB时由改进Costas环解调出的数字基带信息为111010010100,其中前5位为巴克码,后7位为仰角功能识别码,完全符合要求。

图5 频偏20 kHz、相差-90°、信噪比10 dB时的相位抖动Fig.5 Simulation of phase jitter when frequency difference is 20kHz,phase difference is-90°and SNR is 10 dB
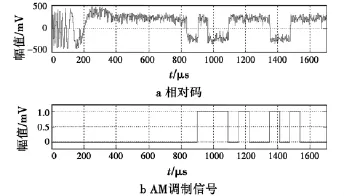
图6 2DPSK信号解调仿真结果Fig.6 Simulation of 2DPSK demodulation
图7给出了频差为100 kHz,信噪比为10 dB时的AM解调仿真结果,可以看出,较好地完成了MLS扫描信号的包络解调。

图7 AM解调仿真结果Fig.7 Simulation of AM demodulation
5 结束语
对Costas环进行了改进,捕获带较宽,相位抖动幅度小。数控振荡器、鉴相器和AM解调关键模块采用CORDIC算法设计,易于FPGA实现,利用同一电路完成MLS信号的2DPSK解调和AM解调,仿真结果表明,精度高、速度快、具有较高的工程应用价值。
[1]弋沛琦,高瑞乾,刘石源.飞机着陆系统的现状与发展[J].海军航空工程学院学报,2005,20(4):461-464.
[2]张欣.扩频通信数字基带信号处理算法及其VLSI实现[M].北京:科学出版社,2004.
[3]林海都,高强.基于FPGA的全数字Costas环的设计与实现[J].电子技术应用,2007,33(10):34-36.
[4]周其焕,魏雄志,崔红跃.微波着陆系统[M].北京:国防工业出版社,1992.
[5]骆艳卜,张会生,张斌.一种CORDIC算法的FPGA实现[J].计算机仿真,2009,26(9):305-307.
[6]郭立浩,段哲民,白森.采用CORDIC算法的直接数字频率合成器的设计[J].电光与控制,2006,13(5):77-79.
[7]王渊,黄颖.基于反正切相位检测的Costas环分析及FPGA 实现[J].通信技术,2010,43(8):124-126.
[8]余建宇,罗丁利,陈矛.基于CORDIC算法的数字鉴频方法及其在FPGA中的实现[J].火控雷达技术,2007,36(3):72-77.
[9]胡海华,杨芳,时华杰.基于CORDIC算法的AM基带解调方法[J].数据通信,2010(3):38-41.
[10]许建华,刘美娟,张超.基于CORDIC算法的数字中频检波技术研究[J].中国电子科学研究院学报,2007,2(5):531-535.
[11]王旭东,潘广桢.MATLAB及其在FPGA中的应用[M].北京:国防工业出版社,2006.

