基于加速度计的光电跟踪系统等效复合控制

杜 杰， 陈 娟， 郭 劲， 王威立

(1.中国科学院长春光学精密机械与物理研究所光电对抗部，长春 130022;2.中国科学院研究生院，北京 100039;3.长春工业大学电气与电子工程学院，长春 130012)

0 引言

目前提高光电伺服系统跟踪精度的方法很多，包括动态高型控制方法、共轴跟踪技术、速度滞后补偿技术、复合控制以及自适应控制、模糊控制、专家控制、神经网络控制等［1－2］。动态高型控制方法通过增加积分环节以提高系统的无静差度，但增加积分环节会影响甚至破坏系统的稳定性，而且缺乏普遍性［3］。文献［4］进行了动态Ⅲ型系统跟踪能力的Matlab仿真。共轴跟踪是计算机技术与复合控制相结合产生的一种新思想。共轴跟踪的关键是预测滤波技术，预测目标的位置、速度和加速度等运动状态［5－7］。速度滞后补偿技术是通过对速度的滞后进行补偿进而提高伺服跟踪精度［8］。复合控制系统是在系统的反馈控制回路中加入前馈控制通路，组成一个前馈控制和反馈控制相结合的系统，相应的控制方法称为复合控制。复合控制较好地解决了精度和稳定性之间的矛盾问题。等效复合控制为复合控制的另一种实现，现有的等效复合控制方法中速度信息是通过编码器测得的位置信号微分得到的［1，7］。本文利用加速度计直接测得加速度的信息再通过积分得到速度，并且用以实现等效复合控制。通过实验对比，得出基于加速度计信息的等效复合控制能够将光电跟踪系统的跟踪精度提高到原来的6.67倍，有力地说明了加速度计可以作为等效复合控制的传感器，并且将系统的精度提高。

1 等效复合控制

光电跟踪系统是一种跟踪测量系统，当目标进入电视视场后，系统能够自动捕获并且跟踪目标［5］。光电跟踪伺服控制系统是由方位和俯仰的两个控制系统组成，方位和俯仰两套相互独立又相互配合的伺服系统，采用直流力矩电机驱动，速度、位置回路双闭环控制方式。伺服控制系统组成如图1所示。

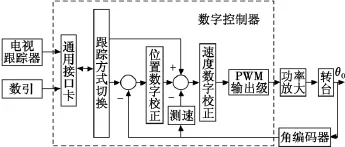
图1 伺服控制系统组成图Fig.1 Composition of servo control system

复合控制包括前馈和反馈通道，其误差全补偿条件是前馈通道的传递函数为被控对象传递函数的倒数［9］，复合控制系统的特点是在不影响原来反馈系统绝对稳定条件下，通过前馈控制提高系统的跟踪精度［10］。图2为按输入补偿的复合控制系统框图。

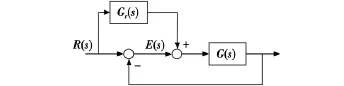
图2 按输入补偿的复合控制系统Fig.2 Compound control system with input compensation

由图2可知，系统的输出量为

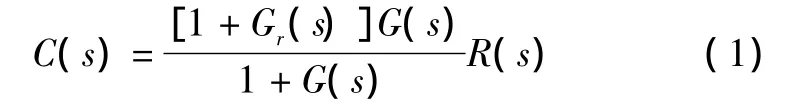
如果选择前馈补偿装置的传递函数

则式(1)变为

式(2)成立的条件下，系统的输出量在任何时刻都可以完全无误差地复现输入量，具有理想的时间响应特性［11］。复合控制之所以能使系统误差等于零，是利用双通道使正、反作用相消的原理。图2中，R(s)直接作用于系统的输入端，同时，通过Gr(s)G(s)再反馈回来的反作用于系统的输入端，由式(2)，Gr(s)G(s)=1，使得C(s)=R(s)，输入端的正反作用相互抵消，这说明系统误差E(s)对输入信号具有不变性。粗略地说，这种利用双通道(或多通道)使外作用正负抵消从而保证系统某些物理量不受影响的原理，称为不变性原理［12］。

当光电跟踪系统无法测得目标特性，即无法直接得到目标的速度信息时，复合控制无法实现，因此等效复合控制是复合控制(又称前馈控制)的另一实现。通过编码器与目标的脱靶量合成目标位置，再对此位置微分滤波后得到的速度来构成等效复合控制，因为编码器与电视的采样时间不同，所以干扰很大，并没有达到良好的实现效果。通过编码器一次微分和两次微分得到的跟踪系统速度和加速度信息，并以此实现的等效复合控制，简单实用，能够提高系统的跟踪精度。但经过微分后的加速度信息干扰很大，需要进行低通滤波［1］。通过加速度计直接测得的加速度再积分得到速度来等效目标输入信号的速度。等效复合控制结构如图3所示。

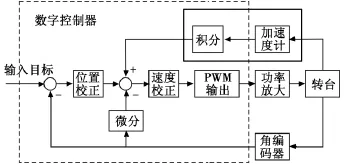
图3 等效复合控制框图Fig.3 The block diagram of equivalent compount control

图3中，实线框中的加速度计和积分模块为加速度信号采集系统，采集系统主要完成加速度计信号的采集、处理。

2 加速度计提供等效复合控制信息源

实验测量用加速度计为CJ41A－2E压电式角加速度传感器，测量范围－100～+100(°)/s2，分辨率≤0.02(°)/s2，电压输出范围为 －8 ～ +8 V(DC)，频率响应0～50 Hz。

2.1 加速度计信号的采集

加速度计信号的采集硬件框图如图4所示。

图4 加速度信号采样的硬件框图Fig.4 The hardware diagram of the acceleration signal sampling

其中A/D芯片为16位的 AD974，采用双极性－10～10 V量程。控制器采用AVR公司的ATmega16单片机。

加速度计信号的采集的软件实现过程为:AD974的读取是通过ATMEGA16的8位SPI通信完成的，由于AD974每次转换后的数字信号是16位，所以需要在一次转换完成后连续读取两次SPI的移位寄存器SPDR里的值。由于由16位的AD转换直接采集出的数据干扰很大，所以实验中采取了低通数字滤波器来对采集出的数据进行滤波。程序流程如图5所示。

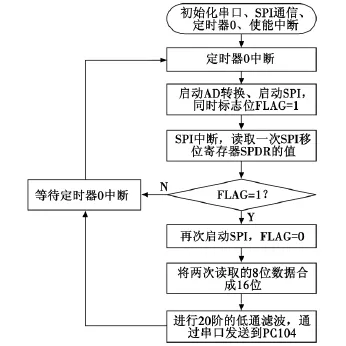
图5 程序流程图Fig.5 The flow chart of the program

2.2 速度的获取

通过对加速度计得到加速度，积分后获得速度，用于等效复合控制。

当方位系统以最大角速度20.4(°)/s，最大角加速度12.4(°)/s2运动时，实际测得的加速度信号与输入的加速度对比曲线如图6所示。

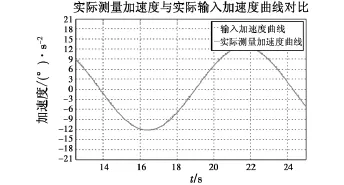
图6 实际测得加速度与输入加速度对比Fig.6 Curves of measured acceleraton and input acceleration

转台稳定后实际的加速度曲线对比如图6所示，从图中可以看出，实际测得的加速度曲线与输入加速度曲线基本吻合，但是伴随着一定的随机误差，通过计算实际测得加速度最大的随机误差为0.5(°)/s2。

因为要对加速度信号进行积分，所以设加速度函数为x(t)，则速度函数y(t)与其关系如式(4)所示，x(t)拉氏变换函数为x(s)，y(t)拉氏变换为y(s)，则将式(4)进行拉氏变换后如式(5)所示。

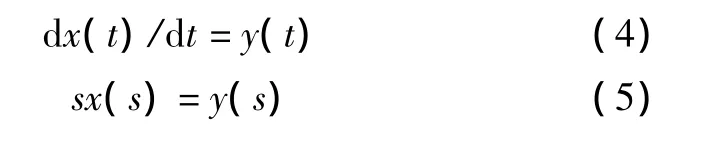
加速度积分的模型如图7所示。

图7 积分模型Fig.7 The integral model

图中:x(s)为加速度的s域函数;y(s)为积分后的速度s域函数。

由1/S 的 Z 变换为1/1 －z－1［10］可以将式(1)转换到Z域，如式(6)所示。

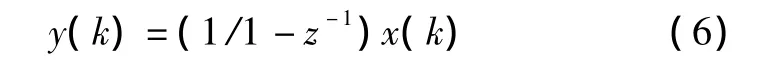
由式(6)可以进一步得到加速度x(k)和积分后的速度y(k)的差分方程关系，如式(7)所示。

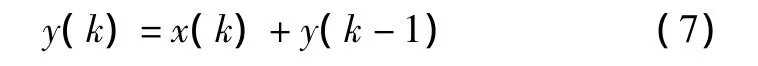
式中:y(k)为速度的第k个采样点;y(k－1)为速度的第k－1个采样点;x(k)为加速度的第k个采样点。通过这个差分方程，就可以在PC104中实现积分运算。

积分会对误差积累，随着时间的推移积分出的误差就会越来越明显。因此，实际测得的加速度零点可能偏上或者偏下，这样就会导致积分出的速度整体以一定的斜率向上或者向下漂移，需要对计算出的速度进行误差补偿。本实验采用的积分补偿公式如式(8)所示。

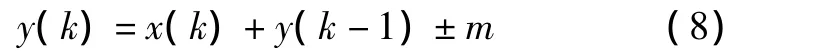
即在式(7)的右边加上或者减去一个常量进行补偿，式(8)中，m的具体大小要通过实验测试得到。补偿后的曲线与输入的信号的速度进行比较，如图8所示。

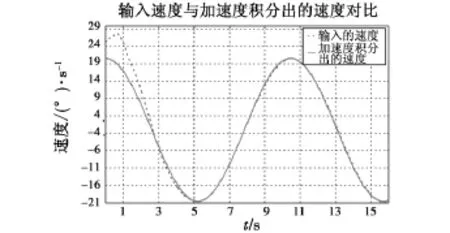
图8 补偿后的速度曲线与输入的速度对比Fig.8 Curves of compensated speed and input speed

经过补偿后的速度曲线，在积分的初期即第3000个采样点之前，由于加速度从0迅速上升导致积分出的速度从 0(°)/s 突变到 24.2(°)/s，而且与输入速度信号相差很大。3000个采样点后积分出的速度逐渐稳定并且逼近输入的速度。积分后的速度信号很平滑，通过图8的对比可以得出，积分后的速度曲线滞后输入速度曲线0.025 s，随机误差很小，稳定后的最大的随机误差为0.07(°)/s。

3 等效复合控制实验与分析

实验基于光电经纬仪的方位轴，方位轴输入θ(t)=34°sin(0.6t)的正弦信号，根据等效正弦公式［13］，可以求出最大角加速度为 12.4(°)/s2，角速度为 20.4(°)/s。有无前馈控制的系统误差曲线对比如图9所示。

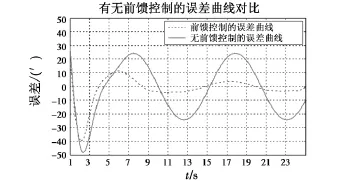
图9 有无前馈控制的误差曲线对比Fig.9 Curves of tracking error with and without feed-forward control signal

为防止系统没有进入稳态前复合控制信号对系统影响过大，所以前馈速度信号的增益是随着采样时间的增加逐渐增大的，因而在系统刚开始运行时，尽管加入了前馈控制信号，但是由于增益不大，误差减小很少。从图9可以得出加入前馈控制后的系统响应时间变短，系统提前1000个采样点即1.25 s进入稳态，稳态最大随机误差为0.4146'，稳态最大误差为3.628'。没有前馈控制的系统稳态最大随机误差为0.11'，系统稳态最大误差为24.2'。可见，加入前馈控制的系统稳态随机误差增加为原来的4倍，但是最大稳态误差明显减小，精度是没有加入前馈控制的跟踪系统的6.67倍。

4 结论

通过积分得到的速度非常平滑，当系统稳定运行时与输入目标的速度信号相差不大，可以作为等效复合控制信号。通过实验对比得出加入等效复合控制的光电跟踪系统使稳态误差明显地减小，精度提高为没有加入等效复合控制光电跟踪系统的6.67倍，说明加速度计可以作为等效复合控制的传感器，并且提高光电跟踪系统的跟踪精度。编码器微分后的速度和加速度计积分后的速度分别作为前馈控制信号的实验对比将作为下一阶段实验重点，两者对光电跟踪伺服系统的跟踪精度的影响也需进一步的研究。

［1］王建立.光电经纬仪电视跟踪、捕获快速运动目标技术的研究［D］.长春:长春光学精密机械与物理研究所，2003.

［2］章卫国，卢京潮，吴方向.先进控制与方法导论［M］.西安:西北工业大学出版社，2000.

［3］BRADLEY L M，CORRIVEAU J P，TINDAL N E.Launch area theodolite system［C］//Acquisition，Tracking and Pointing XII(C).Orlando，Florida，USA:SPIE，1991:48-60.

［4］邢启江，董二宝，陈娟，等.光电经纬仪伺服系统动态高型控制［J］.电光与控制，2007，14(3):140-143.

［5］马佳光.捕获跟踪与瞄准系统的基本技术问题［J］.光学工程，1989，81(3):1-42.

［6］ULICH B L.Overview of acquisition，tracking，and pointing system technologies［C］//SPIE，1988，887:40-63.

［7］韩晓泉.模糊控制在光电跟踪伺服系统中的应用研究［D］.北京:中国科学院研究生院，2004.

［8］王毅，魏忠和.补偿伺服系统速度误差和加速度误差的方法［J］.光学精密机械，1973，38(2):82-84.

［9］陈娟.光电跟踪伺服系统先进控制策略概述［J］.光机电信息，2007(12):56-61.

［10］孙丽娜，宋悦明，戴明.采用复合控制提高机载光电平台的数引跟踪精度［J］.光学精密工程，2008，16(2):265-269.

［11］胡寿松.自动控制原理［M］.4版.北京:北京科学出版社，2001.

［12］曾乐生，施妙和.随动系统［M］.北京:北京工业学院出版社，1988.

［13］动态高型控制方法在光电经纬仪跟踪伺服系统中的应用［D］.北京:中国科学院研究生院，2004.