基于最小二乘支持向量机的岩土本构关系曲线拟合

杨 春，孙佳佳

(河南理工大学土木工程学院，河南焦作454003)

最小二乘支持向量机和支持向量机原理一样都是根据统计学理论提出的一种新的通用学习方法［1］，它是以统计学理论的VC维(Vapnik Chervonenks Dimension)理论和结构风险最小原理(Structural Risk Minimization Inductive Principle)为基础的，其思路是通过用内积函数定义的非线性变换将输入空间变换到一个高维空间，在这个高维空间中寻找输入变量和输出变量之间的一种非线性关系。最小二乘支持向量机继承了支持向量机能较好地解决小样本、非线性、高维数和局部极小点等项优点。最小二乘支持向量［2］是对支持向量机的一种改进，最小二乘支持向量机有着自身的优势:(1)用等式约束代替支持向量机中的不等式约束;(2)将支持向量机中求解二次规划问题转化为求解线性方程组。(3)减少了运算量，提高了运算速度。

最小二乘支持向量机已成为学者们研究的热点，目前已经将其成功地应用于模式识别、函数拟合、时间序列预测和岩土力学与工程等方面。

1 最小二乘支持向量机的原理

最小二乘支持向量机的的结构构成［3］如图1所示。在特征空间中，LSSVM模型［4］形式:

式中:非线性映射函数φ(·)将输入数据映射到高维特征空间ω∈Rn;b∈r;ω是一个可以调整的权重矢量;b是阈值。

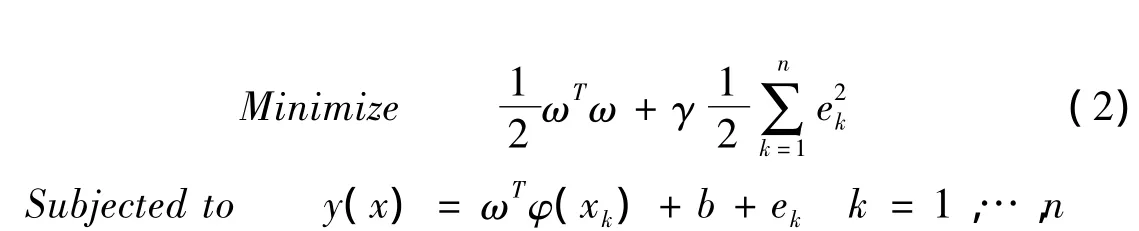
式中:γ是正规则化参数，控制误差样本的惩罚程度;ek是误差变量。

图1 最小二乘支持向量机结构

利用拉格朗日优化方法可以把上述优化问题转化为:

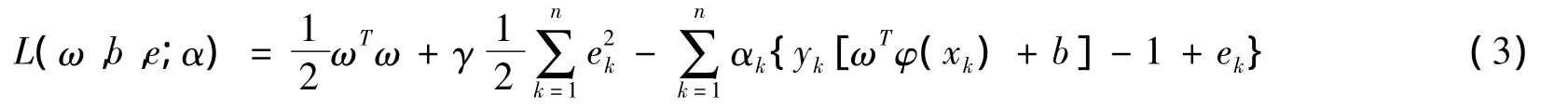
其中αi为与每个样本对应的拉格朗日乘子，容易证明解中只有少部分αk不为零，对应的样本就是支持向量。其具体的推导过程如下:

将上式中的ek和ω消去，最终归结为求解线性方程组，即:

式中:y= ［y1，···，yN］;1= ［1，…，1］;α = ［α1，…，αN］T;Ω = φ (xk)Tφ(xl)=k(xk，xl)，k=1，…，n，l=1，…，n，k(xk，xl)为核函数，选择γ ＞ ω确保矩阵Φ是可逆的，即:

最终可求得α和b，如下所示:

最小二乘支持向量机中的内积核函数和支持向量机类似，主要分为三类:(1)多项式核函数;(2)径向基核函数(RBF);(3)Sigmoid核函数。

本文采用径向基核函数，其形式为:

其中σ为高斯核函数的宽度。

最终最小二乘支持向量机的模型变为:

2 用Duncan-Chang本构模型的E-V模式模拟岩土的三轴实验

2.1 建立三轴实验模型

本文采用开发了的Duncan-Chang本构模型的E-V模式，对岩土的常规三轴实验进行有限元模拟，其采用的模型参数如表1所示。

采用的本构模型中的力学参数如表2所示。

表1 三轴实验模型尺寸 mm

表2 三轴实验力学参数

在有限元模拟的过程中，采用加载、缷载、再加载的应力加载方式，在模型底部约束其轴向自由度。根据Duncan-Chang本构模型的模量定义，当σ3=0时，模量都为0，这显然与实际不符，所以在施加压力之前，在ABAQUS的“初始步”中加相等的围压和反压，建立初始自平衡应力状态，然后再施加荷载。

2.2 数值模拟结果及对比分析

根据上述模型参数并结合ABAQUS中UMAT进行数值模拟，从模拟的结果中选取一个单元中的一个积分点的数据进行分析。用最小二乘支持向量机拟合此单元积分点的轴向应力与轴向应变关系曲线和主应力差与轴向应变关系曲线，图1中采用正则化参数γ=1.902×106，核函数宽度σ=0.033 6，图2中采用的正则化参数为γ=2.103 2×104，核函数宽度σ =0.028 1。

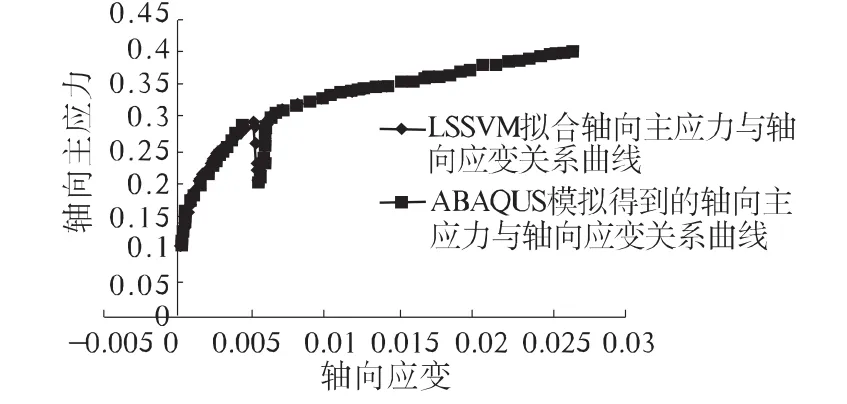
图1 单元积分点的轴向应力σ1与ε1轴向应变关系曲线

图2 单元积分点的主应力差与轴向应变关系曲线

3 结论

从上述结果可以看出，LSSVM拟合出的岩土的应力－应变曲线与原曲线几乎一致。所以，LSSVM在有限样本的情况下能够很好地进行函数曲线拟合，但是训练之前的参数选择是非常重要的，不同核函数的类型、核函数中参数和正则化参数选取都将直接影响函数的拟合效果甚至得不到理想的结果。LSSVM克服了SVM和ANN的诸多不足，在函数的拟合和预测中有着显示出自身独特的优势。因此LSSVM在岩土力学中将会得到越来越广泛的应用。

［1］CORTES C，VAPNIK V.Support-vector network［J］.Machine Learning，1995，20(3):273－297.

［2］Suykens JA K，Vandewalle J.Least square support vector machines classifiers［J］.Neural Processing Letters(S1370-4621)，1999 ，9(3):293 －300.

［3］赵洪波.岩土力学与工程中的支持向量机分析［M］.北京:煤炭工业出版社，2008.

［4］Pijush Samui，Sitharam T G Least-Square support vector machine applied to settlement of shallow foundations on cohesionless soils［J］.Int J Numer Anal Meth Geomech，2008(32):2033 －2043.

［5］费康.ABAQUS在岩土工程中的应用［M］.北京:中国水利水电出版社，2010.