溶洞地基稳定性模糊综合评价法综述

吴明鑫，李伍平

（广州大学土木工程学院，广州510006）

0 引言

在我国，岩溶地貌分布面积非常广，而溶洞是岩溶地貌中最常见的一种形态，随着近年来国家越来越多的工程建立在溶洞地基上，溶洞地基的稳定性评价便成了工程安全中最重要的问题之一。目前，对于溶洞地基的稳定性评价，国外有学者［1］将岩溶和结构作为一个系统，用可靠度的方法对岩溶和结构2个子系统分别进行分析，再通过调查对岩溶灾害进行预测评价，得到了较好的结果。国内则大多根据《建筑地基基础设计规范》与《岩土工程勘察规范》有关规定［2－3］和一些经验公式进行相关验算的方法来进行评价，刘之葵［4－5］指出影响溶洞地基稳定性的因素有岩层、洞体形态、地下水等因素，现有规范推荐的方法，没有考虑下覆溶洞的规模尺寸、地基土层等因素对地基稳定性的影响，由于影响溶洞地基性稳定性的因素众多，而且许多工程方面的数据模糊性较强，使得溶洞地基稳定性评价结果的准确性受到了影响。模糊综合评价法是一种基于模糊数学的综合评标方法，它是在模糊的环境中，考虑多种因素的影响，然后对事物或对象做出一个总体的评价。此方法能够考虑更多影响溶洞地基稳定性的因素，使得评价系统更全面、更真实、更准确。

1 模糊综合评价法

模糊数学又称Fuzzy数学，是一种研究和处理模糊性现象的数学方法。它的诞生始于1965年美国加利福尼亚大学控制论专家扎德（L.A.Zadeh）教授发表的《模糊集合论》，模糊数学于1976年传入我国，在这几十年中模糊数学的发展相当迅速，它的应用几乎涉及国民经济的各个领域。综合评价是综合考虑多种因素影响的事物或系统对其进行总的评价，当评价因素具有模糊性时，这样的评价称为模糊综合评价法，它包括一级综合评价法和多级综合评价法，其中一级综合评价法包括单因素评价法和多因素评价法。模糊综合评价法的主要步骤为：（1）首先确定评价因素体系，对评价对象建立因素集U＝｛u1，u2，...，un｝，再对ui进一步地划分ui＝｛ui1，ui2，....，uij｝，若uijk包含多种因素，还可以再分。（2）确定评语等级论域，例如地基稳定性V＝｛稳定性好，基本稳定，稳定性差，稳定性极差｝。（3）确定评价因素权重向量A，它代表评价因素在被评对象中的相对程度。（4）构造单因素矩阵R，它是单因素评价的结果。（5）选择合成算子进行一级模糊综合评价。（6）进行多级模糊综合评价，得到总的评判结果。

2 模糊综合评价法在溶洞地基稳定性的运用

2.1 模糊综合评价法在溶洞地基稳定性的运用现状

由于模糊综合评价法的准确性、真实性，越来越多的人把它用于溶洞地基稳定性当中，如陈春霞［7］对昆明新机场航站区各工程地质分区的地基稳定性影响因素及其层次关系进行了分析，建立了各因素影响下场地地基稳定性的模糊综合二级评判模型。孙鹏［8］运用模糊综合评价法对昆明新建机场方案三区的地基建立了数学模型，并对其岩溶地基稳定性进行了科学的评价。殷正钢和唐礼忠［9］根据影响岩石地基稳定性因素的模糊性和层次性，建立了岩石地基的稳定性评价的二级模糊评判数学模型，并通过实际工程验证了方法的有效性。赵明华等［10］将模糊集理论和工程地质勘察资料结合对某桥梁基桩桩端的溶洞顶板稳定性建立了模糊综合评判模型，并用于某实际工程，评判结果与实际情况相符合。程晔等［11］基于某工程实际资料，综合运用层次分析方法和模糊多属性决策方法，建立了岩溶区路基下溶洞顶板稳定性分析的模糊多层次多属性决策模型，通过实例表明，此方法合理有效。曹文贵等［12］运用模糊综合评价法与层次分析法对潭邵高速公路岩溶路段的溶洞进行了研究，为实际岩溶处理决策提供了可靠的手段。吴野［13］提出各影响因素的隶属度函数，并给出各连续和离散评价指标相应的隶属值，运用模糊综合评价法对贵州毕节机场各个工程分区的溶洞进行了评价，评判结果与定性、定量法评价结果具有一致性。

2.2 溶洞地基稳定性评价指标体系

从系统理论的观点出发，溶洞地基是一个复杂的系统，影响溶洞地基稳定性的因素众多，不可能只用单个指标来进行评判，因此在指标体系确认前，必须知道有哪些因素对溶洞地基稳定性会有影响。Hatzor，Y.H［14］提到几个控制浅层溶洞稳定性的岩石力学参数，它们分别是岩层覆盖的厚度、洞的跨度、结构面抗剪强度、岩石的强度、地下水条件等，蒋冲等［15］通过突变理论对影响溶洞顶板稳定性的主要因素进行了深入的探讨，这些因素有溶洞顶板厚度、溶洞跨度、荷载大小等。刘国喜［16］采用理论计算和数值模拟相结合的方法，分析了影响溶洞稳定性的因素有溶洞几何形状、桩径大小、荷载等，刘之葵［17］提到地质构造、结构面、岩层性质、溶洞洞体形态、地下水等是定性评价溶洞地基稳定的重要因素，用弹塑性理论推求了含溶洞岩石地基稳定性的计算公式，并作出洞体直径和洞体形状对地基稳定性影响很大的结论。刘会武［18］指出应根据溶洞与溶隙所处的位置、大小、埋深、顶板厚度、围岩的结构与强度、洞内堆积物及岩溶水活动等因素对岩溶地基稳定性进行分析与评价。由此可见，溶洞几何形状、荷载情况、地质构造、结构面、岩层性质、地下水、埋深厚度、顶板厚度等因素跟溶洞地基的稳定性有一定的联系。

文献［13］采用二级综合评价法将溶洞地基稳定性指标体系分为岩层情况、溶洞影响、构造影响3个大因素，而岩层情况又包括层状、风化程度、完整性、抗压强度，溶洞影响包括溶洞高度、跨度、顶板厚度、充填情况，构造影响包括裂隙发育情况、结构面状况。总共分了11个子因素进行一级综合评价。文献［7］则将溶洞地基稳定性评价指标分为4个大因素，它们分别是地层及岩性、断层影响、岩溶影响、力学性质，然后又将地层及岩性划分为岩组类型和风化程度，断层影响划分为裂隙发育情况和结构面性状，岩溶影响划分为溶蚀发育情况、岩溶顶板厚度、溶洞高度、溶洞跨度、溶洞充填情况，力学性质划分为承载力、变形模量和岩石单轴抗压强度。总共分了12个子因素进行一级综合评价。文献［8，12，19］也有此类型的划分。对于不同的实际工程，就对应着不同的地质环境，指标体系的确定也就可能不尽相同，上述几篇文献对溶洞地基稳定性模糊综合评价的指标体系各不相同，但是却有很多共同的因素。本文参照相关文献，根据影响溶洞地基稳定性普遍存在的因素做出如下评判指标体系：（1）溶洞情况，包括溶洞高度、溶洞跨度、溶洞充填情况、溶洞顶板厚度；（2）岩层情况，包括层状构造、岩芯完整度、岩石风化、溶蚀发育情况、岩层厚度、单轴抗压强度；（3）构造情况，包括结构面状况、裂隙发育。但是对实际工程的评价还是应该根据实际情况确定评价指标体系。

2.3 评判隶属函数的确定

隶属度是模糊数学在应用中用来描述事物的模糊界限的，对于隶属度的确定首先应该确定其隶属函数，而隶属函数的确定方法有模糊统计方法、指派方法、专家法、二元对比排序法等多种，如何选择合适的隶属函数便成为模糊数学在应用中的一个基本问题。对于要评价的模糊系统，常常把评价的因素按其数据特征（实数和特征状态）分成离散型变量和连续型变量。在上述溶洞地基稳定性的指标体系中，离散型变量有溶洞充填情况、岩石风化、层状构造、岩芯完整度、溶蚀发育情况、岩层厚度、结构面状况、裂隙发育，其余为连续型变量。目前，离散型变量隶属度的取值一般根据Γ统计原理，采用专家打分法确定，然后在隶属度取值表赋值。而对于连续型变量，则根据其数据的分布特征选择适合的函数类型，再求得其隶属度量化值。模糊理论中的隶属函数分布形式有正态型分布、梯型分布、岭形分布、柯西分布、矩形分布、Γ分布等。下面介绍在溶洞地基稳定性评价中经常用的3种模糊分布［20］（设μA（x）为模糊分布）：

（1）正态型分布

降半正态分布：

升半正态分布：

对称型正态分布：

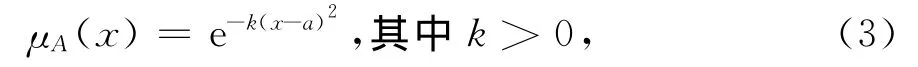
（2）梯形分布

降半梯形分布：

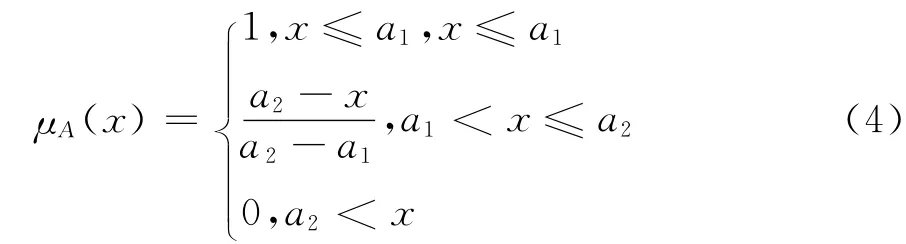
升半梯形分布：

对称型梯形分布：

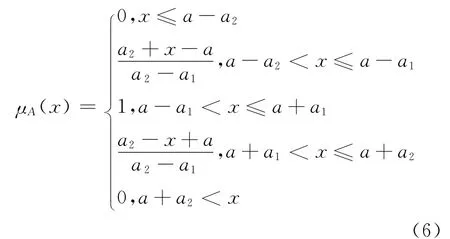
（3）Γ分布

降半Γ—分布：

升半Γ—分布：

尖Γ—分布：

2.4 权重的确定

权重是针对某一指标而言，它是指该指标在整体评价中的相对重要程度。溶洞地基各因素权重的确定是整个评价过程中比较重要的一个过程，权重的取值对整个评价结果有着直接的影响，因此必须客观准确地确定权重值才能对溶洞地基稳定性做出科学的评价。确定权值的方法有很多种，如调查统计法、专家评分法、层次分析法、公式法、灰色关联分析法等。

下面介绍几种在溶洞地基稳定分析中常用的方法。

（1）专家评分法，它是由若干专家根据自己的专业知识和经验对某个对象的各个指标的重要性进行判断，并给出各指标的评价分值，然后对专家意见进行归纳分析得出各指标的权重值。

（2）灰色关联分析法，是一种分析因素间关联程度大小的量化方法，它是根据各因素变化曲线几何形状的相似程度来确定关联程度的，若曲线形状越相似，则相应序列之间的关联程度越大，因此，可以用此方法来确定指标体系中因素的权重分配。

（3）层次分析法，是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代初提出的一种层次权重决策分析方法。其主要原理是将一个复杂的目标分解成多个目标或准则，从而分解为多指标的若干层次，再建立不同层次的同层因素两两比较判断矩阵，算出该矩阵的最大特征值及其所对应的特征向量，归一化后，得出不同层次不同因素的相对权值。

文献［21］高速公路下伏岩溶顶板稳定性二级模糊综合评判采用层次分析法、专家评分法和灰色关联分析法确定溶洞地基的各因素权重值，并得出溶洞宽度、顶板岩层厚度、岩石单轴抗压强度、裂隙发育情况对其稳定性有突出的影响。文献［22］基于专家调查法得出一级评判中溶洞宽度、顶板厚度、岩石单轴抗压强度对地基稳定性影响较大，二级评判中溶洞情况和顶板岩层影响较为突出。文献［12］采用层次分析法确定各因素权值的分配。文献［23］运用灰色关联分析法对岩溶地基各因素权重值进行了探讨。文献［13］采用专家打分法和灰色关联度得出一级评判中岩层厚度、溶洞跨度、顶板厚度、裂隙发育情况、结构面状况对溶洞地基稳定性影响较大，二级评判中溶洞情况和构造情况影响最为突出。虽然不同的实际工程当中，评判指标体系不一样，评价指标权重的方法不一样，各指标权重值也不相同，但是却反映了一些相同的情况。本文综合相关文献的描述得出，在岩溶地基稳定性评价中，一级评判中影响最为突出的因素为：溶洞跨度、顶板厚度、岩石单轴抗压强度、裂隙发育情况。

3 结语

本文介绍了近年来模糊综合评价法在溶洞地基稳定性的运用现状，从模糊综合评价法的基本原理出发，探讨了溶洞地基稳定性指标体系、隶属函数及权重方法的确定。在溶洞地基稳定性分析中，模糊综合评价法是一种新型的方法，它由于能处理大量的定性资料和模糊信息而得到了越来越多的应用，在该方法中，选择合理的隶属函数和权重值是溶洞地基稳定性评价的关键问题之一，但是隶属函数和权重的确定却存在着很强的主观性和经验性，因此，如何准确地确定隶属函数与权重值还有待进一步研究。

［1］lmachev V V To，eshchetkin O B N.Evaluation of Karst Hazards for Civil and Industrial Buildings［J］.Acta Geological Sinica（English Edition），2001，75（3）：269－274.

［2］GBJ 50007—2002，建筑地基基础设计规范［S］.

［3］GBJ 50021—2001，岩土工程勘察规范［S］.

［4］刘之葵，梁金城.岩溶地基稳定性评价中应注意的几个问题［J］.地球与环境，2005，33（z1）：440－444.

［5］刘之葵，梁金城.岩溶区溶洞及土洞对建筑地基的影响［D］.长沙：中南大学，2004：94.

［6］Zadeh L A.Fuzzy sets［J］.Information ＆ Control，1965，8（3）：338－352.

［7］陈春霞.昆明新机场航站区地基稳定性评价［D］.成都：成都理工大学，2008.

［8］孙鹏.昆明新建机场岩溶发育特征及其稳定性研究——以方案三区为例［D］.成都：成都理工大学，2007.

［9］殷正钢，唐礼忠.岩基稳定性的模糊综合评判［J］.山西建筑，2005，31（2）：47－49.

［10］赵明华，程晔，曹文贵，等.桥梁基桩桩端溶洞顶板稳定性的模糊分析研究［J］.岩石力学与工程学报，2005，24（8）：1376－1383.

［11］程晔，赵明华，曹文贵，等.路基下岩溶稳定性评价的模糊多层次多属性决策方法研究［J］.岩土力学，2007，28（9）：1914－1918.

［12］曹文贵，程晔，袁腾芳，等.潭邵高速公路路基岩溶顶板稳定性二级模糊综合评判［J］.公路，2003（1）：13－16.

［13］吴野.贵州毕节机场环境地质条件及场地稳定性评价［D］.成都：成都理工大学，2010：47－52.

［14］Hatzor，Y H，Wainshtein，etc.Stability of Shallow Karstic Caverns in Blocky Rock Masses［J］.International Journal of Rock Mechanics and Mining Sciences，2010，47（8）：1289－1303.

［15］JIANG Chong，ZHAO Ming－Hua，Cao Wen－Gui.Stability analysis of subgrade cave roofs in karst region［J］.Journal of Central South University of Technology，2008，15：38－44.

［16］刘国喜.岩溶地区大桥桩基下伏溶洞稳定性研究［D］.北京：北京科技大学，2005：65－66.

［17］刘之葵，梁金城，朱寿增，等.岩溶区含溶洞岩石地基稳定性分析［J］.岩土工程学报，2003，25（5）：629－633.

［18］刘会武，李芝军，陈卫兵，等.变电站岩溶地基的勘察设计与地基基础处理［J］.能源技术经济，2010，22（3）：45－49.

［19］张永杰，曹文贵，赵明华，等.岩溶区公路路基稳定性的区间模糊评判分析方法［J］.岩土工程学报，2011，33（1）：38－44.

［20］李洪兴，汪群，段钦治，等.工程模糊数学方法及其应用［M］.天津：天津科技出版社，1993：170－175.

［21］程晔，曹文贵，赵明华，等.高速公路下伏岩溶顶板稳定性二级模糊综合评判［J］.中国公路学报，2003，16（4）：21－24.

［22］程晔，赵明华，曹文贵，等.公路桥梁基桩桩端岩溶稳定性的模糊评价［A］.中国岩石力学与工程学会.第八次全国岩石力学与工程学术大会论文集［C］.北京：中国岩石力学与工程学会，2004：310－314.

［23］WU Ye，HUANG Run－Qiu，HAN Wen－Xi.Stability Evaluation Method for Karst Cave Roof Based on Fuzzy Theory［J］.ASCE Conf.Proc.2011，419（41184）：296－296.