东北虎年饲食量与年龄关系的分析及数学模型

张秀娟 韩书霞 陈 洁

(东北林业大学，哈尔滨，150040)

东北虎(Aumr Tiger)也叫西伯利亚虎、阿穆尔虎(黑龙江的俄语名称为阿穆尔河)、乌苏里虎、满洲虎等，是国家Ⅰ级重点保护动物，历史上曾广泛分布于中国东北地区［1］。东北虎现在已成为极度濒危的物种。早在20世纪50年代以前，一些外国学者就曾对我国境内的野生东北虎有过报道，并作了详细的记述。进入80年代，对东北虎的研究工作广泛开展，并且扩展到各个领域，主要涉及东北虎的分布及数量、生态、生理生化、饲养繁殖、疾病等方面。在对东北虎饲养繁殖的研究中，主要侧重其繁殖行为方面，对其饲养方面的研究尤其是对饲食的研究极少。而人工饲养作为对东北虎进行迁地保护的一项重要措施，对其饲食方面的研究则必不可少。同时，黑龙江东北虎林园是世界上最大的人工饲养繁育东北虎基地，2006年该园人工饲养的东北虎就已超过700只［2］，现在可达1 200多只，如此庞大的数量更意味着饲养经费支出巨大。因此，对东北虎进行饲养方面的研究更具有极其重要的现实意义。

1 研究地区自然概况

黑龙江东北虎林园位于哈尔滨市松花江北岸的松北新区，地理坐标为东经 126°16'～126°21'，北纬45°29'～45°30'，属温带大陆性季风气候，年平均气温3.0℃，年降水量500 mm左右，平均风速3 m/s，无霜期120 d，年平均日照2 630 h。

林园的围栏高4.25 m，围栏内的植被以灌木和草本为主，兼有少量乔木。植物组成主要包括杨(Populus spp.)、柳(Salix spp.)、暴马丁香(Sringa reticulata)、胡枝子(Lespedeza bicolor)、榛子(Corylus heteropphylla)、苔草类(Carpes spp.)、莎草类(Cyprus spp.)、羊草类(Aneurolepidium spp.)等。围栏内有人工修建的水塘，供东北虎游泳、消暑和饮用。

2 研究方法

2.1 耗散结构理论与熵

比利时物理化学家普利高津在1969年提出了耗散结构理论，并由此荣获了1977年度诺贝尔奖［3］。耗散结构理论是研究开放系统在远离平衡态情况下演变规律及性质的科学。耗散结构理论中最重要的概念就是熵。熵变(生命熵)公式可写作:

dS=dSe+dSi。

式中:S表示熵;dS表示dt时间内生命体系的熵变;dSe表示dt时间内生命体系通过代谢活动(与外界交换能量、物质和信息)由外界引入的熵，其值可正、可负亦可为零;dSi表示dt时间内生命体系内部产生的熵，是由生命体内部各种不可逆过程引起的，其数值恒为正。

2.2 东北虎与耗散结构系统

东北虎本身就是一个高度有序的耗散结构系统，其机体系统的熵值取决于生命活动所产生的熵与机体同外界环境相互作用时所形成的熵的和，健康状态下东北虎机体处于低熵状态或负熵状态。东北虎要不断地从外界摄取食物、水、O2等，同时向外界排放粪便、汗水、CO2等，并与环境交换热［4］。东北虎在新陈代谢过程中，体内无时不在进行着溶解、渗透、混合、扩散、流动与各种化学反应的不可逆过程，使dSi＞0。东北虎要正常成长，必须要引入大量的负熵流。负熵流的引入分两部分:一部分是热交换引入，通常东北虎体温高于环境温度，它在新陈代谢过程中，产生大量的热，要维持正常体温，就要不断向环境散热，使这部分引入熵为负;另一部分是物质交换引入，东北虎摄取的食物主要是淀粉、糖、脂肪、蛋白质、纤维素等高聚合物，它们分子量大，排列有序，熵值比较小，在体内经过物理与化学变化，有的被吸收，有的被排出体外，排出的渣汁、CO2等分子小，熵值大，这样就使这部分熵引入也为负熵流。即东北虎摄取食物就相当于补充负熵。

3 结果与分析

3.1 数据收集及处理

试验研究的东北虎机体负熵流的引入，主要是物质交换引入部分。

野生东北虎以野猪、鹿、麅等为食。而人工饲养的东北虎则以牛、鸡肉为主，牛奶、鸡蛋、鱼肝油、骨粉及维生素等为补充饲料。

通过在东北虎林园虎日志资料的5次取样，并对每只东北虎日饲料进行统计，确定以13只东北虎为研究对象，并将它们分别编号为虎1，虎2，…，虎13。其中，虎1至虎12用于试验研究，虎13作为对照组，并且所取试验组的虎寿命均为13岁，对照组虎的寿命为15岁。在统计的过程中，对一年内日饲料量叠加得当年年饲料量。由于东北虎2岁后离开母虎独立生存，故样本虎年龄从2岁开始记录。试验组东北虎年饲料量与年龄的统计数据如表1所示，对照组东北虎年饲料量与年龄的统计数据如表2所示。

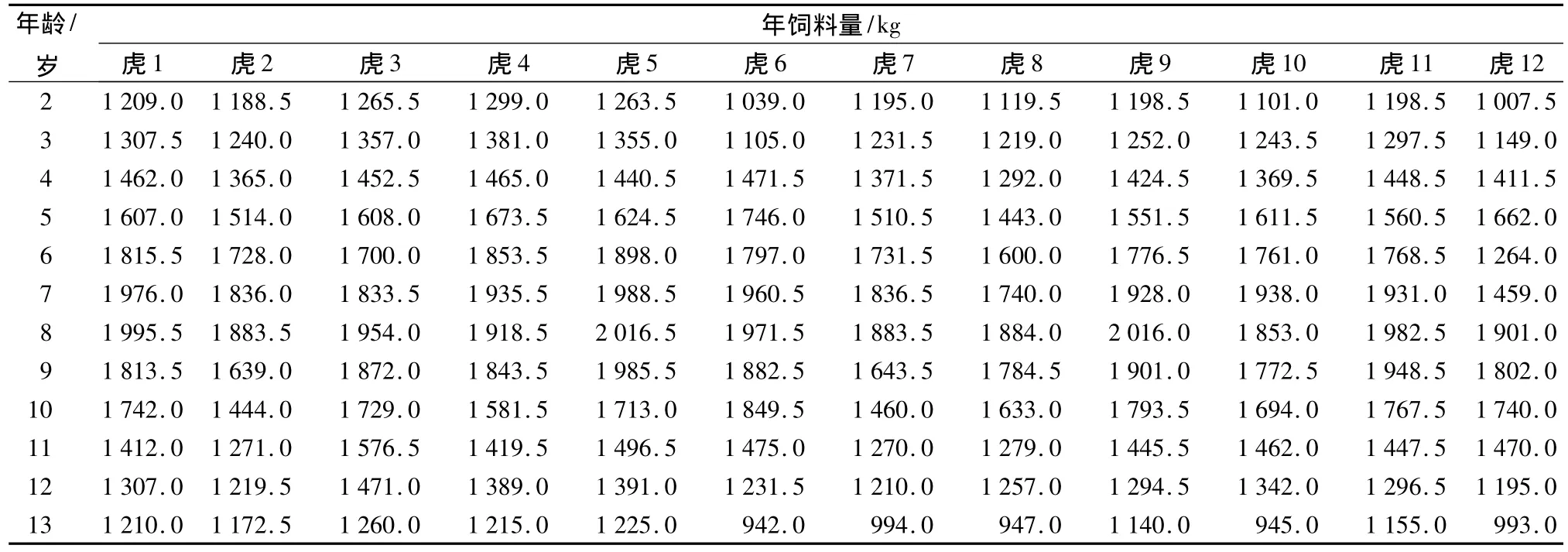
表1 试验组东北虎年饲料量的统计

表2 对照组东北虎年饲料量与年龄的统计

3.2 数据分析

利用Excel软件以东北虎年龄为横轴，年饲料量为纵轴，画出散点图如图1所示。

整个东北虎生命系统的耗散过程可概括为:低级有序—高级有序—低级有序—无序—死亡。可以独立生存的2岁东北虎，机体相对处于低级有序状态，内部各项功能尚待完善。要使东北虎健康成长，机体向高级有序发展，必须积极引进负熵流，打破现时的有序。

由图1可以看出，在东北虎初期成长阶段即图中的第一部分，东北虎随着年龄的增长对饲料的需求量也逐年增加，此时，东北虎机体为了满足生长发育的需要，进食量加大，从外界获得的负熵大于机体内部熵的产生，即dSi＜－dSe，系统的总熵减小，机体内部系统从低级有序结构向高级有序结构演化，机体功能日益完善，可以理解为东北虎的“青年时期”。

在东北虎生长到一定阶段即图中第二部分时，随着年龄的增长，饲料用量的增减变化不明显，趋于稳定，此时机体从外界获得的负熵流等于体内的熵产生，即dSi=－dSe。由此可以看出，机体内部的熵产生，每增加一个单位就需要一个单位的负熵流来抵消它的影响。此阶段机体系统的总熵不变，处于高级有序状态，理解为东北虎的“壮年时期”。此时期，只要饲食结构合理，饲料量保持稳定，尽量减少外界的扰动，如疾病等，东北虎就会健康生存。

随着年龄的增长，东北虎机体功能开始退化，并极易受外界影响，机体系统开始从高级有序向低级有序转化，逐渐步入老年化，进入“老年期”即图中的第三部分。在这一阶段，东北虎的年饲料量随着年龄的增加而缓慢减少，机体从外界获得的负熵流小于内部熵的产生，即dSi＞－dSe，系统的总熵增大。当总熵最大时，东北虎机体高度混乱、无序，有序的生命活动已经无法维持，东北虎逐渐走向死亡。

由于东北虎个体之间存在差异性，不同东北虎的“生命三阶段”的跨度不一，但整体走势不会变。

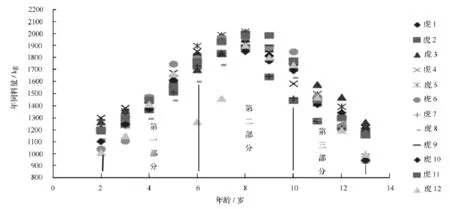
图1 东北虎年饲料量与年龄关系的散点图

3.3 建立模型

3.3.1 模型估计

从图1可以观察到，东北虎年饲料量与年龄关系的散点图大致呈抛物线状，因此，可以用二次多项式模型来模拟年饲料量与年龄的关系。

设东北虎年饲料量为因变量y，年龄为自变量x，并设此模型为:

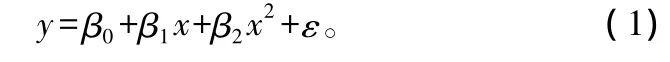
式中:β0为常数项;β1、β2分别为一次项系数和二次项系数;ε为随机误差。

将式(1)的多项式回归模型转化为多元线性回归［5］。令:x1=x，x2=x2，则(1)式化为:

根据表1数据，年饲料量为因变量y，年龄为自变量x1，年龄的二次方为自变量x2，并应用SPSS软件计算回归方程，结果见表3。

表3 模型拟合结果

根据表3可得回归模型为:

R2=0.814，拟合度较高。F=308.357≫F0.05=(2，9)=4.26，显著性 P≈0，说明因变量与自变量线性关系显著。

综上，得东北虎年饲料量与年龄关系的模型为:

3.3.2 模型检验

应用式(3)的回归模型预测2～15岁东北虎的年饲料量并与对照组进行比较，得出相对误差，如表4所示。从表4可知，由回归方程得出的预测值与实际值的误差最大为3.8%，最小仅为0.2%，回归方程具有较高的预测精度，可以认为预测值与实际值是一致的。这说明应用二次多项式预测东北虎年饲料量与年龄的关系比较有效。

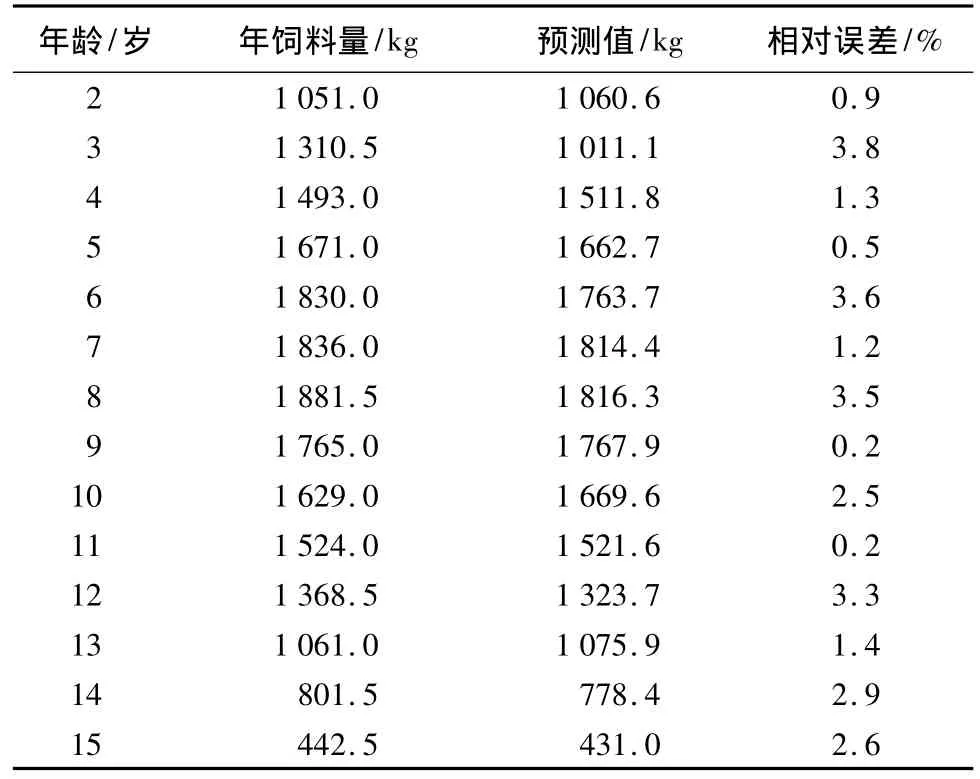
表4 预测值与相对误差

4 结论

东北虎本身就是一个耗散结构系统，摄取食物的过程就相当于补充负熵，因此，可以根据其进食情况判断体内熵的变化情况。以便饲养员及时找出对策，改变东北虎体内的熵值，使其健康生长。

东北虎从生长发育到死亡这一过程中，年饲料量与年龄表现出明显的二次多项式关系。试验证明，回归方程具有较高的拟合度，并且，预测值与实际值误差极小，可以为今后东北虎的饲养提供一定数据帮助。

［1］郭玉荣，邹红菲，吴庆明，等.黑龙江东北虎林园管理策略探讨［J］.野生动物，2007，28(1):36－38.

［2］马逸清.东北虎分布区的历史变迁［J］.自然资源研究，1983(4):44－48.

［3］沈小峰.耗散结构论［M］.上海:上海人民出版社，1987.

［4］张德生.熵定律对不同体系的应用［J］.安庆师范学院学报，1998，4(1):94－97.

［5］何晓群，刘文卿，应用回归分析［M］.北京:中国人民大学出版社，2007.