外圆弧半径测量误差分析
张晓永,李晓庆,尚生华
(总装备部武汉军事代表局驻焦作地区军事代表室,河南 焦作 454001)
1 测量计算及误差分析
当被测件尺寸不是很大时,通常采用如图1 所示方法测量外圆弧半径[1],即将被测外圆弧放在平板上,两侧各放置相同直径为D 的精密圆柱,采用适当精度的测量工具测量出两圆柱外边缘距离M,即可计算出被测件的外圆弧半径R。

图1 外圆弧测量示意图
由图1 直角三角形ABO 可以得出如下关系式:
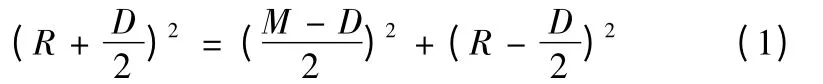
整理式(1)可得

由式(2)结合图1 可得

对式(2)全微分可得

在测量时,辅助设备本身存在的误差及测量过程引进的误差对测量结果产生的影响为

其中:ΔD 为精密圆柱体自身的误差,亦可用其加工公差代替;ΔM 为横向距离测量误差(由测量人员、测量环境等因素决定)。根据误差理论[2]有
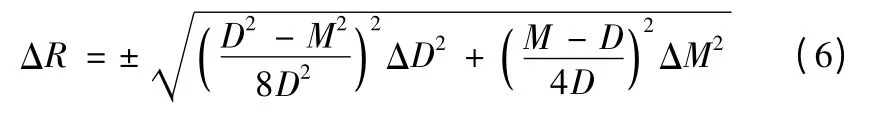
由式(6)可以得出以下结论:
1)测量精度由辅助精密圆柱体本身的加工精度及距离测量误差所决定,而测量误差的影响比精密圆柱体所引起的误差大得多,因此实际测量过程中,应尽可能减小这种横向测量误差。
2)当辅助设备精度及距离测量误差一定时,测量精度还与精密圆柱体直径有关,即与两圆柱体外边缘距离M 和圆柱体直径D 的比值有关。图2 为当横向测量误差ΔM=3 μm,ΔD=2 μm 时的外圆弧测量误差变化曲线。从图2 中可以看出,测量误差随着比值的变大而变大,即测量误差随着辅助圆柱体直径的变大而变小,因此在实际测量时应尽可能选取具有较大直径的辅助圆柱体。
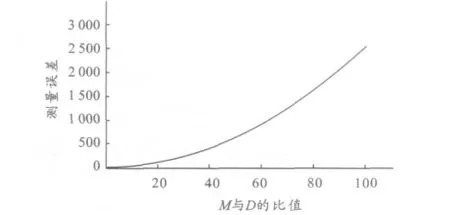
图2 外圆弧测量误差变化曲线
2 精密圆柱体最小直径的确定
2.1 理论分析
从以上分析可以看出,欲减小测量误差,提高测量精度,除减小仪器测量误差外,还必须根据被测外圆弧的结构尺寸,选取具有合适直径的精密圆柱体,换言之,为达到满足要求的测量精度而确定圆柱体直径。
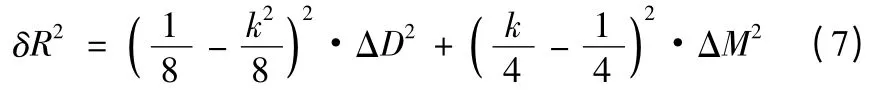
根据给定的测量精度值,求解上式中的k 值。利用此值便可确定所需的圆柱体的最小直径。
2.2 应用实例
设一外圆弧样板R =30 mm,其公差要求为±0.04mm,以其20%作为测量误差,横向测量误差ΔM =3 μm,ΔD =2 μm。下面介绍为满足测量需求,辅助圆柱体最小直径的选取过程。
由上述可知,δR =ΔR·20% =0.04 ×0.2 mm =8 μm。将其代入式(6)可得
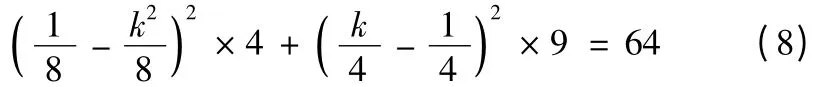
3 结束语
在实际工作中,有时会遇到工件结构尺寸限制问题(如工件的弓高相对较小),这时需要考虑该方法所确定的最佳精度,以便判断该测量方式是否适合实际应用,其判别方法与最小直径确立方法类似,本文仅提供一种分析方法。
[1]徐刚,徐沁泉. 平台测量[M]. 北京:中国计量出版社,1998.
[2]中国兵器工业质量协会.实用统计技术方法[M].北京:兵器工业出版社,2003.

