卡尔曼滤波在红外寻的导弹被动制导中的应用
龚冬梅,张海涛,龚 梅
(中国空空导弹研究院,河南 洛阳 471009)
随着科技特别是航空航天技术的发展,空中目标机动突防性能逐渐提高,其拦截问题引起了世界各军事强国的普遍重视[1]。早期的拦截器由于弹载计算机计算速度慢以及古典导引律本身缺陷等原因而使得制导精度不高,致使其无法在实战中应用。因此,从20 世纪的70年代起,依靠状态空间法、变结构理论以及其他智能方法等发展起来的先进制导律在理论研究中表现出比传统比例导引律具有明显的优点,主要表现是理论严谨,命中精度很高。但这些先进制导律优点明显,但缺点同样显著,其使用的前提需要目标以及导弹的状态信息多,这在实际应用中相当困难,尤其是对于红外空空导弹来说,仅能够测量出角度和角速度信息,而弹目相对距离、相对速度和目标加速度信息无法测量,只能靠估计得到。这些仅利用角度信息来估计出弹目相对运动状态信息实际上就是一个滤波问题。本文利用最优卡尔曼滤波方法,对仅有的失调角信息进行滤波状态估计[2-5],在简化制导回路上以古典比例导引律和扩展比例导引律为例,进行数值仿真,计算结果表明,将通过滤波估计出的弹目相对速度,视线角速度和目标加速度等信息应用于扩展比例导引律的系统与纯比例导引律相比,具有更小的脱靶量。
1 目标运动方程的建立
目标运动参数估计方程在惯性系中建立,采样时间设计为Ts,将方程离散化:

即状态方程为:

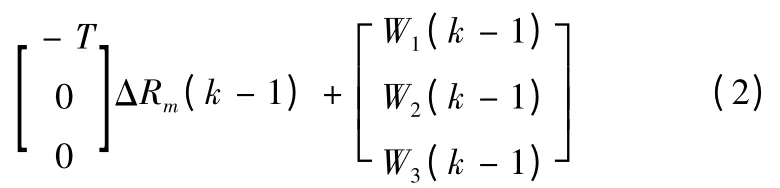
式中:ΔRm、TT、T、W 分别为导弹速度增量、目标机动时间常数、步长、状态噪声。
其中目标机动模型采用一阶马尔科夫过程的假设
测量方程:

即:

式中~R0、V1分别为相对距离测量量和量测噪声。
导引头对目标的探测信号中含有多种噪声,即状态噪声w 包括背景噪声、热噪声、电磁噪声、探测噪声等,对于采用比例导引的导弹,导引头量测误差v 主要有目标相对导弹的视线角速度的量测误差,失调角零位的测量误差,引起失调角零位测量误差的因素较多,如导引头信息处理误差,导引头装配误差,通道耦合误差,干扰、背景引起的误差,弹体耦合误差,陀螺回转中心与位标器质心不重合引起的漂移,随动机构间隙等,这些因素都会引起信号测量值的波动。因此,为提高制导精度,加强对大机动目标的攻击能力,在制导回路中加入滤波算法以保持制导信号的稳定以及制导状态信息的重构就显得尤为重要。
2 卡尔曼滤波器设计
采用卡尔曼滤波公式,其最优滤波方程为:



为误差方程。

可得滤波方程:
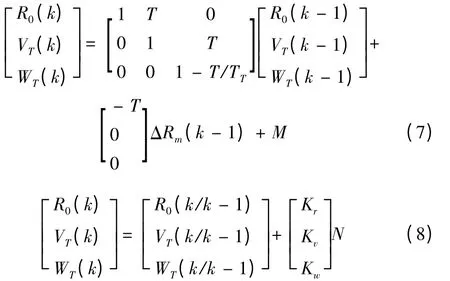
其中:
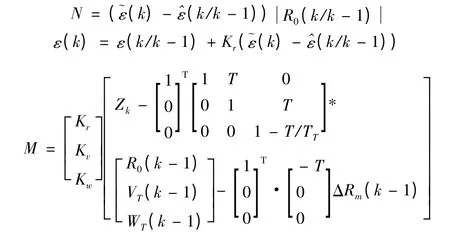
在此模型中,视线角的测量包含有噪声,通过将视线角测量值与导弹到目标距离的估值相乘可以产生相对位置的伪测量值,通过卡尔曼滤波器产生相对位置、相对速度和目标加速度的最优估值,如图1 所示,量测值~εR 是光轴与真值之间的距离,估值^εR 是估值与光轴之间的距离,线偏离ΔRI=(~ε+Δ~ε)R-^εR,在导引头成像系统中,伺服机构驱使光轴跟踪真实值,而估值通过线偏离的校正始终跟随光轴运动,所以在滤波角通道系统中,只要准确估计出DRI,可得到Y,Z 向上的状态。
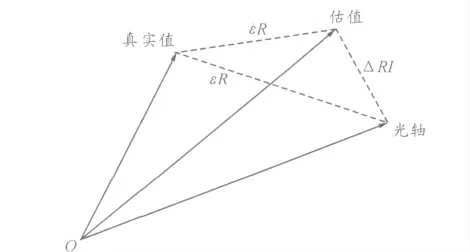
图1 真实值与估值之间的关系
由于ε 在惯性系中,因此在使用时要转到视线系,这就实现了相对距离、目标速度、目标加速度和失调角的卡尔曼滤波估值。工程实际使用时,要考虑滤波门限的选取、距离分档、测量噪声的设计和目标类型等因素对协方差阵P 的影响,要对协方差阵P 调整以保证滤波的精度和收敛性。
3 数值仿真
仿真条件如下:状态和量测方程如上所述,仿真时间从0 ~10 s,采样时间ts=0.01 s,输入为正弦信号,状态噪声Q和量测噪声R 的方差为0.4 和1,即w =sqrt(Q)* randn(n,1),v=sqrt(R)* randn(n,1),滤波增益阵的初值Mn=设为zeros(3,1),P 阵和x 的初值分别为B* Q* B'和zeros(3,1),滤波后的波形,量测噪声,卡尔曼滤波增益,卡尔曼滤波协方差阵的仿真结果如图2 所示。
经过数字仿真分析可以得出,在量测修正得当的前提下,卡尔曼滤波值可以准确并平滑的估计出状态变量,模型具有较小的超调时间,当采样间隔越小时,估值越平滑,越接近真实值,初始协方差阵P 是在解Ricatti 方程式中使用的,其初值对滤波具有很大的的影响,噪声越小滤波估值越准确,状态噪声增大时会严重影响到滤波的效果,在工程实际运用中噪声加入要考虑到敏感器件的实际情况。
有了这些状态信息,就可以改进导引律设计,以扩展比例导引律为例:
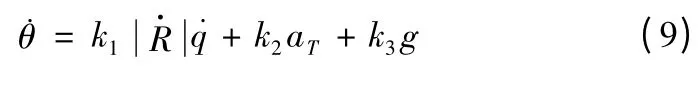
由脱靶量可以看出,从近距到中距,大离轴角发射,目标作6 ~9 个g 大机动飞行时,制导系统中加入滤波比纯比例导引脱靶量显著减小,有了滤波的准确估值可以大大改进制导系统的精确度,滤除噪声增加系统的稳定性。
4 结束语
本文主要研究了仅有角度测量信息的红外寻的导弹被动制导问题,给出了基于最优卡尔曼滤波的目标运动状态估计方法,并给出了简化制导回路下加入滤波扩展比例导引和不加滤波比例导引两种情况下制导系统仿真,可以得出以下结论:
(1)在量测修正得当的前提下,卡尔曼滤波值可以平滑准确的估计出目标状态变量。
(2)由脱靶量可以看出,制导系统中加入滤波后扩展比例导引比纯比例导引脱靶量显著减小,可以大大改进制导系统的精确度,滤除噪声增加系统的稳定性。
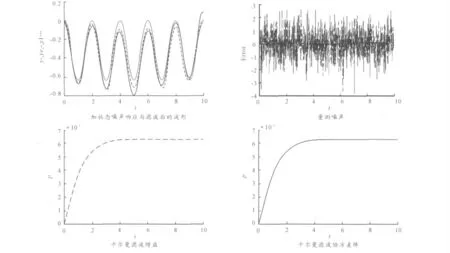
图2 减小采样时间后的滤波图形
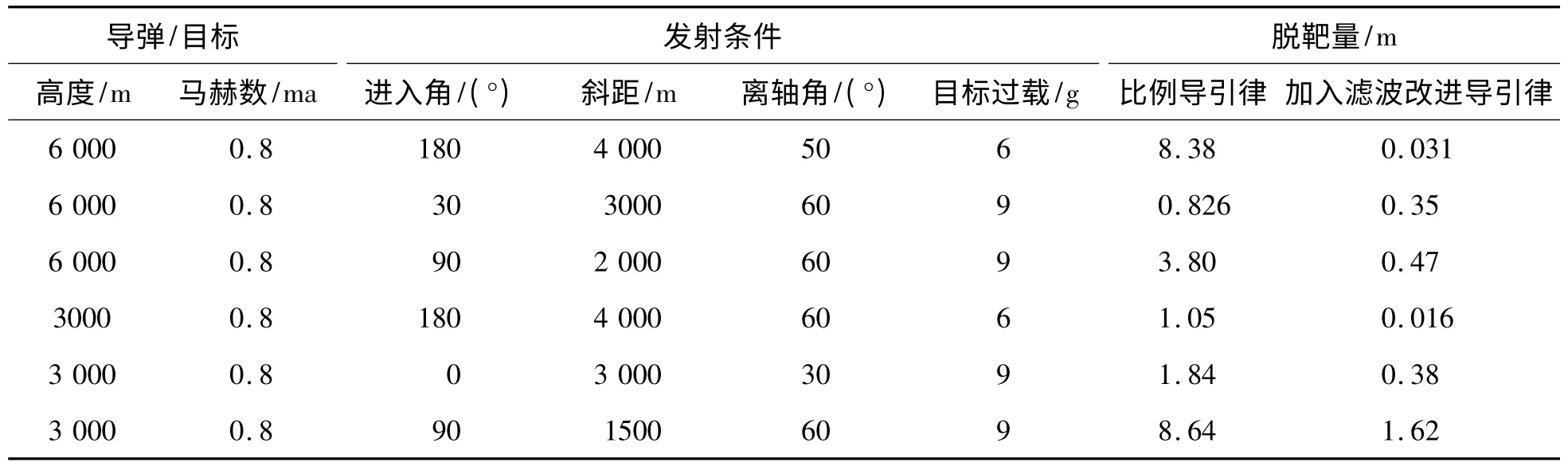
表1 不同仿真条件下两种制导律的脱靶量对比情况
[1]于翔川.基于非线性滤波的目标跟踪算法研究[D].西安:西安电子科技大学,2009.
[2]郑佳兴.卡尔曼滤波技术在捷联姿态测量系统中的应用研究[D].长沙:国防科学技术大学,2007.
[3]周荻.寻的导弹新型导引规律[M].北京:国防工业出版社,2002.
[4]周荻,胡振坤,胡恒章.自适应推广KALMAN 滤波应用于导弹的被动制导问题[J].宇航学报,1997,184(4):31-36.
[5]王剑,吴嗣亮,房秉毅.基于扩展Kalman 滤波的运动目标距离/速度联合估计[J].系统工程与电子技术,2007,29(7):1053-1050.
[6]谢春思,王敏庆,董受全,等.基于卡尔曼滤波的反舰导弹火控数据处理[J]. 火力与指挥控制,2009(5):95-97.

