上海光源红外束线中CVD金刚石窗的参数对红外透射率的影响

黄君艺 陈 敏 佟亚军 吉 特 张增艳 肖体乔

(中国科学院上海应用物理研究所 上海 201800)

红外光谱学技术在生物、化学、医学等领域均有广泛应用[1,2]。一些物质气体分子的振动转动谱，大分子(如蛋白质、核酸、醣类、脂类及生物膜结构等)的振动转动谱，晶态、非晶态固体的声子谱，电子能谱都在红外波段。研究这些红外光谱可知道物质的成份、结构和性质等，并能进行定性和定量分析。同步辐射光源克服了传统红外光源亮度低的缺点，极大提高了红外光谱的信噪比，亮度比传统黑体辐射光源高三个数量级以上。目前，国外同步辐射中心(如ALS[3], NSLS[4], Spring8[5], Soliel[6], CLS[7]等)共建有数十条红外线站。我国合肥同步辐射光源也建有一条红外光束线[8]。

在同步辐射红外光束线站中，储存环为超高真空，而实验站通常工作在高真空，为隔离储存环和实验站间的高低真空，需在束线中插入一个隔离窗来实现。由于天然金刚石窗价格昂贵，目前国际上红外束线大多采用 CVD金刚石作为隔离真空的窗口。上海光源正在建设的BL01B红外光束线也采用CVD金刚石作为隔离窗。金刚石窗有一定厚度，光束入射该窗口，部分光束在前后表面间发生多次反射，反射光相互干涉后导致不同波数的透射率发生变化。同步辐射红外实验站通常采用傅里叶变换光谱仪，对光强的变化非常敏感。为尽可能降低这种影响，需采取一些措施，因此，将CVD金刚石窗加工成具有一定楔角的楔型结构，以尽量降低这种影响。本文结合上海光源BL01B的光源特性，对金刚石窗的各个参数对红外透射率的影响进行系统分析，为同步辐射红外光束线的优化设计提供理论依据。

1 前后面平行的CVD金刚石窗对红外光束的影响[9]

光束经过 CVD金刚石窗时，前后表面会发生多重反射(图 1)。金刚石对整红外波段的折射率n=2.38(n随波长变化，但变化之小可认为定值)，设厚度为d，均匀光照且垂直入射。

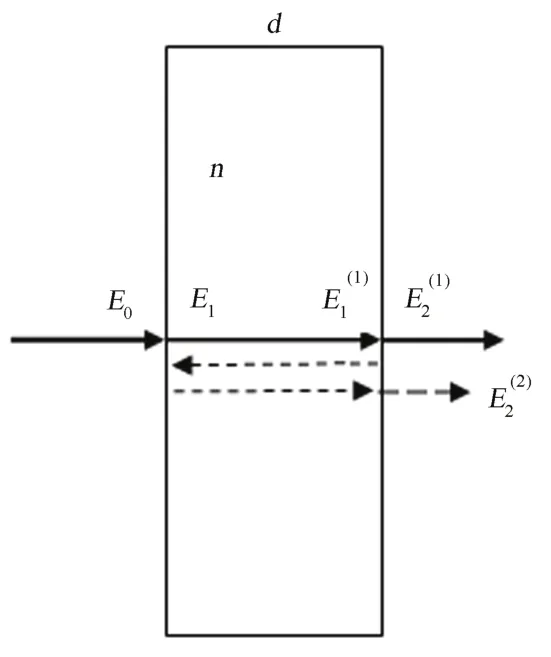
图1 CVD金刚石窗多重反射示意图Fig.1 Multiple reflections in the CVD diamond window.

从真空入射到金刚石界面的振幅透射率T1与从其界面出射到真空的振幅透射率T2为：

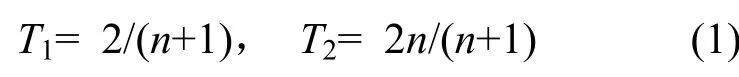
从金刚石界面到真空的振幅反射率R为：

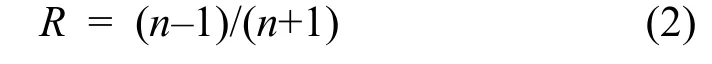
用E0表示初始光波场，则传播至第一界面后的光波场E1为：

传播到第二界面(即传播了距离d)后，E1的位相变化是exp(2πind/λ)，λ表示波长，忽略金刚石的吸收，光波场变为：

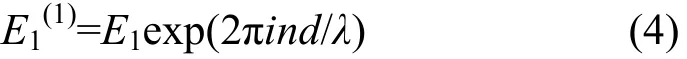
显然，部分光波会在第二界面反射，再传播到第一界面又产生反射光，如此反复，形成多重反射。而第一次射出金刚石的光波场E2(1)为：

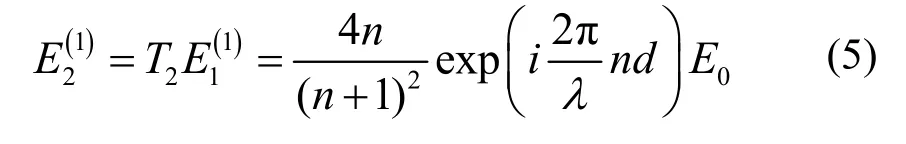
经计算可得到第m次射出金刚石的光波场为：

于是总的出射光E2为：

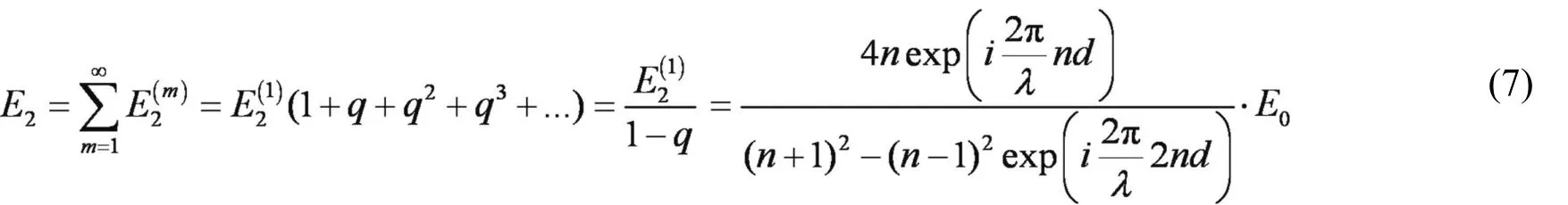
出射光与初始入射光的光强之比为：

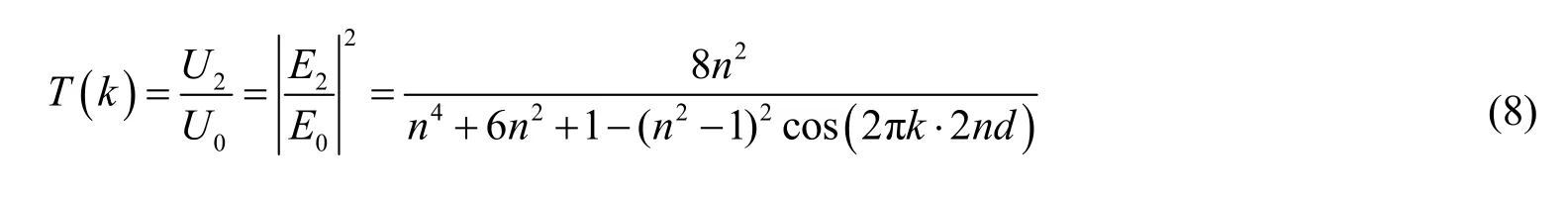
其中波数k=1/l。图2为均匀光照下，用式(8)计算所得透射率随波数的变化曲线，在0.5和1之间呈周期性变化，平均透射率是0.714(图中虚线)。

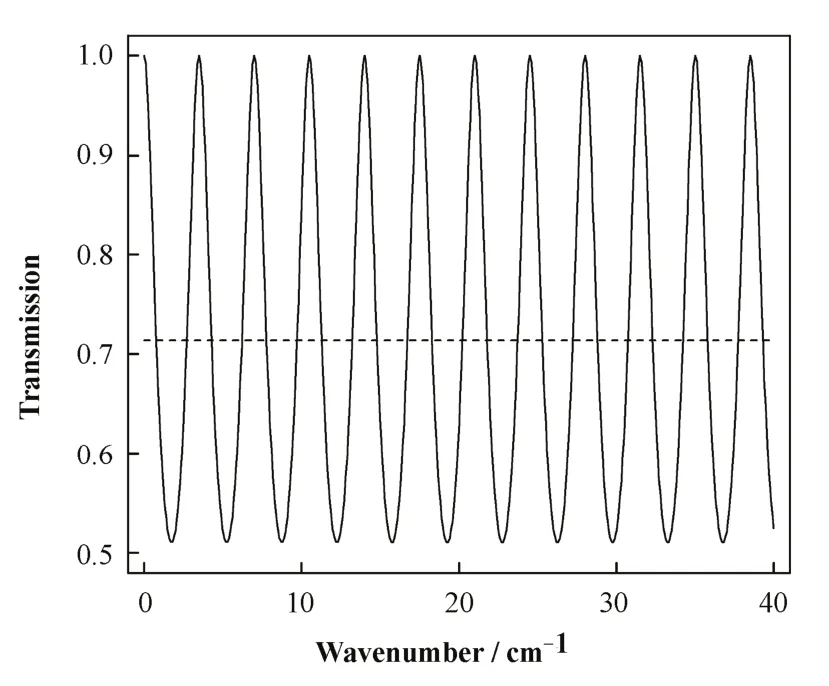
图2 前后面平行，厚度0.6 mm，直径25 mm的CVD金刚石窗透射率随波数的变化曲线Fig.2 Transmission as a function of wavenumber for a plane-parallel CVD diamond window with a thickness of 0.6 mm. The average transmission is 0.714(dash line).

这种由多重反射现象引起的透射率周期性变化会对光束进行有害地调制，必定会给光谱带来噪声，最终影响光谱质量。

2 有楔角的CVD金刚石窗对光束的影响

透射率随波长变化的波动小，对实验光谱不会产生较大影响。将 CVD金刚石加工成有楔角的形状(图3)能很好抑制透射率变化[10,11]。

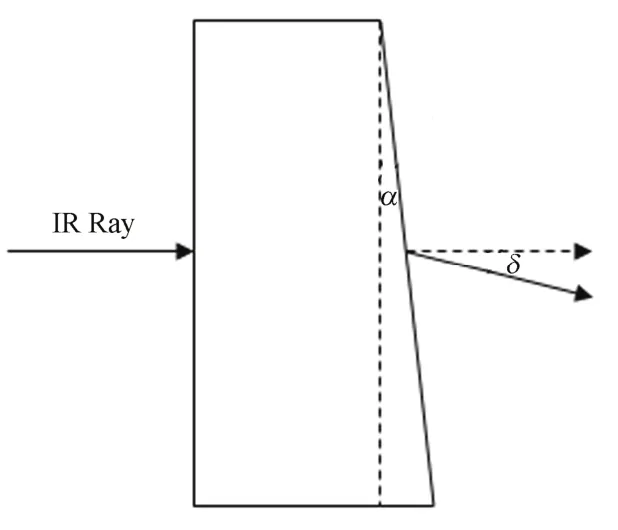
图3 有楔角的金刚石示意图Fig.3 A CVD diamond window with wedged angle.

用d(x,y)描述有楔角的CVD金刚石厚度变化，则式(8)变为：

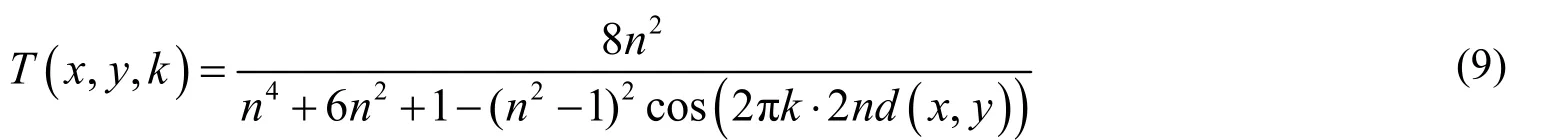
T(x,y,k)表示波数为k时点(x,y)处的透射率，于是总的透射率为：

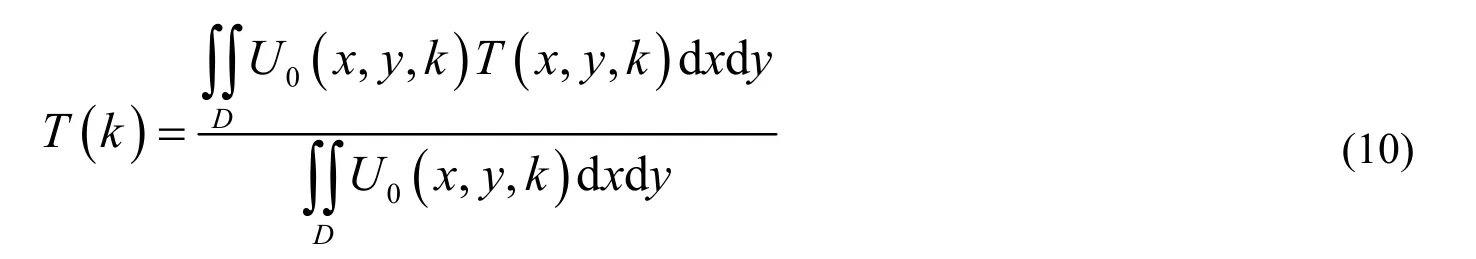
图 4是均匀光照下(即U0(x,y,k)为常数)不同楔角时 CVD金刚石透射率随波数的变化曲线，随着楔角引入，透射率变化幅度变得平稳，楔角越大，效果越好，越接近平均值。图5为红外和近红外波段透射率随波数变化曲线，可见周期性变化幅度很小(仅0.2%)。因此，有楔角的金刚石对透射率的影响主要集中在远红外波段。

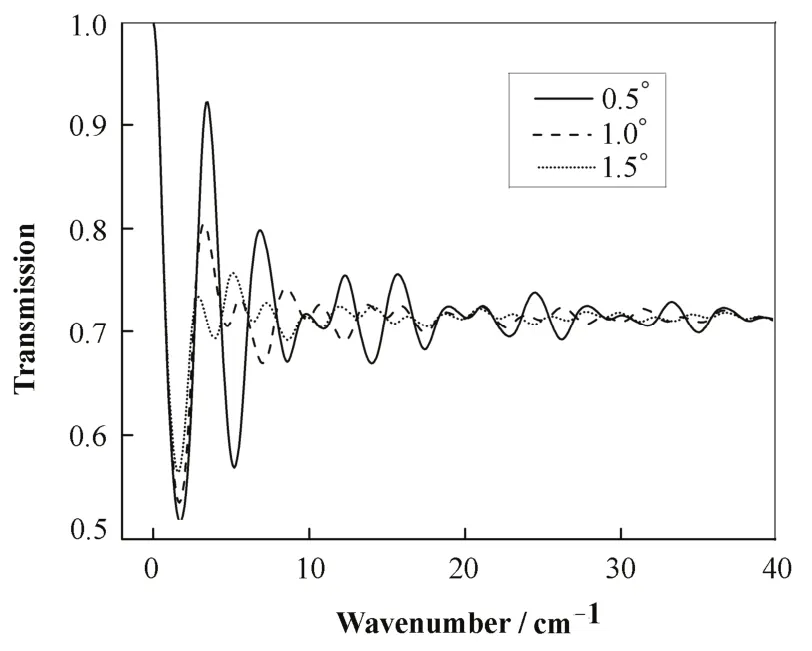
图4 楔角为0.5°, 1°和1.5°下CVD金刚石透射率随波数的变化曲线Fig.4 Transmission vs wavenumber for a CVD diamond window with wedged angles of 0.5°, 1° and 1.5°.

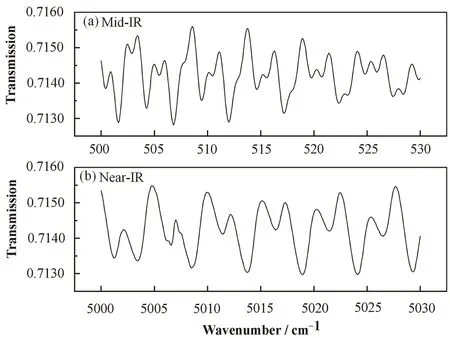
图5 中红外(a)和近红外(b)波段，透射率随波数的变化曲线Fig.5 Transmission as a function of wavenumber in MIR(a) and NIR(b).

3 上海光源红外光束线模拟光斑形状及其对透射率的影响

以上计算均基于均匀光照的情况，然而实际光束是不均匀的，故须结合实际的光斑计算。基于设计参数，用SRW软件[12]模拟了上海光源BL01B红外光束在 CVD金刚石处的光斑形状，计算透射率变化，以便真实模拟CVD金刚石对透射率的影响。

图6是用SRW模拟出的光斑形状，由于采用边缘辐射，光束形状与传统弯铁光源的光束形状明显不同。图7为波数在10-40 cm–1时透射率的变化，可见增大楔角可明显降低红外透射率的波动。楔角为0.5°时，透射率变化最大位置在11.5 cm–1附近，相对于平均值变化了 9.2%；楔角为 1°时，仅为2.7%(相对于平均值0.714)。

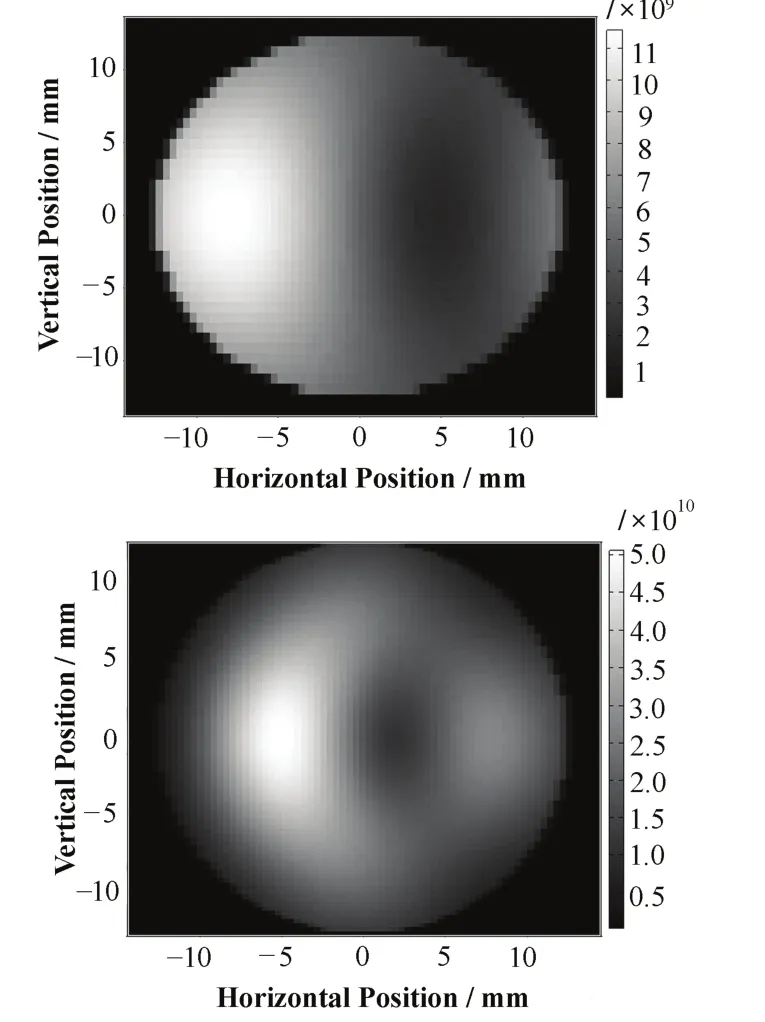
图6 SRW模拟得到的在CVD金刚石处的光斑形状，波数分别在 20 cm–1(上)和 40 cm–1(下)Fig.6 Profile at CVD diamond calculated by SRW with wavenumbers of 20 cm–1 (above) and 40 cm–1 (below).

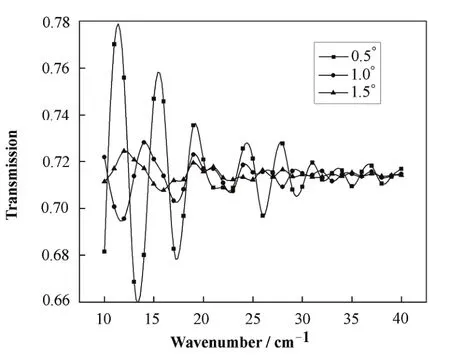
图7 用模拟光斑计算得到的透射率随波数的变化曲线Fig.7 Transmission as a function of wavenumber calculated by simulated spots.

图6还表明，在远红外波段，光斑形状并非圆对称，而是在水平方向对称。有楔角的金刚石厚度会变化，不同安装角度(金刚石厚度变化幅度最大方向和水平方向的夹角)对透射率有一定影响，故需研究不同安装角度下金刚石窗对红外透射率的影响。

图8是楔角为1°时不同安装角度的红外透射率变化，并用标准差评价透射率的变化幅度，可见安装角度为90°时，透射率变化幅度最小。

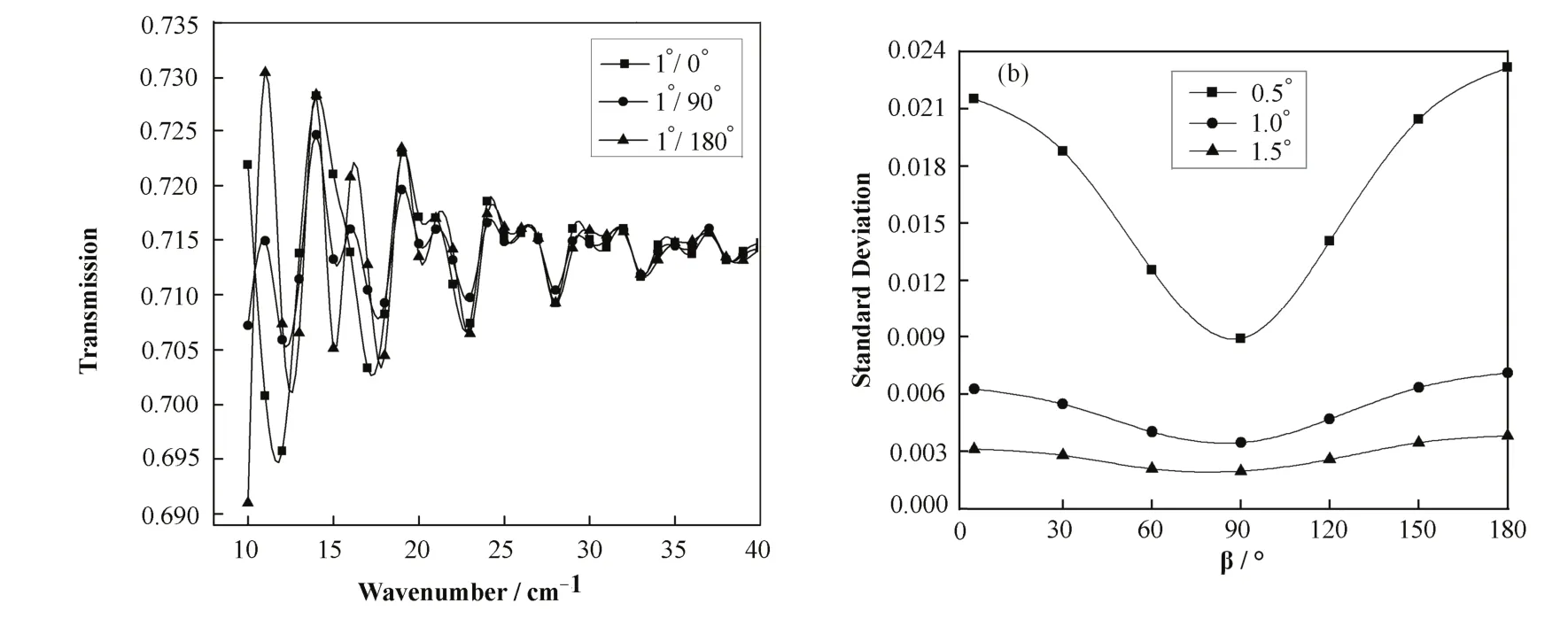
图8 楔角为1°，不同安装角度下透射率随波数的变化(a)和标准差随安装角度的变化(b)Fig.8 Transmission vs wavenumber (a) and standard deviation vs installation angle (b)at different installation angles, with a wedged angle of 1°.

由式(8)得到透射率的调制周期为P(cm–1) =1/(2nd), 其中，n是CVD折射率，d是CVD金刚石窗的厚度(对于有楔角的金刚石是平均厚度)，所以厚度主要影响透射率的变化周期。对于图2的金刚石调制周期约为3.5 cm–1。CVD越厚，吸收就越大，会降低通量，因此只要厚度能达到所需的抗断强度即可，6 mm的CVD金刚石即能满足该条件。

楔角使金刚石厚度发生变化，楔角越大，厚度变化越大，透射率变化越小；同样，金刚石直径越大，对于一定的楔角，厚度变化就越大，效果也越好。此结果是建立在光斑足够大前提下，一般只要金刚石尺寸和光斑大小相匹配即可。

4 结语

本文讨论了CVD金刚石对红外光束的影响，主要体现在金刚石前后面的多重反射现象使透射率周期性变化。通过把 CVD金刚石加工成楔型，能很好抑制透射率过大变化，使其平稳。用上海光源红外线站的参数，通过SRW模拟出CVD金刚石处的光斑形状，计算出透射率变化。结果表明，在有楔角情况下，透射率的大幅度变化主要集中在远红外波段，当楔角为1°时，最大透射率变化为2.7%，是较好的结果；当安装角度是 90°时，透射率变化幅度比其他情况更小；在厚度和尺寸的选择上，除了满足抗断强度外，CVD尺寸需和光斑大小匹配。

1 Jennifer M B, Michael W G, Jon R S,et al.Application of transient infrared and near infrared spectroscopy to transition metal complex excited states and intermediates[J]. Coord Chem Rev, 2007, 251: 492–514

2 Petibois C, Cazorla G, Cassaigne A. Application of FT-IR spectrometry to determine the global metabolic adaptations to physical conditioning in sportsmen[J]. Appl Spectrosc, 2002, 56: 1259–1265

3 Wayne R M, Michael C M, Carol J H,et al. First infrared beamline at the ALS design, construction, and initial commissioning[R]. Proc National Acad Sci, 1997

4 Lobo R P, Laveigne J D, Reitze D H,et al. Performance of new infrared beamline U12IR at the National Synchrotron Light Source[J]. Rev Sci Instrum, 1999,70(7): 2899–2904

5 Kimura H, Moriwaki T, Takahashi S,et al.Infrared beamline BL43IR at SPring-8 design and commissionning[J]. Nucl Instrum Methods Phys Res A, 2001, 467:441–444

6 Pascale R, Mathieu R, QI Zeming,et al. The AILES infrared beamline on the third generation synchrotron radiation facility SOLEIL[J]. Infrared Phys Technol, 2006,49(1–2): 139–146

7 May T E. Infrared facility at the Canadian light source[J].Infrared Phys Technol, 2004, 45: 383–387

8 戚泽明, 李承祥, 洪义麟, 等. 同步辐射红外光源和NSRL红外光束线站[J]. 核技术, 2008, 31(12): 881–885 QI Zeming, LI Chengxiang, HONG Yilin,et al.Infrared synchrotron radiation and the NSRL infrared beamline[J].Nucl Tech, 2008, 31(12): 881–885

9 Sara C, Bernhard S, Peter S,et al. Far-infrared transition and diffraction radiation. Part II: The THz beamline at the VUV-FEL linac[R]. TESLA-FEL 2006: 04

10 Paolo D, Alessandro N, Daniele C,et al. Infrared properties of chemical-vapor deposition polycrystalline diamond windows[J]. Appl Optics, 1998, 37(24): 5731–5736

11 Sussmann R S, Pickles C S J, Brandon J R,et al.CVD diamond windows for infrared synchrotron applications[J].Il Nuovo Cimento, 1998, 20(4): 503–525

12 Chubar O, Susini J, Cotte M,et al. Simulation and optimization of synchrotron infrared micro-spectroscopic beamlines using wave optics computation: ESRF and SOLEIL's cases[J]. AIP Conf Proc, 2007, 879: 607–610