石英β剂量的蒙特卡罗模拟

陈少文 黄 龙 朱德海 唐 强 刘小伟

1 (东莞理工学院 东莞 523808)

2 (中山大学物理科学与技术学院 广州 510275)

再生照射是TL或OSL测定年代方法中的必要步骤，对样品吸收剂量的精确测量是影响年代测定的重要因素。90Sr-90Y β源常用于测年实验室的再生照射，其母核90Sr(t1/2= 28.8 a)的β射线最大能量为0.55 MeV，子核90Y(t1/2= 64 h)的β射线最大能量为2.28 MeV。β粒子能量不一，在样品中射程也不同，β射线样品中的吸收、衰减和反散射等各种效应都对剂量有影响，颗粒的大小、样品厚度等也会影响源的标定剂量。对较大颗粒或薄片样品，受到的辐照不能全部视为均匀。由于无法将石英样品制成厚约10 μm薄片，不少作者用铝替代石英进行β源辐照，研究吸收剂量的深度分布[1–5]。但是，铝与石英的成分、密度、质量能量吸收系数及质量碰撞阻止本领等参数不一样[6]，用铝所得结果会有异于石英。

Monte Carlo模拟可用于石英中的吸收剂量研究[7]。本文用蒙特卡罗方法对用β源辐照时不同厚度样品片和不同大小石英单颗粒中的吸收剂量进行模拟，研究样品中吸收剂量随深度分布的规律，讨论薄片样品厚度以及颗粒大小对吸收剂量的影响。

1 材料和方法

图 1为模拟模型示意图，90Sr-90Y放射性化合物镀在Φ12 mm×1 mm 的银圆片上，源活度 1.5 GBq，活性面厚度约0.2 mm，表面覆盖有0.1 mm厚的银屏蔽层，源与样品的距离为16 mm。容器内为1个大气压的氮气，整个装置用铅屏蔽。

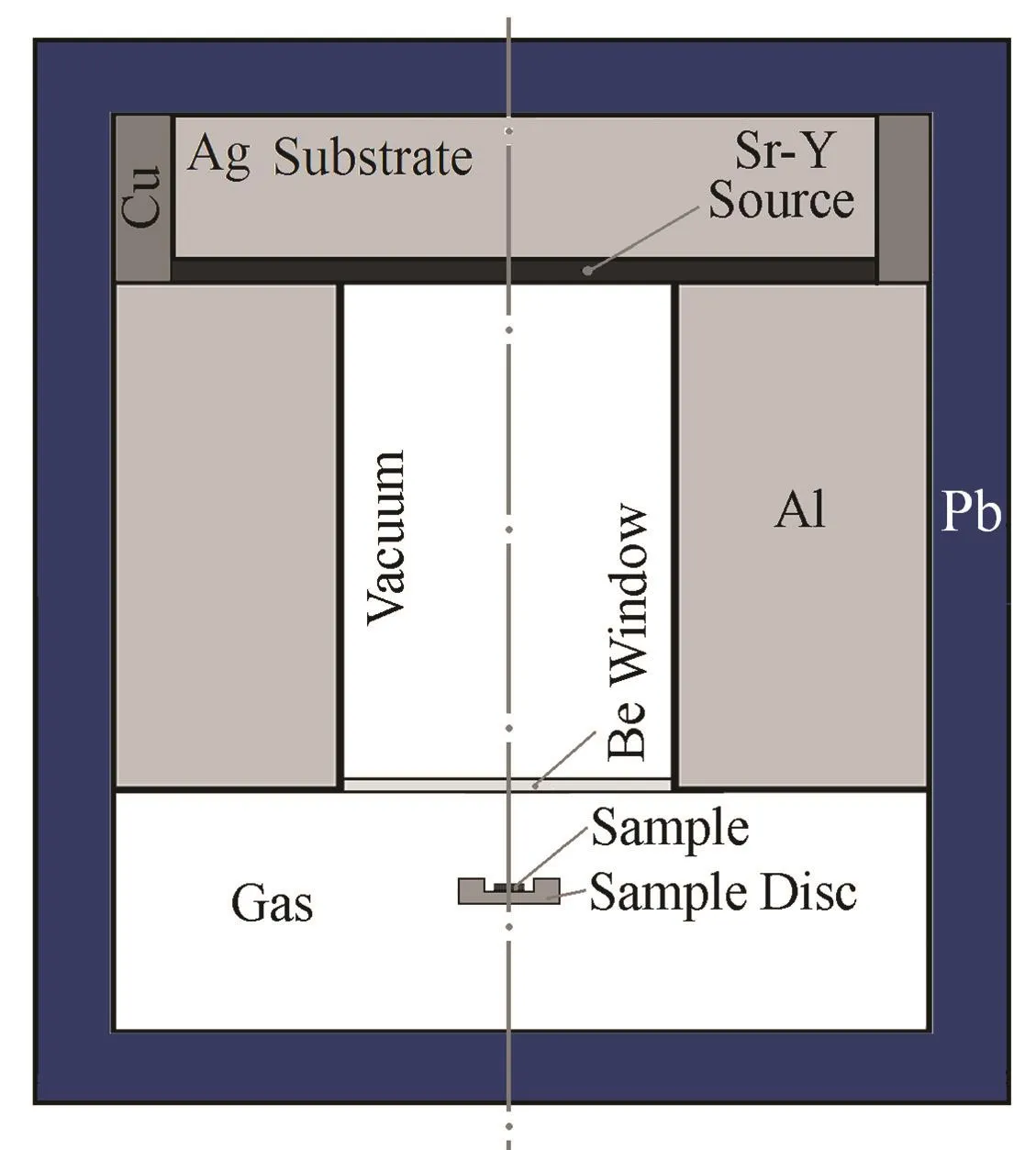
图1 模拟示意图Fig.1 Schematic diagram of the simulation.

样品盘为铝盘，直径0.97 cm[8,9]。圆柱形薄片样品直径为 0.97 cm，厚度 10–500 μm，置于厚度0.7 mm的样品盘上。模拟单颗粒时，厚度1 mm的样品盘中央留出直径和深度均为300 μm的样品小孔，单颗粒圆柱形样品直径和高度相同，大小为60–300 μm，置于小孔中。石英和铝的密度分别为2.65g/cm3和 2.70g/cm3。

模拟时90Sr-90Y 源的β射线谱采用EGSnrc系统[10]的sr90y90.spectrum，β射线能量0 –2.5 MeV，分成 50个区间。采用 EGSnrc系统[10]的程序DOSRZnrc进行吸收剂量的计算，光子和电子的反应截面由 PEGS4代码产生。电子的截止能量设为0.521 MeV，光子为 1 keV。除了方差减少技术中Electron Range Rejection的ESAVEIN设为2.0 MeV外，其它输运参数均为缺省配置。

模拟时使用 Intel(R) Core(TM) i5 CPU M430@2.27GHz 处理器，win7操作系统，在吸收剂量计算误差～1%情况下，对样品片模拟 1×108个入射粒子约需5.3 h的CPU时间，对应标准辐照源活度，模拟1.5 G的入射粒子过程需约80 h的CPU时间。对于厚度为300 μm样品片，模拟得到的剂量率约为0.064 Gy/s，与普通测年实验室中使用的剂量率基本一致。对单颗粒模拟则需更多的入射粒子数和很长的计算时间，模拟大小为60 μm的单颗粒，要达到吸收剂量的计算误差约为 1%，入射粒子数为8.4×109个，需要380 h的CPU时间。

2 结果和讨论

2.1 吸收剂量随深度的分布

图2给出了厚度500 μm的石英和铝样品中的吸收剂量随深度分布的曲线，图中相对剂量归一到第一层(10 μm)的剂量，误差线(一个标准差)的大小约为数据标记的高度。

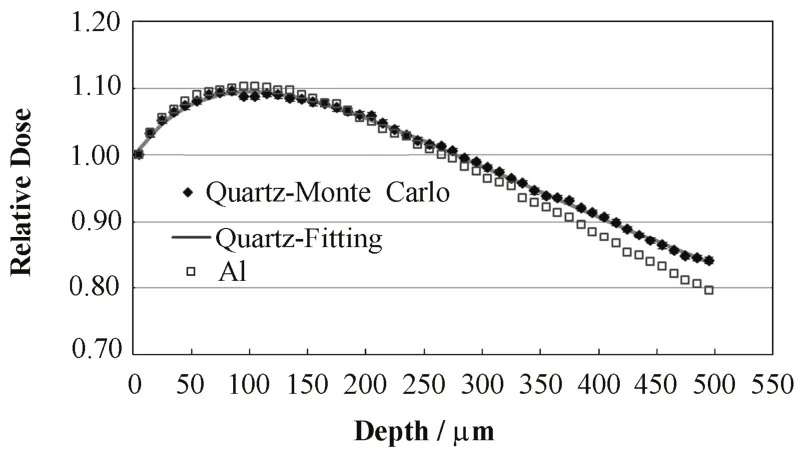
图2 石英和Al样品中吸收剂量随深度的分布Fig.2 Depth-dose distribution of the absorbed dose to quartz and Al sample.

由图 2，石英和铝样品中的相对剂量并非完全一样。由于相对剂量归一到第一层(10 μm)的剂量，当深度小于250 μm时，石英和铝样品中的相对剂量相差不大，差异小于1%；但随着深度的增加，石英和铝样品中相对剂量的差异逐渐变大，铝中的相对剂量比石英中的小，当深度为250–350 μm时差异约为1%–2%，深度为350–450 μm时差异约为3%–4%，深度接近 500 μm 时差异约为 5%。根据NIST数据[6]，当电子的动能为0.1–3 MeV时，铝中的质量碰撞阻止本领比石英中的小，比值约为0.94–0.96。铝中吸收剂量的增加比石英中的慢，所以，随着深度的增加铝中的相对剂量比石英中的小。

图2还表明，石英和铝样品中的β剂量随深度的分布并不均匀。一开始随深度增加，相对剂量也增加，在约100 μm处达最大值，比表面剂量高约10%；此后的剂量逐渐减少，在500 μm处石英和铝的相对剂量约为表面的84%和80%，与文献[7]模拟结果相一致，与文献[3–5]的实验结果有可比性，但与文献[1,2]的实验结果差异较大。文献[1,2]实验所用的 β源及辐照条件与本文不一样，故其 200 μm处剂量为最大值，比表面剂量高约20%，而在500 μm 处的相对剂量跟表面的值相差不大。文献[3–5]实验除用铝片作辐照样品外，其他实验条件跟本文模拟的基本相似，其剂量最大值比表面剂量高约10%，与本文结果一致。但文献[3–5]的剂量最大值出现在40 μm处，500 μm处剂量约为表面的74%，这与本文的结果有差异。

β剂量随深度分布是β剂量积累和衰减效应竞争的结果，最初，积累效应占优势，吸收剂量逐渐增加至最大值，之后积累效应饱和，衰减效应开始占优势，剂量逐渐减少。同时考虑积累和衰减效应，根据经验公式，深度x处的相对剂量为[3–5]：

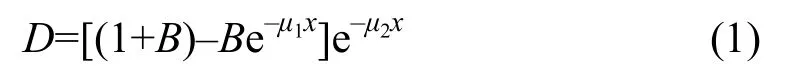
其中，B为饱和常数，μ1为衰减因子，μ2为积累因子。用Matlab的cftool工具箱对石英中模拟得到的结果进行双指数拟合，可得B=0.280，μ1=0.0118271，μ2=0.0008529。代入式(1)计算石英样品中不同深度处的相对剂量，与模拟结果相差<1%。

2.2 样品厚度对吸收剂量的影响

由于β剂量在薄片样品中随深度变化，薄片样品中的β吸收剂量仅用平均剂量表示。图3给出直径为9.7 mm的石英薄片样品中厚度对吸收剂量的影响，相对剂量归一到厚度为10 μm时样品的剂量，图中误差线表示一个标准差大小。

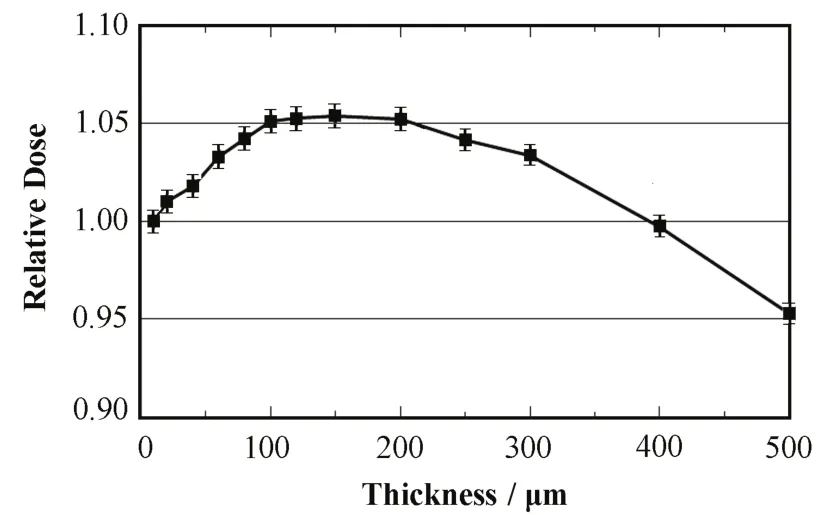
图3 石英薄片样品厚度对吸收剂量的影响Fig.3 Effect of thickness of the quartz slice samples on the absorbed dose.

由图3，厚度较小时，相对剂量随厚度增加，约为100 μm时达最大值，然后逐渐减少。厚度为10–500 μm的石英薄片样品，相对剂量的差异可达10%。石英薄片样品厚度为100、200、300、400、500 μm时，相对剂量分别为1.051、1.052、1.034、0.997、0.953。文献[3–5]用铝得到的实验结果分别为1.047、1.036、1.008、0.965、0.932，两组结果的差异为1%–3%。

同样，吸收剂量与样品厚度有关，可归因于 β剂量积累和衰减效应竞争的结果，也与β射线反散射的结果有关。由图3可得厚度为10–500 μm石英薄片样品中的平均β吸收剂量。

2.3 单颗粒大小对吸收剂量的影响

图4为石英单颗粒大小对吸收剂量影响的模拟结果，石英颗粒大小为60–300 μm，相对剂量归一到大小(直径)为 300 μm时的颗粒，图中误差线为一个标准差大小。

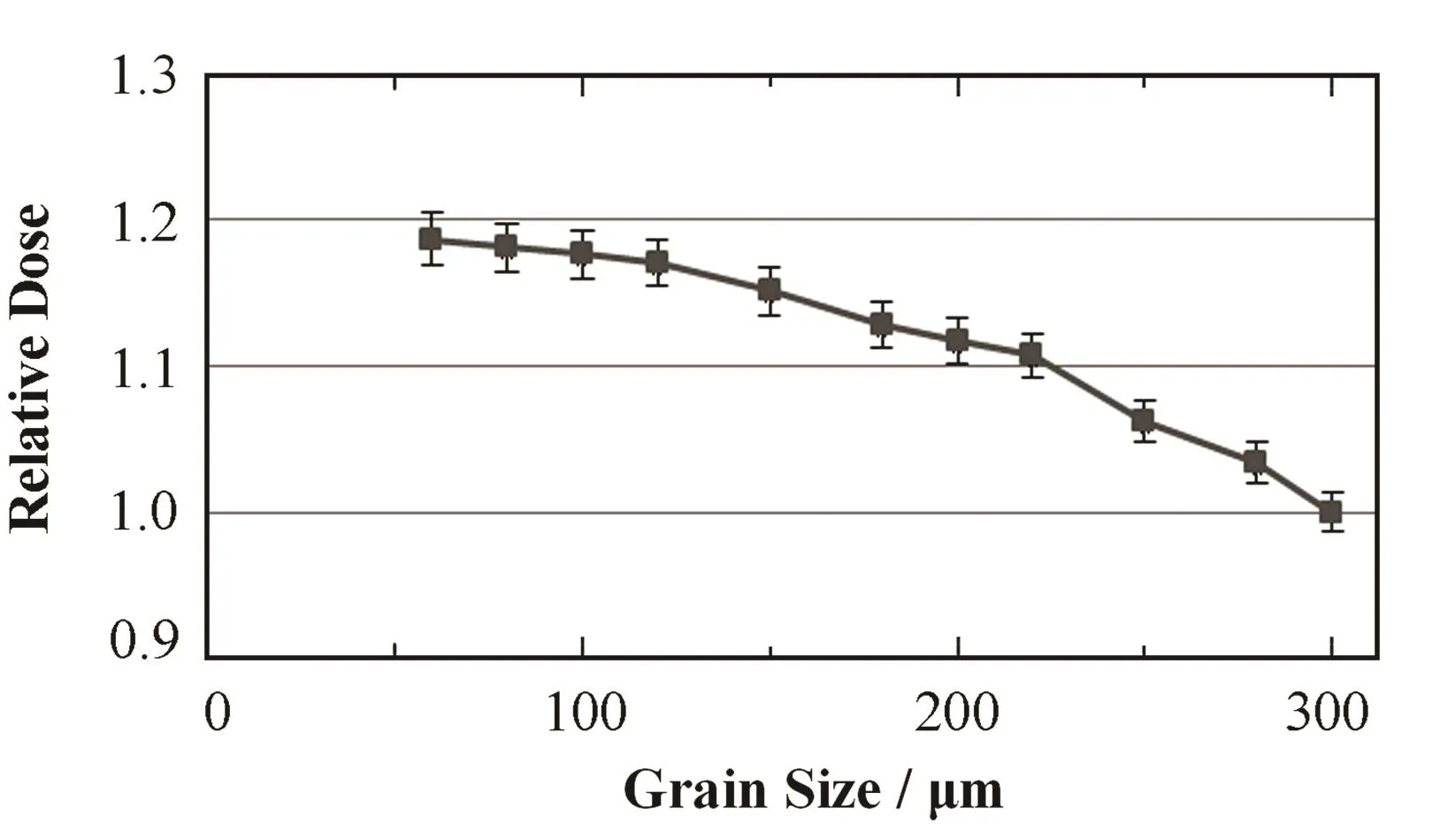
图4 石英颗粒大小对吸收剂量的影响Fig.4 Effect of the quartz grain size on the absorbed dose.

图4 表明，吸收剂量明显与颗粒大小有关，相对剂量随石英颗粒的变小而增大。颗粒直径为 60 μm 时的相对剂量为 1.1872±0.0176，比直径为 300 μm时的相对剂量增加约 19%。使用单颗粒测量时颗粒的最佳大小为 180–250 μm[8,9]，此范围相对剂量在 1.0623±0.0141与 1.1277±0.0157间，约有 6%的差异。由于在较小颗粒中由反散射得到吸收剂量的份额较大，颗粒大小不同，吸收剂量不一样，在使用单颗粒测量时应尽量筛选大小一致的颗粒。

3 结语

用蒙特卡罗模拟程序EGSnrc /DOSRZnrc对不同厚度样品片和不同大小石英单颗粒中的吸收剂量进行模拟，结果表明：(1) 石英和铝样品中的吸收剂量并不完全一样，随着深度的增加，石英和铝样品中的相对剂量差异逐渐变大，铝中的相对剂量比石英中的小；(2) 薄片样品中的 β剂量随深度分布并不均匀，一开始相对剂量随深度增加，深度为100 μm处达到最大值，比表面的值约高 10%，然后相对剂量逐渐减少；(3) 吸收剂量与薄片样品的厚度有关，厚度为10–500 μm的石英薄片样品，相对剂量的最大差异可达10%，厚度约为100 μm时吸收剂量有最大值；(4) 吸收剂量与石英单颗粒的大小有关，相对剂量随颗粒的变小而增大，大小在60–300 μm的颗粒，吸收剂量最大的差异约有19%。总之，吸收剂量与样品片厚度和石英单颗粒大小有关，在测定年代过程中这些因素需要加以考虑。

1 Wintle A G, Murray A S. Thermoluminescence dating:Re-assessment of the fine grain dose-rate[J]. Archaeometry, 1977, 19(1): 95–98

2 Aitken M J. Thermoluminescence dating[M]. London:Academic Press, 1985

3 王维达, 周智新, 夏君定, 等. 瓷片中 β剂量的积累和衰减研究[J]. 核技术, 1995, 18(8): 454–457 WANG Weida, ZHOU Zhixin, XIA Junding,et al.Build-up and attenuation of beta dose within a porcelain slice[J].Nucl Tech, 1995, 18(8): 454–457

4 WANG Weida. Evaluation for the paleodose in thermoluminescence dating of porcelain[J]. Sci China Ser E-Tech Sci, 2008, 51(3): 260–267

5 王维达. 瓷器热释光断代中 β平均剂量计算方法研究[J]. 文物保护与考古科学, 2005, 17(1): 1–4 WANG Weida. Calculation of average beta dose in porcelain irradiated by a90Sr-90Y source[J]. Sci Conserv Archaeol, 2005, 17(1): 1–4

6 NIST. Physics Databases, NIST Scientific and Technical Databases[OL]. http://www.nist.gov/srd/physics.htm, Last Update: Dec 2008

7 CHEN S W, LIU X W, ZHANG C X,et al. The Monte Carlo simulation of the absorbed dose in quartz[J]. Radiat Meas, 2009, 44(5–6): 626–628

8 Thomsen K J. Optically stimulated luminescence techniques in retrospective dosimetry using single grains of quartz extracted from unheated materials[D]. Roskilde,Denmark, Risø National Laboratory, 2004

9 Risø TUD. Guide to “The Risø Single grain laser OSL system”[R]. Risø National Laboratory, 2009

10 Kawrakow I, Rogers D W O. The EGSnrc Code System:Monte Carlo simulation of electron and photon transport[R]. NRCC Technical Report PIRS-701, 2003