多幅图像中值法在滤除噪声中的应用
孙永生,刘大健,秦 蒙
(中国计量学院a.信息工程学院;b.现代科技学院,浙江 杭州 310018)
责任编辑:魏雨博
图像滤波就是抑制图像中的噪声,减少噪声对图像的影响,提高图像信噪比。图像滤波的方法有很多种,但总结起来主要是线性和非线性滤波器两大类[1]。传统的滤波方法有邻域平均法、中值滤波法和多图像平均法[2-5]等。邻域平均法在降低噪声的同时也使图像出现模糊,特别是在边缘和细节处[6];中值滤波法容易去除孤立点、线的噪声,同时保持图像的边缘,但对高斯噪声无能为力[7];多图像平均法虽然能很好地去除噪声并明显优于中值和均值算法,但可能会丢失部分边界纹理信息[8]。
针对上述的滤波算法本文也提出了一种滤波算法,即多幅图像中值法,该方法首先要对同一场景多次提取图像,然后将这些图像的中值作为该图像的输出值,实验表明该算法简单有效,不仅能最大程度地滤除椒盐噪声,而且对高斯噪声滤波效果较好。
1 同场景多幅图像的降噪
1.1 椒盐噪声
图像在获取和传输中,数字图像经常受到脉冲噪声的影响[9],中值滤波器对消除脉冲噪声非常的有效 。脉冲噪声可以是正的(盐点),同样也可以是负的(胡椒点),故这种噪声也可称为“椒盐噪声”。
椒盐噪声一般情况下总是表现为图像局部区域的最大值或最小值,受污染的像素位置是随机分布的,且正负噪声点出现的概率几乎相同。若需要对图像进行处理,如图像分割、目标识别和边缘检测等,则需要降低噪声对图像的影响。令Yij表示图像Y在位置(i,j)的真实灰度值,Xij表示受椒盐噪声污染的图像Y在位置(i,j)点的灰度值,则椒盐噪声的PDF可表示为[10]
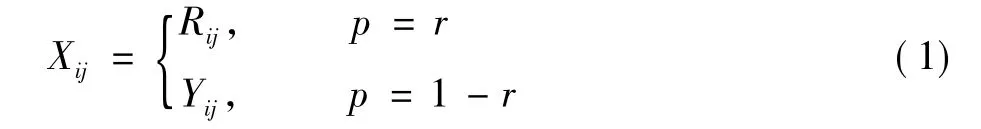
式中:Rij∈[0,255]是一个随机的数字;r是椒盐噪声概率。
1.2 高斯噪声
所谓高斯噪声是指它的概率密度函数服从高斯分布(即正态分布)的一类噪声。一个高斯随机变量x的PDF可表示为

式中:x表示图像灰度值;m表示x的平均值或期望值;σ表示x的标准差,σ2称为x的方差。高斯函数的曲线如图1所示,当x服从式(2)的分布时,其值有70% 落在[(m-σ),(m+σ)]范围内,且有95% 落在区间[(m -2σ),(m+2σ)]内。

图1 高斯函数图
当m=0时,式(2)则变为

图1中的高斯函数图将向左移动m个单位,成为一个关于p(x)的轴对称偶函数。
1.3 多幅图像中值滤波
在多幅图像中值滤波时,首先要提取若干同场景的图像,这里假设同场景图像的个数为N,其中第n幅图像g 在点 (i,j) 处的灰度值表示为 g(i,j,n),1 ≤ n ≤ N ,则同场景多幅图像中值滤波后点(i,j)的灰度值f(i,j)为

式中:median{·}表示中值操作。多幅图像中值滤波的算法流程图如图2所示。
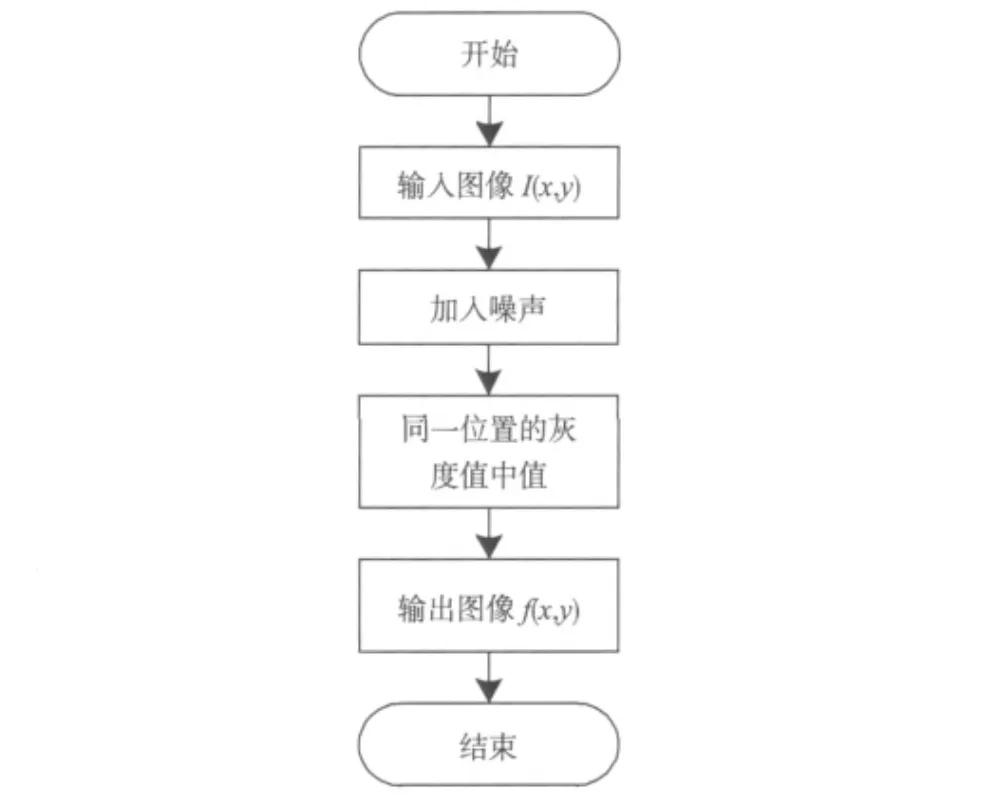
图2 算法流程图
2 实验结果分析
为验证该算法的有效性,用256×256,256级Lena灰度图像,将本文算法与中值滤波、均值滤波、多幅均值滤波进行比较。对各种滤波方法的优劣采用主观评价和客观评价标准相结合,客观评价标准采用均方误差PMSE和峰值信噪比 PSNR[11-12]。
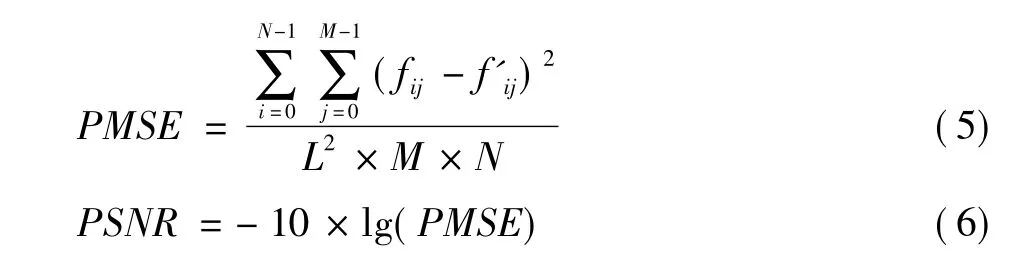
式中:N,M分别是x方向、y方向上图像像素点的个数;fij和f'ij分别是原始图像和加噪声后图像在点(i,j)上的灰度值;L是图像中灰度取值的范围,对8 bit的灰度图像而言L=255。
为了验证该算法的有效性,准备了3组实验,分别用MATLAB实现。
第1组实验对标准的Lena图像进行分析比较,首先对该图像添加密度为0.1的椒盐噪声,然后将该被污染的图像作为输入,对其分别利用不同方法进行滤波。中值和均值滤波的窗口大小为3×3,多幅中值法和多幅均值法的输入是100幅含有该密度的椒盐噪声图像,表1为利用不同算法对该图像滤波的客观评价指标。

表1 各算法滤除椒盐噪声的指标比较
图3为不同的滤波算法对含有椒盐噪声图像的滤波效果图。

图3 各算法滤除椒盐噪声后的图像
在表1中可以清楚地看到多幅中值滤波法的峰值信噪比最高、均方误差最小,均值滤波法的峰值信噪比最低、均方误差最高,所以在客观上多幅中值滤波的效果最好。结合图3的滤波效果图可知,多幅中值滤波后的图像接近原图像,效果明显好于其他算法。
第2组实验进一步比较该算法在其他噪声中的滤波性能,这次对标准的Lena图像添加均值为0.1,方差为0.05的高斯噪声,然后比较多幅中值滤波算法和其他算法的优异性。中值和均值滤波算法还是采用3×3的模板降噪,多幅中值滤波和多幅均值滤波图像个数仍为100幅。
首先采用客观评价标准对这几种滤波算法进行分析比较,表2是对加入该噪声后的图像利用不同算法滤波的客观评价指标。
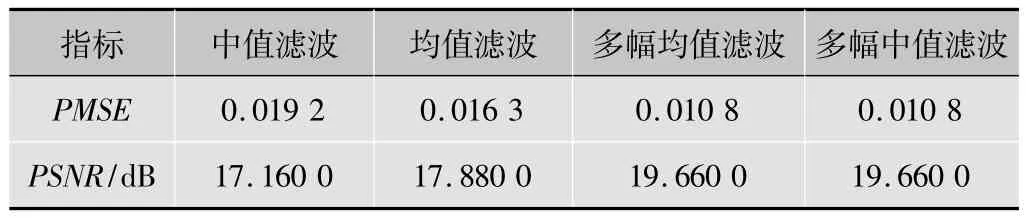
表2 各算法滤除高斯噪声的指标比较
然后再用主观评价标准对上述的滤波算法的滤波效果进行对比,见图4。

图4 各算法滤除高斯噪声后的图像
最后由主观评价标准和客观评价标准可知,中值和均值滤波的效果几乎相同,在滤波后的图像中可以明显含有噪声,即滤波的效果不是很好;而采用多幅均值和多幅中值滤波法则不存在上述问题,表2则显示这两种算法滤波效果几乎相同,但图4显示多幅中值滤波的图像的灰度对比度较高。
第3组实验是在标准的Lena图像中加入第1组、第2组的噪声,中值和均值滤波算法仍采用3×3的模板降噪,多幅中值滤波和多幅均值滤波图像个数仍为100幅。
用客观评价标准对此噪声图像滤波效果进行评价,表3为对加入密度为0.1的椒盐噪声和均值为0.1,方差为0.05的高斯噪声的各算法滤波的客观评价指标。
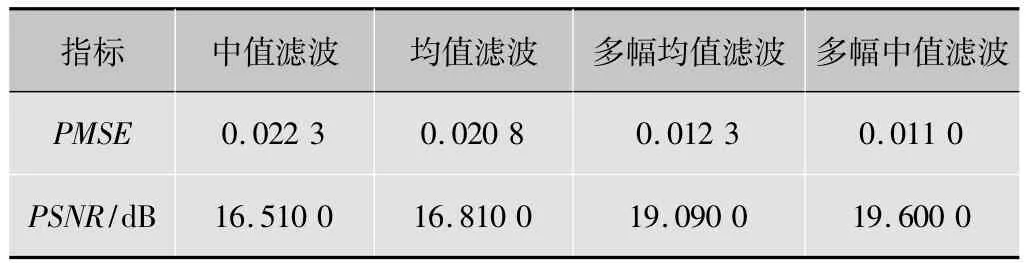
表3 各算法滤除椒盐和高斯噪声的指标比较
下图就是这几种滤波算法滤波后的图像比较,结果如图5所示。

图5 各算法滤除椒盐和高斯噪声后的图像
当图像中同时夹杂有高斯噪声和椒盐噪声时,无论是客观评价还是主观评价多幅中值滤波算法的滤波效果都是最好的,它比传统的中值和均值算法能更好地滤除噪声。相对于多幅均值滤波法,它的峰值信噪比略高,并且滤波后的图像也优于多幅均值滤波后的图像。
3 结论
本文论述了多幅中值算法在图像滤波上的作用,并且将它和传统的几种滤波算法进行了比较。在含有椒盐噪声或高斯噪声或两者兼有的情况下,该算法明显优于传统算法,能够较好地达到图像降噪的目的,特别是椒盐噪声。在含有高斯噪声的条件下虽然在保护细节方面优于其他算法,但仍然存丢失部分边界纹理信息,并且该算法忽略了多次摄取图像时摄像头的抖动,这在一定程度上限制了它的应用。
[1]CASTLEMAN K R.Digital image processing[M].北京:清华大学出版社,1998.
[2]任玲.数字图像的平滑技术[J].电脑编程技巧与维护,2011,(14):115-116.
[3]李世进.数字图像的平滑处理[J].湖南科技学院学报,2008,29(12):23-24.
[4]黄涛.数字图像的平滑[J].韶关学院学报,2004,25(6):25-29.
[5]TUKEY J W.Exploratory data analysis[M].MA:Addison Wesley and Sons,Inc.,1994.
[6]张永超,程佳,梁国伟,等.用于工业现场的摄像机标定方法研究[J].中国计量学院学报,2011,22(3):246-250.
[7]孙海英,李锋,商慧亮.改进的变分自适应中值滤波算法[J].电子与信息学报,2011,33(7):1743-1747.
[8]马艳娥,陈思,陈娟,等.基于多幅图像平均法对数字图像降噪的研究[J].电子测量,2011(6):1-3.
[9]DONG Y Q,CHAN R H,XU S F.A detection statistic for random-valued impulse noise[J].IEEE Trans.Image Processing,2007,16(4):1112-1120.
[10]ZHANG JianJun,WANG Qin.An efficient median filter based method for removing random-valued impulse noise[C]//Proc.International Conference on Audio,Language and Image Processing(ICALIP 2008).Shanghai:Shanghai University Press,2008:918-922.
[11]李连胜,陈晚华.基于MATLAB的数字图像质量评价[J].湖南科技学院学报,2005,26(5):176-177.
[12]LIN T C.A new adaptive center weighted median filter for suppressing impulsive noise in images[J].Information Sciences,2007,177(4):1073-1087.

