古汉语双字词自动获取方法的比较与分析

段 磊，韩 芳，宋继华

(北京师范大学 计算机科学与技术学院,北京 100875)

1 概述

在汉语中，字和词不是同一个概念。词是语言中可以独立运用的最小表意单位，而字是词的记录符号[1]。

与现代汉语中双字词和多字词居多的情况不同，在古汉语中，多数为单字词，少数为多字词，因而增加了多字词获取的难度。但由于古汉语句式简单、单句字数少，反而减少了对多字词获取结果的干扰。所以将词汇获取的统计模型应用于古汉语，可以更加客观地评价各种获取方法的性能。对古代汉语词汇的自动获取方法进行研究，其成果不但将对古汉语词典编撰等古籍的信息化处理应用起到不可忽视的作用，同时也会促进古汉语语法研究与现代汉语语法研究的结合，推动现代汉语语法研究的深入展开。

我国历史悠久，文化遗产丰富，用文言记录的典章制度及史料，用文言撰写的文学作品，多到不可计数。由于时间跨度大(上下三千多年)，不同时代，不同体裁的文言作品，其语言特点有很大差异。而最能反映古汉语原貌的，莫过于先秦两汉的作品[1]。由我国西汉著名史学家司马迁撰写的纪传体史书——《史记》，是先秦两汉文学作品中最具有代表性的典籍之一，被誉为“史家之绝唱，无韵之《离骚》”。

已有相关的统计自然语言处理专著[2]及论文[3]曾对搭配获取方法进行过阐述。在自然语言处理领域中，“搭配”一般指两个或多个连续的词序列构成的某种习惯性的表达，是词与词的关系[4]。本文针对古汉语双字词的自动获取问题，通过考察字与字的关系，以《史记》全文语料库为例，分别应用了基于频率、互信息(包括点互信息、三次互信息)、假设检验(包括t检验，卡方检验，似然比)等获取搭配的统计方法对古汉语双字词进行获取，并将获取结果与人工标注结果进行了详细的比较，评价了各方法的优缺点及可靠性，为不同应用背景下的古汉语双字词自动获取提供了相应的解决方案，从而找到针对不同需求的古汉语双字词获取的有效方法。

2 双字词自动获取方法

2.1 N元组(N-gram)

一个n元组是指一个含n个相邻字的字串。由单字生成n元组的唯一条件是它们在文本中连续出现。以《史记》第一篇《本紀—五帝本紀》第一句为例：

黃帝者，少典之子，姓公孫，名曰軒轅。

从该句中抽取n元组，其结果为：

二元组： 黃帝、帝者、少典、典之、之子、姓公、公孫、名曰、曰軒、軒轅(10个)；

三元组： 黃帝者、少典之、典之子、姓公孫、名曰軒、曰軒轅(6个)；

四元组： 少典之子、名曰軒轅(2个)。

本文主要对古汉语中双字词的自动获取进行研究，所以只考虑二元组的情况： 将《史记》中出现的所有二元组作为双字词的候选集，利用统计方法进行双字词的自动获取。

2.2 频率(Frequency)

在语料库中寻找双字词的最简单的方法就是计数。如果某个二元组出现了很多次，那么这就是一个证据，说明此二元组中的两个字之间存在着某种联系。从形式上看，词是稳定的字的组合，字与字相邻共现的频率或概率能够较好的反映成词的可信度。因此在上下文中，二元组出现的次数越多，组成此二元组的两个字就越有可能构成一个词。基于频率信息的双字词获取方法以二元组出现的次数，即观察频率(Observed Frequency)为依据来进行计算。

2.3 互信息(MI)

对于双字词的获取，一种以信息论为根据的方法是互信息。互信息体现了汉字之间结合关系的紧密程度。当两个字的紧密程度高于某一个阈值时，便可认为这两个字可能构成了一个词。利用互信息进行双字词获取的方法还可以细分为两种： 点互信息和三次互信息。

2.3.1 点互信息(PMI)

在双字词抽取中，点互信息表示连续出现的两个字中，一个字的出现所提供的关于另一个字出现的信息量，其公式如式(1)所示：

其中，P(w1,w2)表示二元组(w1,w2)在语料中出现的概率；P(w1)，P(w2)分别表示汉字w1，w2在语料中各自出现的概率；C12表示二元组(w1,w2)在语料中出现的次数，C1，C2分别表示汉字w1，w2在语料中各自出现的次数，N表示语料库中二元组的总次数(下同)。点互信息值越高，w1和w2组成双字词的可能性越大，点互信息值越低，w1和w2之间存在搭配边界的可能性越大[5]。

点互信息的一个致命缺点在于，它不能很好地解决低频率事件，容易受到数据稀疏的影响。考虑一种极端情况： 某两个字的出现是完全互相依赖的(它们都是一起出现)，此时：

也就是说，在完全依赖的二元组中，两个字出现的次数减少时，他们的点互信息增加。

另一种极端情况： 某两个字的出现是完全独立的(一个字的出现不能给出关于另一个字出现的任何信息)，此时：

=log21=0

(3)

由此可见，点互信息是衡量独立性的一种很好的方法。接近0的点互信息值表明了两个字完全独立，而对于依赖性来说，点互信息值是由单独字的频率来决定的，在其他条件相等的情况下，由低频单字组成的二元组的点互信息值要大于高频单字组成的二元组的点互信息值。点互信息倾向于为低频二元组赋予较高的值。

2.3.2 三次互信息(MI3)

三次互信息是在点互信息的基础上提出的[6]，其公式如式(4)所示：

其中，各参数的意义与点互信息的公式相同，主要区别在于对C12取三次方，扩大两个字同现次数对于评价指数的影响，来增加高频事件与低频事件的差距，从而解决点互信息对低频事件赋予较高的值的问题。

2.4 假设检验(Hypothesis Test)

假设检验是数理统计学中根据一定假设条件由样本推断总体的一种方法，基本思想是先对某事做出某种假设，然后根据统计量的数值结果来判断所做的假设是否可信，从而肯定或否定这个假设[7]。本文所介绍的用于双字词获取的假设检验方法包括t检验法、卡方检验法、似然比。

2.4.1 t检验(t Test)

t检验用t分布理论来推断差异发生的概率，从而判定两个平均数的差异是否显著。其中，H0表示二元组的组成单字为独立无关的情况，H1表示二元组为双字词的情况。具体计算公式如式(5)所示：

所以，

t检验考虑了二元组的出现次数相对于其中每个字的出现频率的比例。如果二元组的出现频率接近于其中每个字，或某一个字的出现频率，那么它的t值就会较高[2]，以此来检验二元组是否为双字词。

2.4.2 卡方检验(Chi-square Test)

卡方检验是以卡方分布为基础的一种常用假设检验方法，用途很广，主要用于分类变量[8]。在应用卡方检验到双字词获取的过程中时，我们利用下面两个对立假设来解释二元组w1w2的出现频率。

假设H0： 行分类变量与列分类变量无关联

假设H1： 行分类变量与列分类变量有关联

卡方检验值计算了观测值和期望值之间的差别的总和，为：

其中Oij表示表单元(i,j)的观测值，Eij是在H0为真的情况下表单元(i,j)的理论数(期望值)，i为表中的行变量，j为表中的列变量。

在H0为真时，实际观察数与理论数之差Oij-Eij应该比较接近0。

通过计算边缘分布可以得到期望频度Eij的值，计算方法为： 将表中的频度值转换为比例值后按行和列计算总数。

表1 表明单字“诸”和“侯”出现次数之间的依赖关系的2×2列联表

卡方检验从理论上讲适用于各种大小的表，但是对于2×2形式的列联表格(表1)的表达形式相对简单。针对双字词的具体计算公式如式(9)所示：

(9)

2.4.3 似然比(Likelihood Ratios)

似然比是反映真实性的一种指标，属于同时反映灵敏度和特异度的复合指标。在应用似然比检验到双字词获取的过程中时，我们利用下面两个对立假设来解释二元组w1w2的出现频率。

假设H0：P(w2|w1)=P=P(w2|w1)

假设H1：P(w2|w1)P1 ≠P2=P(w2|w1)

假设H0是独立性假设的形式化，而假设H1则是非独立性假设的形式化。

使用最大似然估计的方法计算P,P1和P2，则得：

(10)

表2所示为如何计算似然比检验。

表2 似然比计算方法

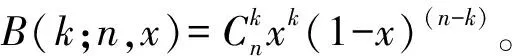
H0似然值：

L(H0)=B(C12;C1,P)B(C2-C12;N-C1,P)

(11)

H1似然值：

L(H1)=B(C12;C1,P1)B(C2-C12;N-C1,P2)

(12)

似然比λ的对数值：

3 结果分析

由于在不同的应用中对词汇的定义有着不同的理解，因此对词汇获取方法也存在着不同的评价标准，有专家进行人工评价的，也有利用已有词典进行评价的。本文利用中国台湾“中央研究院”发布的带有分词和词类标注信息的《史记》全文语料(后文简称“熟语料”)，从中得到所有双字词集合，即标注者认为的双字词集合，作为计算获取准确率的目标集合，从而评价双字词获取方法的效果。

为了更准确地分析对比各方法的性能，需要将二元组做停词筛选： 如二元组包含停词表中的字，则将其剔除，不做考虑。本文所使用的停词表包括文言助词、虚词以及数词的简约停词表，共26字： “之乎者也是于於何而以為所不無其曰一二三四五六七八九十”。

从语料库中抽取二元组后，可以根据第二节中介绍的统计模型，计算组成二元组的两个字的关联强度值，按其排序，取出排名靠前，或关联强度值大于某一阈值的若干二元组，得到最终结果集。本文使用的《史记》全文语料，排除表格等无语句信息的部分，并经过停词处理后，共保留501 995字，其中产生的二元组的次数(token)为283 052，形数(type)为110 409。

从熟语料中统计出所有双字词及其实际频率(Actual Frequency，即双字词在熟语料中出现的频率)，数据如表3所示。

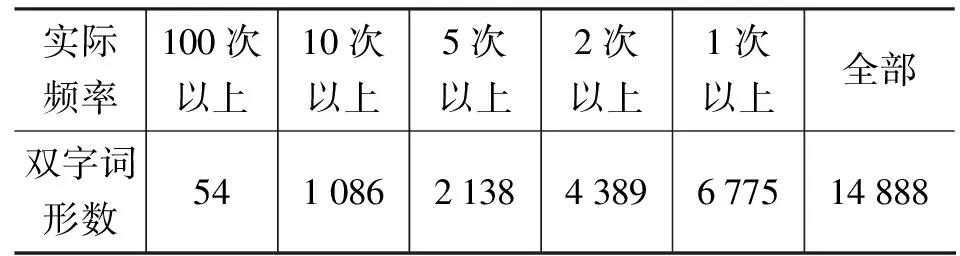
表3 熟语料库中双字词统计频度

实际频率大于100的双字词及其实际频率如表4所示。

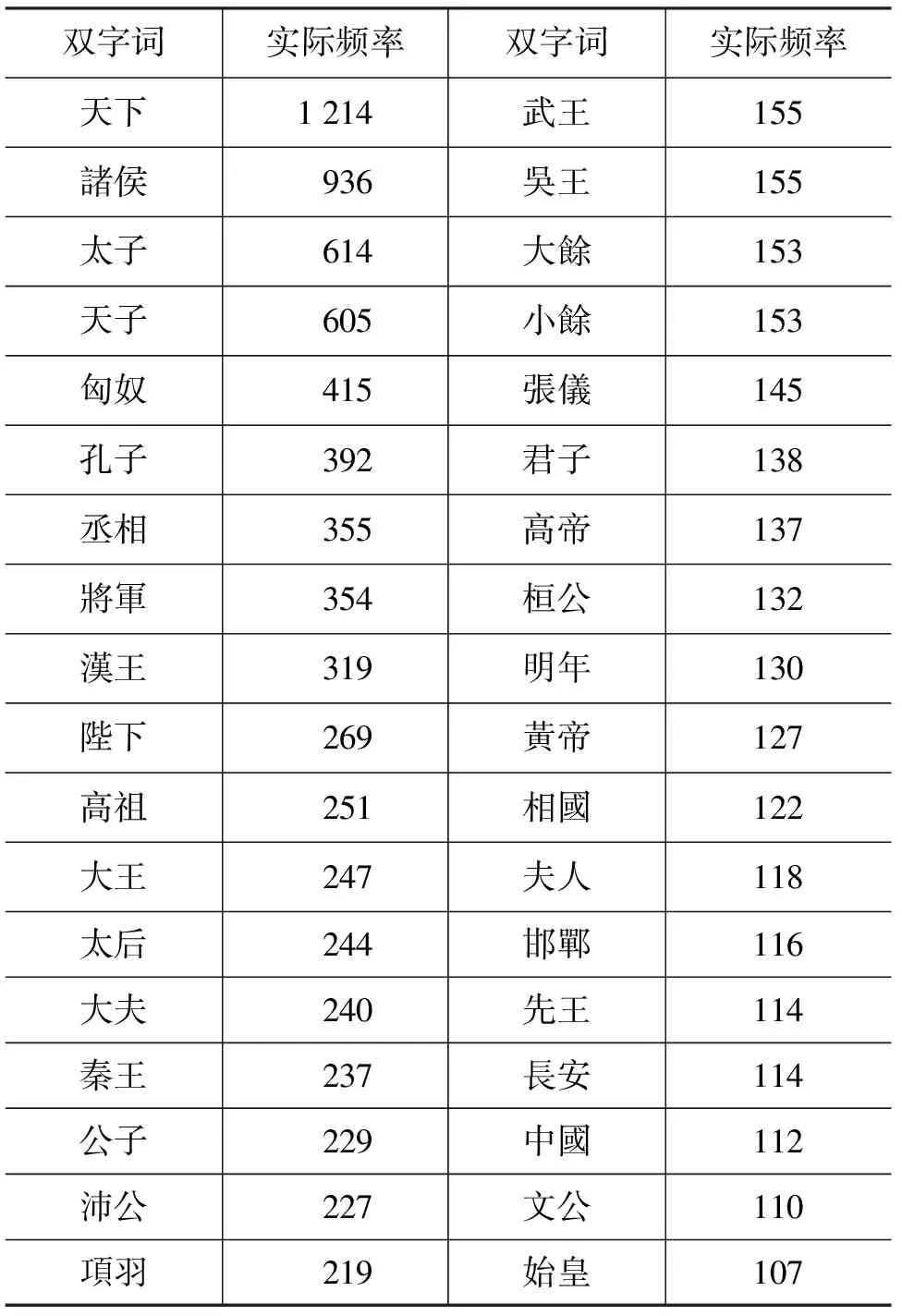
表4 实际频率为100以上的双字词

续表

为观察各方法的性能，表5列出了经各方法计算后，将统计指标最高的前N项结果作为结果集时，该结果集的准确率。图1列出了随着保留数的变化，各方法准确率的变化趋势。

从表5和图1中可以看出，总体上三次互信息的准确率明显高于其他方法，其次是似然比；频率、点互信息、t检验、卡方检验在结果集的保留数不同时，曲线走向又有各自的特点。随着保留数的增加，所有方法的准确率都呈现出缓慢下降，并逐渐趋于平稳的趋势。下面结合每种方法获取到的前20项结果，对各自的获取性能和特点进行说明。

表5 各方法结果集在保留数取不同值时的准确率

图1 各方法结果集在保留数的不同取值下的准确率的散点图

3.1 频率

从表5和图1可以看出，基于频率的获取方法在获取高频双字词方面表现尚可，但随着保留数的增加，该方法的准确率下降得很明显。在保留数达到2 000时，准确率已经下降到了50%以下。可见在大量地获取双字词方面，基于频率的获取方法表现得并不理想。表6列出了观察频率(区别于实际频率)最高的前20个二元组及其相关信息(本文所使用的词类系统为中国台湾“中央研究院”发布的上古汉语词类标记系统，所列出的双字词的词类为该词在熟语料中出现次数最多的词类，下同)。

表6 观察频率最高的前20个二元组及其相关信息

续表

显而易见，同现频率很高的两个字在很多情况下并不是双字词，而很可能是一个功能性短语，例如，“以為”、“而不”、“之所”等。虽然经过停词处理后，过滤掉了很多功能性短语，但还是不可避免地出现不是双字词的短语，如表6中的“使人”。该方法的优点为计算简单，运行速度快，缺点是会抽取出很多包含常用字的非词二元组，而且因为其完全依赖于频率，这就使得其无法获取到低频率双字词，所获取的双字词的词类也以常出现的集体名词和有生名词等常见的词类为主。如果对结果精度要求不高，不需要获取特定词类的双字词，并且只希望迅速找出高频率的双字词，利用一个设计合理的停词表，基于频率的获取方法不失为一个较好的选择。

3.2 点互信息

从表5和图1可以看出，在保留数较小的区域，点互信息的走势会出现一个小幅波峰，而且这种方法对于低频二元组的获取性能明显低于其他方法，这也印证了本文在2.3.1节的论述。然而利用点互信息对低频事件赋予较高值的特点，我们可以通过过滤掉低频二元组，从而获取到特定频率范围内的双字词。表6列出了过滤掉观察频率小于等于10的二元组后，点互信息最高的前20个二元组及其相关信息。

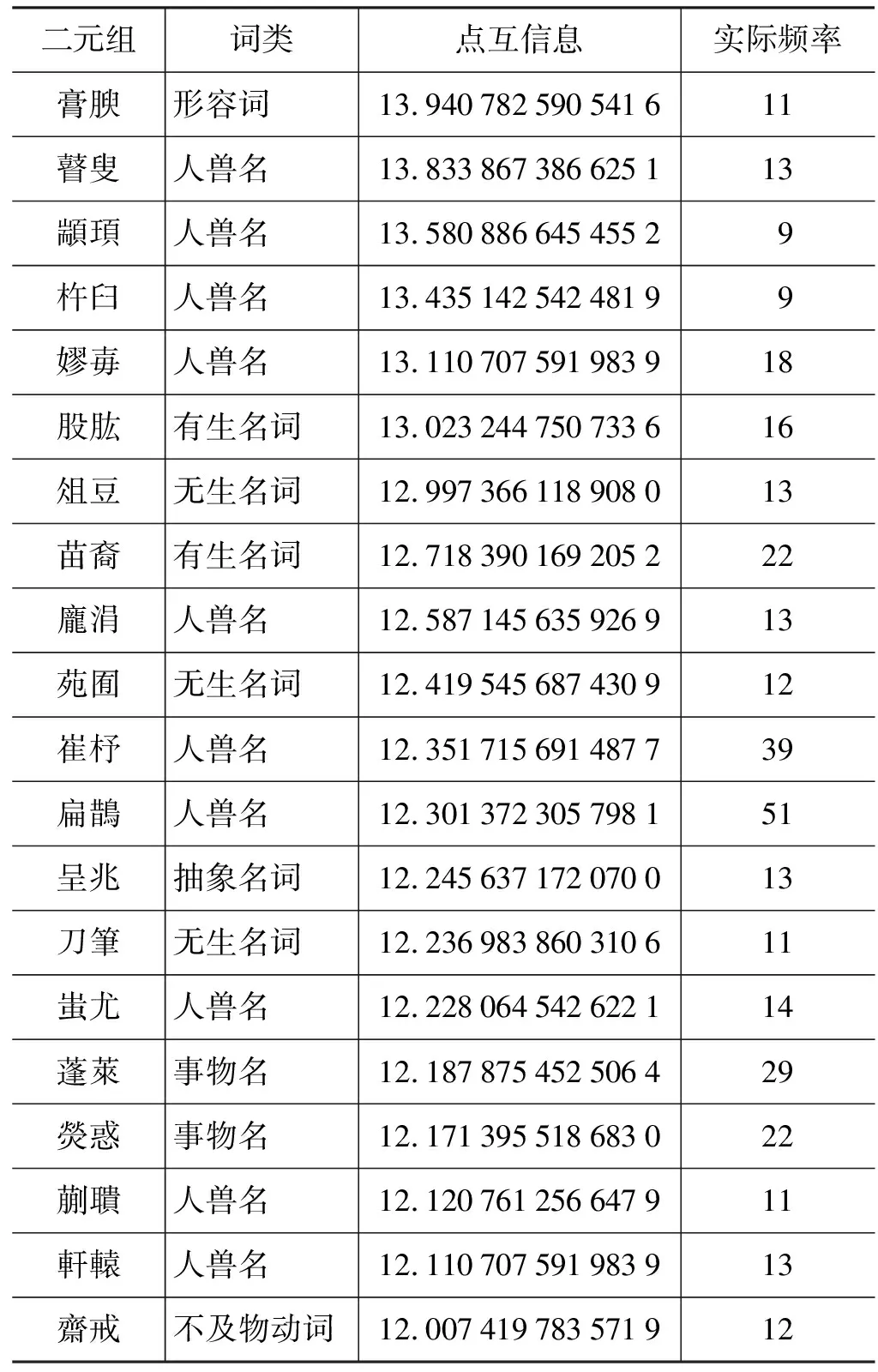
表6 点互信息值最高的前20个二元组及其相关信息(观察频率大于10)

经计算，观察频率大于10，并且点互信息最高的前100个二元组组成的结果集，其准确率达到了90%。从表6可以看出，其获取的结果在熟语料中作为双字词时出现的次数基本处于10到20之间，所获取的双字词的词类不再局限于常出现的集体名词和有生名词，而是更加偏重于特定频率下的人兽名和事物名等命名实体。由此可见，在获取特定频率范围内的双字词方面，点互信息有很好的性能。同时，对点互信息值最小的100个二元组进行统计，其中只包含11个双字词。可见，点互信息也可以应用于检验二元组中两个字的无关性。

3.3 三次互信息

从表5和图1可以看出，三次互信息在点互信息的基础上，很好地解决了数据稀疏问题。它的结果集在保留数取不同的值时，准确率均明显高于其他方法，是一种简单高效的方法。表7列出了三次互信息值最高的前20个二元组及其相关信息。

表7 三次互信息值最高的前20个二元组及其相关信息

从表7可以看出，虽然三次互信息方法的准确率较高，但其所获取的双字词的词类特点不鲜明。既有人兽名、事物名等命名实体，又有集体名词、有生名词等非命名实体，并且无法获取到特定频率下的双字词。如果对获取结果没有特殊的需求，三次互信息是六种方法中的最佳选择。

3.4 t检验

从表5和图1可以看出，随着保留数的增大，t检验准确率的走势基本与三次互信息和似然比相同，但准确率均低于两者，可见在大量获取双字词方面，它并不是一个很好的选择。但t检验对低频事件的处理较好。所以对于稀疏数据，它比互信息和卡方检验更有优势。表8列出了t检验值最高的前20个二元组及其相关信息。

遗憾的是，表8并没有反映出t检验的结果集有何种特点。t检验的一个问题在于它的前提假设，它认为数据满足正态分布[2]。而将其应用于《史记》双字词获取时效果并不突出，这也反映出在自然语言中(至少在《史记》中)，词汇的出现概率往往不满足正态分布。

表8 T检验值最高的前20个二元组及其相关信息

3.5 卡方检验

从表5和图1中可以看出，随着保留数的增加，卡方检验的准确率趋势大体与似然比相同，但与点互信息类似，在保留数100到500之间，卡方检验的准确率会出现一个波峰，并且卡方检验的波峰与互信息的相比更加明显。由此可见，卡方检验比点互信息更加倾向于为低频二元组赋予较高的值，这也反映出卡方检验的不足在于当保留数量很小时，结果的说服力不是很强[2]，因此获取得到检验值较高的二元组中会出现更多的低频词。表9列出了t卡方检验值最高且观察频率大于10的前20个二元组及其相关信息。

表9 卡方检验值最高的前20个二元组及其相关信息(观察频率大于10)

经计算，观察频率大于10，并且卡方检验最高的前100项组成的结果集，其准确率达到了92%，高于点互信息的90%。通过对表9列出的结果进行分析，可以看出，根据卡方检验抽取的二元组中命名实体所占比例较大。另外，在卡方检验值最小的100个二元组中只有4个是双字词(常民/有生名词、陳定/人兽名、上德/抽象名词、餘閒/抽象名词)，所以无论是获取特定频率双字词，还是检验二元组中两个字的无关性，卡方检验的性能均好于互信息，是六种方法中的最佳选择。

3.6 似然比

从表5和图1可以看出，在保留数取不同的值时，似然比的结果集表现较好，仅次于三次互信息。表10列出了似然比对数值最高的前20个二元组及其相关信息。

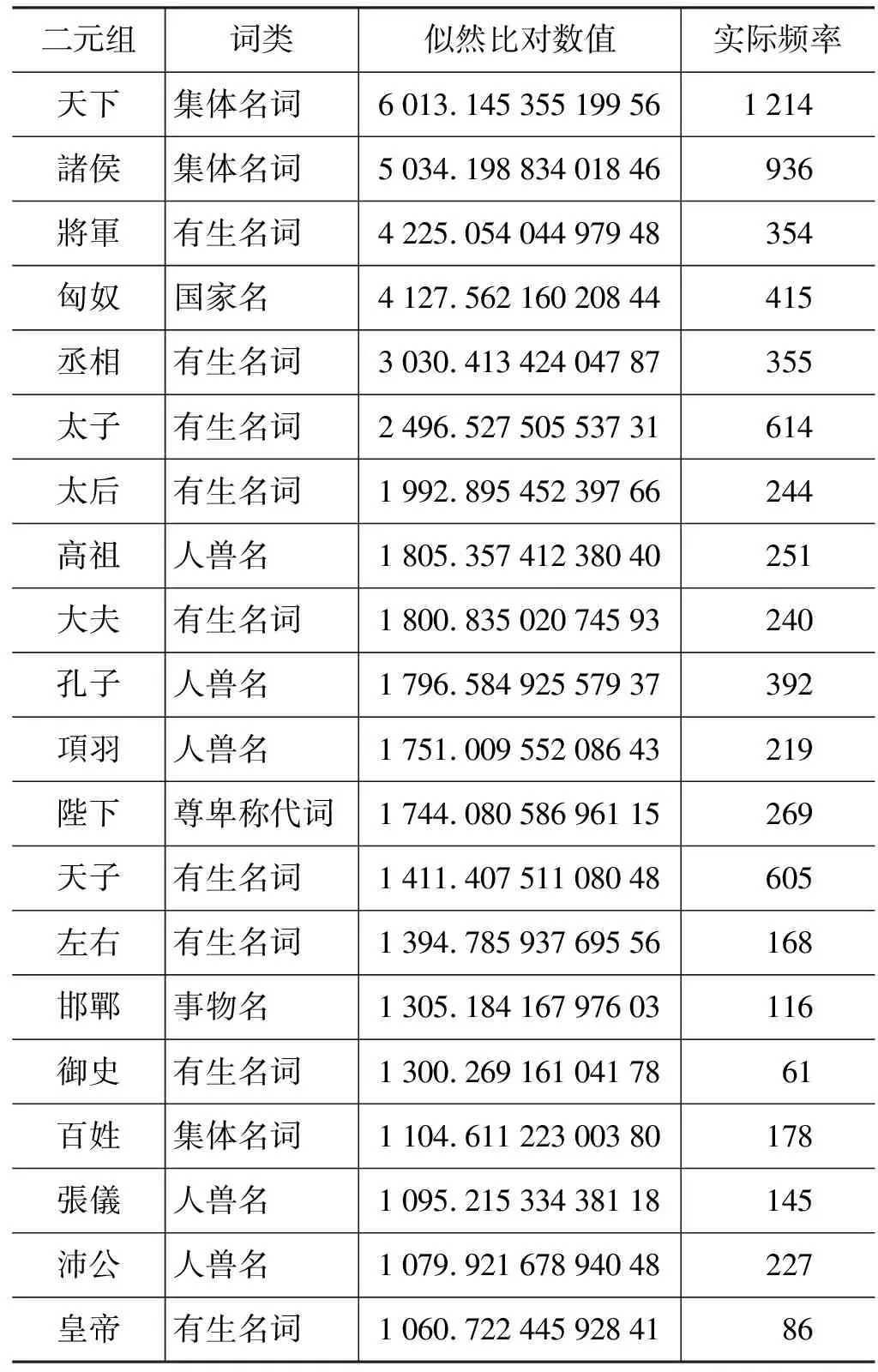
表10 似然比值最高的前20个二元组及其相关信息

从表10可以看出，与三次互信息类似，似然比所获取的双字词的词类特点也不鲜明。鉴于其在整体获取性能方面的表现，似然比是假设检验中最适合获取双字词的方法。

4 结论

本文介绍了六种针对古汉语双字词自动获取的方法，从《史记》全文语料库中自动获取二元组，在对获取结果进行分析的基础上对比了各方法的不同特性，提供了根据应用需求的不同，进行古汉语双字词自动获取的相应解决方案，如表11所示。

表11 各统计模型在双字词获取上的适用需求

如对获取结果准确率要求不高，但对运行时间和方法简易度有一定要求，可以使用基于频率的获取方法；如对获取结果准确率要求较高，但对获取的词类偏重无要求，可以选择基于三次互信息的获取方法；如欲获取特定频率范围内的双字词，可以首先设定频率阈值进行过滤，然后使用基于卡方检验的方法进行获取。

上述方法可以应用于诸如命名实体识别、分词、机器翻译、文本分类、句法分析、词典编纂等需要识别词语结构和内容的自然语言处理领域。

目前，还无法对多字词进行自动获取。因此，今后将在这个方面进行进一步的研究。

[1] 王宁.古代汉语[M].北京： 北京出版社，2002.3-4.

[2] 苑春法，等译.统计自然语言处理基础[M].北京： 电子工业出版社.2007: 94-117.

[3] 全昌勤，刘辉，何婷婷.基于统计模型的词语搭配自动获取方法的分析与比较[J].四川成都： 计算机应用研究.2005，(9)：61-63.

[4] Christopher D. Manning Hinrich. Foundations of Statistical Natural Language Processing[M]. The MIT Press Cambridge, Massachusetts London, England，94-117.

[5] 陈章太.点互信息世纪之交的中国应用语言学硏究[M].北京： 华语教学出版社，1999.495.

[6] Oakes M. Statics for Corpus Linguistics [D].Edinburgh： Edinburgh University Press，1998: 171-172.

[7] 盛骤，谢式千，潘承毅.概率论与数理统计[M].北京： 高等教育出版社.2005: 162-170.

[8] 李时.应用统计学[M].北京： 清华大学出版社，2005: 68-73.