无轴承异步电机的感应补偿控制研究

卜文绍，袁澜，肖隽亚，刘文胜

（河南科技大学 电子信息工程学院，河南 洛阳 471003）

1 引言

无轴承电机的电磁转矩和磁悬浮力产生之间存在着基于转矩系统气隙磁场的耦合关系。悬浮控制系统磁场会在转子绕组中产生感应电动势和电流，从而会导致有效悬浮控制（激磁）电流在幅值和相位上的变化，影响悬浮控制性能。因此，如何对悬浮系统进行有效的感应补偿，也是实现无轴承电机稳定高精度悬浮控制的关键问题。

关于无轴承电机控制，国内外已有不少研究成果［1－9］。本文将对无轴承异步磁悬浮控制系统的转子感应问题及其补偿控制方法进行研究分析，同时给出4极转矩系统转子磁场定向控制模型和气隙磁场的幅值、相位信息的在线计算方法。

2 悬浮系统的感应补偿控制策略

无轴承电机的悬浮力是由转矩系统和悬浮系统之间的气隙磁场相互作用而产生的。悬浮控制系统一般采用气隙磁场定向控制策略，但旋转的悬浮控制磁场将在转子绕组中感应出电流。在悬浮系统采用电流跟踪控制逆变器时，悬浮系统转子感应电流将导致悬浮控制电流命令和实际产生的悬浮绕组控制（激磁）电流在幅值和相位上的差异，从而导致磁悬浮力命令和实际磁悬浮力间出现幅值和相位上的偏差。

在电机稳定悬浮运行中，转子径向偏心位移一般远小于电机平均气隙。忽略由于转子微弱偏心引起的两套绕组间的耦合互感影响，悬浮控制绕组的单相等效电路如图1所示。

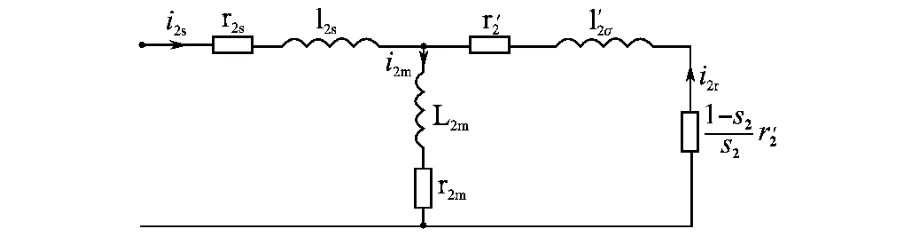
图1 悬浮控制绕组等效电路Fig.1 Equivalent circuit of suspension windings

由图1可知，悬浮绕组电流与其中激磁电流间的传递函数为

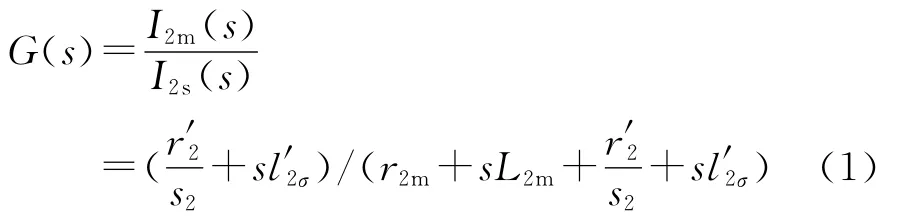
对于2极悬浮控制4极无轴承异步电机，电机转速决定于4极电机磁场的转速。相对于2极悬浮磁场，转子转差率约0.5，即s2≈0.5。

图2是根据样机参数为：r2m＝3.5Ω，L2m＝0.230H，r′2＝2.344Ω，绘制的G（jω）对数频率特性伯德图。

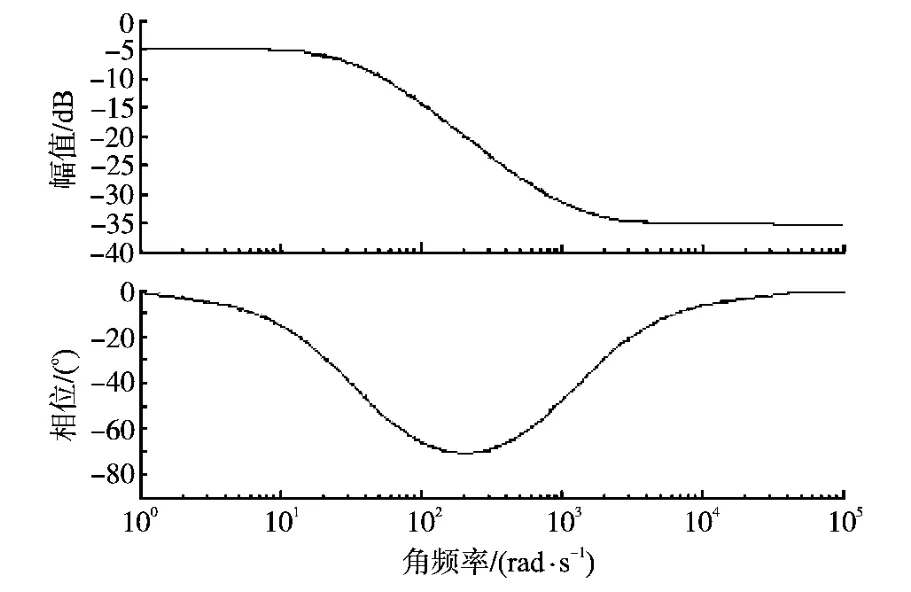
图2 2极悬浮控制绕组L2m／l2s的对数频率特性Fig.2 L2m／l2sBode map of two－pole suspension windings

从图2可看出：相比定子悬浮绕组电流，控制（激磁）电流在幅值上减小，相位上滞后。

1）在低频段，可以不考虑转子漏感的影响，悬浮绕组电流和其中的控制电流分量之间的关系可基本用典型惯性环节近似。

2）随着角频率的升高，定子电流和励磁电流之间的幅值和相位偏差逐渐增大；在角频率达到200rad／s时，相位偏差达到最大值约70°，幅值偏差近20dB。

3）随着工作频率的进一步增加，相位偏差逐渐回落，而幅值偏差继续增大；到工作频率约2000rad／s时，幅值偏差基本稳定在35dB，到工作频率达到30000rad／s时，相位偏差基本消除。

4）高频段频率特性基本决定于转子绕组漏感和悬浮绕组的激磁电感参数。

悬浮控制电流与悬浮绕组电枢电流之间的关系可表示为

式中：Krc为定子悬浮绕组电流矢量和其中的激磁电流矢量幅值之比；θrc为实际控制（激磁）电流滞后于实际绕组电流的电角度。

如把悬浮绕组电流i2sm和i2st当作悬浮控制电流，相应的悬浮控制力命令信号为

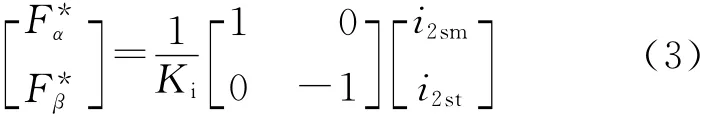
根据式（2）和式（3），可得到实际产生的转子磁悬浮力和悬浮力命令信号之间的关系为

从式（2）、式（4）可看出，如果不考虑转子感应电流的影响：

1）当实际悬浮控制电流分量在幅值上比悬浮绕组电流小Krc倍时，实际产生的磁悬浮力也比悬浮力命令小Krc倍；

2）悬浮控制电流分量在相位上比悬浮绕组电流滞后θrc（电角度）时，实际产生的磁悬浮力将在相位上比悬浮控制力命令超前θrc（机械角度）。

实际产生的磁悬浮力和其命令信号在幅值和相位上的不一致，将导致悬浮控制精度的降低和沿两静止坐标轴向上磁悬浮控制力分量之间的耦合。为克服悬浮磁场感应转子电流的影响，本文采用超前幅相补偿法进行校正，以改善控制性能。

取校正环节：

其中

在悬浮控制电流命令后串联超前幅相补偿环节后，得悬浮绕组电流命令信号：

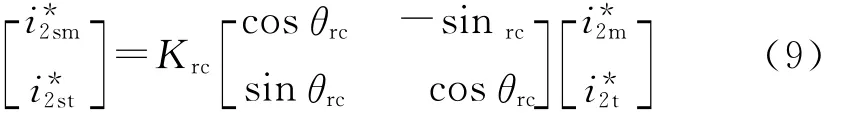
3 控制系统仿真分析与实验

图3为所设计的三相无轴承异步电机磁悬浮控制系统结构。因转子磁场定向控制有优良转矩控制性能，转矩驱动系统采用了转子磁场定向方式；悬浮控制系统采用气隙磁场定向控制，并按式（9）进行幅相感应补偿。为实现准确、可靠的磁悬浮解耦，需获取转矩系统的气隙磁链信息。

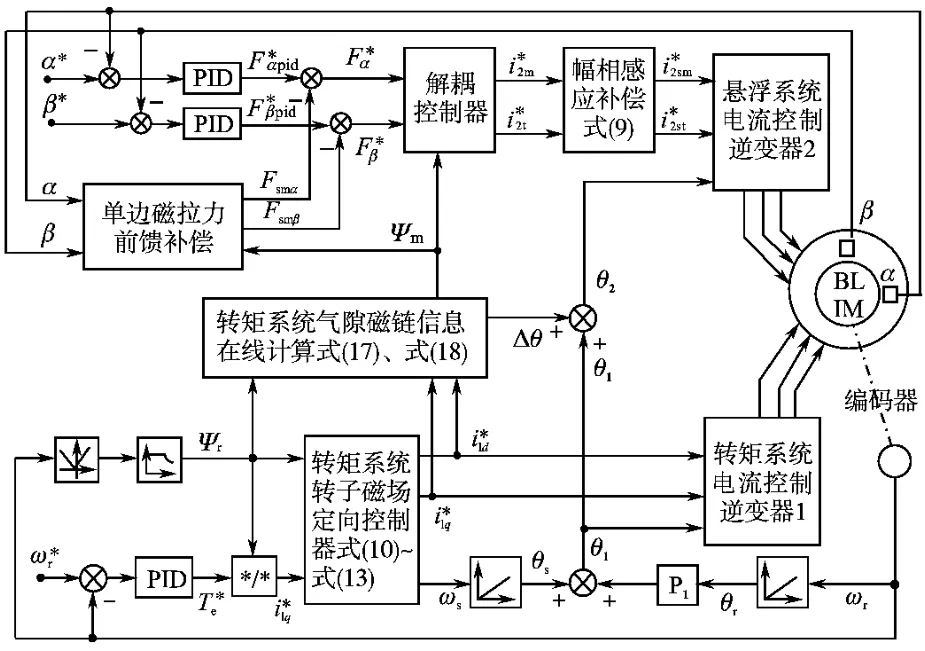
图3 三相无轴承异步电机解耦控制系统结构图Fig.3 Decouple control system of three－phase bearingless induction motor

3.1 转矩系统气隙磁链信息的实时计算

根据电机控制原理，结合转子磁场定向控制约束条件“Ψrd＝Ψr，Ψrq＝0”，得转矩系统的电流、转差角频率及电磁转矩表达式［2］：

转子磁场定向方式下，4极转矩系统的气隙磁链可表示为

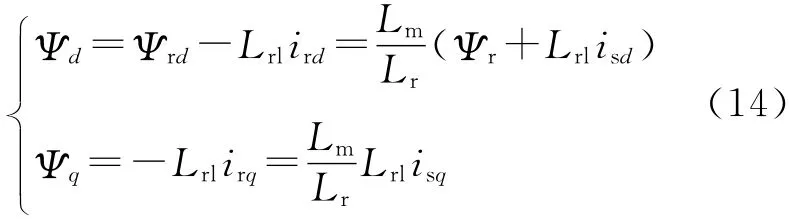
根据式（14），可以得到气隙磁场偏离转子定向磁场的电角度和气隙磁链幅值：

在电流不是很大的情况下，漏感磁链相对于转子磁链Ψr很小，有以下近似公式：

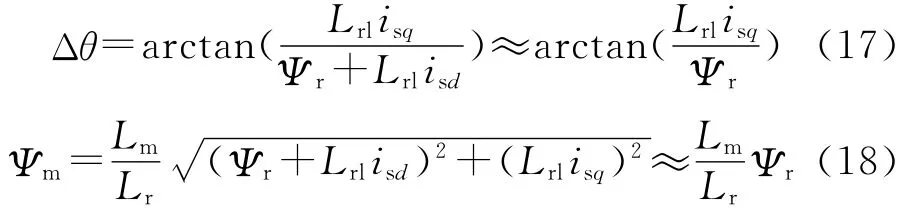
3.2 系统仿真分析与实验

参数设置为：1）4极转矩系统，2.2kW，R1s＝1.6Ω，L1l＝0.0043H，R1r＝1.423Ω，L1rl＝0.0043H，Lm1＝0.0859H，J＝0.024kg·m2；2）2极悬浮控制系统，R2s＝2.7Ω，L1l＝0.00398 H，R1r＝2.344Ω，L1rl＝0.00398H，Lm2＝ 0 .230 H；3）应急辅助轴承单边平均气隙200μm；4）转子重10kg，质量偏心率0.1%。

图4是不带径向负载时的磁悬浮解耦控制系统的转子径向位移变化波形。图3a为转子轴心沿α轴向的径向位移变化波形；图3b为转子轴心沿β轴向的径向位移变化波形。

图4 空载启动时径向位移变化波形Fig.4 Radial displacements waves with none load startup

从图4可以看出，采用该控制系统，在加速启动和转速稳定后的整个过程中，转子轴心始终在大约±40μm径向位移范围内变化，系统始终处于稳定悬浮运转状态。

图5给出了0.7s时刻突加径向负载时的情况。图5c为径向力负载变化情况；图5d和图5e给出了添加突变径向负载前后，磁悬浮控制力命令信号的变化波形。

由图5可看出：1）在添加突变负载之前，沿α和β两坐标轴向的悬浮力命令基本都在零值附近上下波动，不产生平均径向静态磁悬浮力；2）在添加β坐标轴向突变负载瞬间，沿β坐标轴向径向位移出现轻度偏心，在控制系统作用下，沿β坐标轴向磁悬浮力命令发生相应突变，以产生β轴向静态磁悬浮力来平衡突变的外部径向负载，使转子迅速恢复到定子中心位置处；3）而从稳定运行到沿β轴向突变径向负载力的整个过程中，沿α坐标轴向的磁悬浮力命令信号没有发生任何关联性变化，仍然在零值附近做上下波动，α轴向的径向位移也未产生关联性变化，表明沿两坐标轴向实现了良好的解耦控制。

图5 沿β向突加300N径向力负载前后的波形Fig.5 Operation waves when adding 300Nradial load

图4、图5中的径向位移量和图5中的悬浮控制力命令等都呈现出了周期性波动特征，原因是在系统仿真模型中，人为加入了不可避免的转子质量偏心的影响（此处预设质量偏心率为0.1%）。

图6 磁悬浮解耦控制装置径向位移实验波形Fig.6 Experimental waves of magnetic suspension decouple control equipment

根据本文磁场定向和补偿控制策略，采用单TMS 320LF2407A控制方案，设计了三相无轴承异步电机磁悬浮解耦控制系统实验装置，基于三相无轴承异步电机样机，进行了稳态悬浮运行控制实验，实现了稳态悬浮控制。图6为沿α和β两坐标轴向的稳态悬浮运行位移波形。

4 结论

本文首先分析了悬浮控制系统转子绕组感应现象导致的磁悬浮力相位、幅值偏差问题。然后详细分析了转子绕组的感应补偿校正措施；最后，根据无轴承异步电机的运行控制特点，给出了三相无轴承异步电机悬浮运行控制系统结构，转矩系统采用转子磁场定向、悬浮系统采用气隙磁场定向及幅相感应补偿相结合的组合控制策略，并介绍了4极转矩系统转子磁场定向控制方式下，气隙磁链幅值、相位信息的在线计算方法，对磁悬浮解耦控制系统进行了仿真分析和实验。仿真和实验结果表明了本文所给出的磁悬浮系统转子感应补偿控制策略的可行性和有效性。

［1］邓智泉，王晓琳.无轴承异步电机的转子磁场定向控制［J］.中国电机工程学报，2003，23（3）：89－92.

［2］王晓琳，邓智泉.无轴承异步电机磁场定向控制策略分析［J］.中国电机工程学报，2007，27（27）：77－82.

［3］柏仓，黄守道.无轴承永磁同步电机无位移传感器系统建模与仿真［J］.电气传动，2009，39（9）：60－63.

［4］张汉年，张涛.无轴承同步磁阻电机解耦集成控制策略［J］.电气传动，2009，39（9）：56－59，79.

［5］魏劲夫，朱熀秋，于晶.无轴承永磁同步电机启动控制研究［J］.电气传动，2011，41（2）：61－64.

［6］管晓文，黄守道，高剑.永磁型无轴承电机悬浮力前馈控制系统研究［J］.电气传动，2009，39（3）：40－43.

［7］Chiba A，Akamatsu D.An Improved Rotor Resistance Identific ation Method for Magnetic Field Regulation in Bearingless Induction Motor Drives［J］.IEEE Trans.on IE，2008，55（2）：852－860.

［8］Miyamoto N，Enomoto T，Amada M，et al.Suspension Characteristics Measurement of a Bearingless Motor［J］.IEEE Trans.on Magnetics，2009，45（6）：2795－2798.

［9］Bu Wenshao，Huang Shenghua，Wan Shanming.General Analytical Models of Inductance Matrices of Four－pole Bearingless Motors With Two－pole Controlling Windings［J］.IEEE Trans.on Magnetics，2009，45（9）：3316－3321.