级联式逆变器故障单元旁路下输出平衡的椭圆校正法
张德宽,张军军,乔奕玮,尹雷
(天津方圆电气有限公司,天津 300350)
1 引言
高压级联式逆变器单元故障后多采用单元输出旁路方法剔除相应的故障单元,并使剩余单元组成降级拓扑结构,维持系统继续工作。简单的旁路方法为等位旁路法,即某相某单元故障后,将另外两相相同级位上的正常单元同时旁路,以达到输出平衡的目的。自国外学者提出中性点漂移方法后[1],极大地引起人们的兴趣。目前,非平衡拓扑结构下的中性点漂移方法几乎成了级联式高压变频故障单元旁路后实现输出平衡的不二选择。中性点漂移方法的巨大优势在于仅旁路(剔除)故障单元,在非平衡拓扑结构下实现逆变器输出(基波)平衡,并尽可能高的保证其输出电压利用率。目前,国内学者所演绎的方法大多为离线角度计算法,即将逆变器全部故障旁路拓扑状态下所对应的偏移角度一一算好存入表格,以备逆变控制器实时查取[2-3]。而面向不同电压等级所采用不同的拓扑结构,这种方法离线计算工作量显得相当繁重,灵活性较差,不利于产品系列化。且在以磁场定向原理实现的控制策略当中,电压指令通常以d-q轴的实时分量给出,若实现角度偏移必须将目标参考电压指令转化为极坐标形式,然后再由极坐标形式变换为三相时域正弦指令方能添加偏移角度,这其中还要涉及到反正切函数的查表运算,从而影响软件实施效率。
本文基于逆变器输出电压矢量圆形轨迹为原则,提出一种椭圆轨迹电压指令补偿逆变器拓扑结构所产生的不平衡的控制策略,实现了逆变器输出线电压输出平衡。该方法不需要计算偏移角度,只需已知逆变器故障旁路单元数(或剩余单元数),并对参考电压指令进行椭圆轨迹校正即可,简化了控制算法。结合非等量谐波注入,该方法可以实现最高输出电压利用率。
2 故障旁路状态下输出平衡的椭圆轨迹校正方法
2.1 逆变器电压矢量与负载相电压矢量的关系
级联式逆变器主电路如图1所示。

图1 级联式逆变器主电路Fig.1 Power stage of cascaded inverter
设x为空间任意电压参考点(如高压逆变器公共点“N”),“0”为等效电机中性点。则逆变器侧输出相电压可分别表示为Uax,Ubx,Ucx;电机侧输出电压表示Ua0,Ub0,Uc0,则逆变器公共点对电机中点电压为Ux0,存在下列关系:

代入电压矢量定义式得电机侧电压矢量为

可见:逆变器相电压矢量与等效星型电机负载电压矢量完全相同,若保证输出平衡只需要保证逆变器在任何条件下输出电压矢量基波轨迹为理想圆即可。
2.2 故障旁路状态下逆变器输出电压轨迹特征
设级联式逆变器原始单元数为N,故障旁路后三相所剩单元数为Na,Nb,Nc。则三相电压剩余单元系数分别为 Na/N,Nb/N,Nc/N。在原始参考电压指令不作任何修正的情况下,由于故障旁路不平衡所形成的逆变器输出电压矢量表达式为

式中:Ve为原始额定相电压。
将式(5)化简为直角坐标系的实部和虚部,不难得出其解析函数为椭圆轨迹。只是不同系数的组合椭圆轨迹的长轴、短轴及与实轴夹角有所不同。图2给出了9单元逆变器剩余单元数[Na,Nb,Nc]=[5,7,9]时,电压合成矢量的仿真轨迹。由图2可见输出电压矢量轨迹表现为非理想圆形(椭圆),因此必然会带来输出电压的不平衡(此处仅给出典型单元故障状态的电压矢量轨迹,其他故障状态情况雷同)。
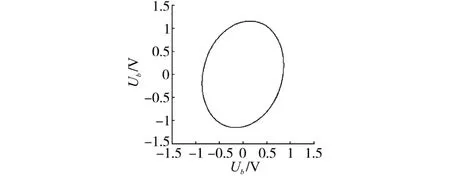
图2 旁路状态[5,7,9]无校正输出电压轨迹Fig.2 Simulation trajectory of output voltage without correction in bypass state[5,7,9]
2.3 椭圆轨迹校正原则
既然原始(圆形)参考指令电压矢量轨迹施加到故障旁路结构的逆变器拓扑后,输出电压轨迹表现为椭圆,那么,是否存在1个特定的椭圆指令轨迹而使故障旁路状态下的输出电压轨迹为理想圆形呢?解析几何方法不难证明,只要选择1个与图2所示椭圆长轴垂直的椭圆作为目标参考矢量轨迹,则逆变器最终的输出电压矢量轨迹将被校正为理想圆形轨迹,如图3所示。此即本文提出的椭圆轨迹校正原则。
图3虚线框内给出了本文所提方案的具体实施策略,其中包括椭圆轨迹校正和非等量谐波注入两部分。图3中Uα,Uβ为原始参考指令,稳态表现为理想的圆形轨迹。e-jπ/2为预旋转,此为保证整个变换过程参考指令相位角一致(若控制模式仅考虑VF控制模式,不强调严格的相位关系可忽略前级的预旋转变换)。由于参考指令轨迹为圆形,经e-jπ/2逆时针预旋转后其轨迹形状不会改变,即Uα1,Uβ1轨迹仍为圆形。2-3变换后得到三相电压指令Ua,Ub,Uc,再经幅值变换后得到逆变器旁路状态下的观测模型,即Ua1,Ub1,Uc1相当于理想指令下对应的逆变器输出,不难理解,U′α-U′β所表现的轨迹为椭圆,如图2所示。经ejπ/2垂直变换(顺时针旋转π/2),即得到我们所希望的参考矢量指令。以下为该模型的具体算法。

图3 椭圆轨迹校正和非等量谐波注入控制模型Fig.3 The control model of elliptical trajectory correction with non-equivalent harmonic injection
2.3.1 e-jπ/2预旋转变换

2.3.2 2-3变换
由电压矢量原始定义式得

2.3.3 幅值变换
Na为级联逆变器a相剩余单元数;Nb为级联逆变器b相剩余单元数;Nc为级联逆变器c相剩余单元数;N为级联式逆变器原始单元数。该变换环节与谐波注入法对接即可达到平衡逆变器输出的目的。
2.3.4 ejπ/2旋转变换(垂直变换)

2.3.5 幅值补偿 K
由于幅值变换和垂直变换会导致参考信号幅值降低。为此,通过幅值补偿来提高参考信号幅值,从而保证逆变器输出电压利用率。
2.4 非等量谐波注入
因椭圆轨迹校正基于参考信号理想正弦条件,逆变器输出电压并未得到最大程度的利用。为此,椭圆轨迹校正后参考信号需注入3次谐波,以形成幅值减低的马鞍形参考信号,提高输出电压利用率。国外学者在文献[1]中提出等量3次谐波注入法,由于旁路状态下主电路拓扑结构失去原有的对称关系,势必表现出输出谐波的不对称性,以致逆变器输出电流矢量轨迹发生畸变。为此,本文提出非等量3次谐波注入法,该方法不仅能够提高输出电压利用率,而且保证了输出电流轨迹为理想圆形。图4给出了非等量3次谐波注入法的原理框图,图4中假设级联逆变器单元故障旁路状态下三相剩余单元数满足Na≤Nb≤Nc。其中Vmax和Vmin取的正包络线和负包络线。

图4 非等量谐波注入法原理框图Fig.4 Block diagram of the non-equivalent harmonic injection
3 仿真研究
为验证本文方法的理论可行性,依据实验室模拟样机的参数,在Matlab环境下构建系统模型,负载按等效Y型对称R-L负载考虑,其中R=5.6Ω,L=440mH。作为特例,本文仿真结果均在[Na,Nb,Nc]=[5,7,9]条件下进行。
结合前文图3中所给出的变量,图5给出了本方案所涉及典型轨迹的仿真结果。其中曲线A为原始参考指令Uα,Uβ的轨迹,曲线B 为U′α,U′β轨迹相当于原始指令条件下逆变器的观测轨迹,对应图2所示的轨迹。曲线C为重构的目标参考指令的轨迹。可见,曲线B和曲线C所表现的椭圆轨迹彼此垂直,不难理解,两者叠加的结果势必在逆变器输出侧表现为理想的圆形轨迹,从而获得三相平衡的输出电压(基波)。

图5 旁路状态[5,7,9]各参考指令仿真轨迹Fig.5 Simulation trajectory of reference signals in bypass state[5,7,9]
图6给出了采用本文方案逆变器输出接Y型R-L负载时的输出电流矢量的仿真轨迹。可见经椭圆校正后逆变器得到对称的三相输出电流,进一步验证前文的推论。
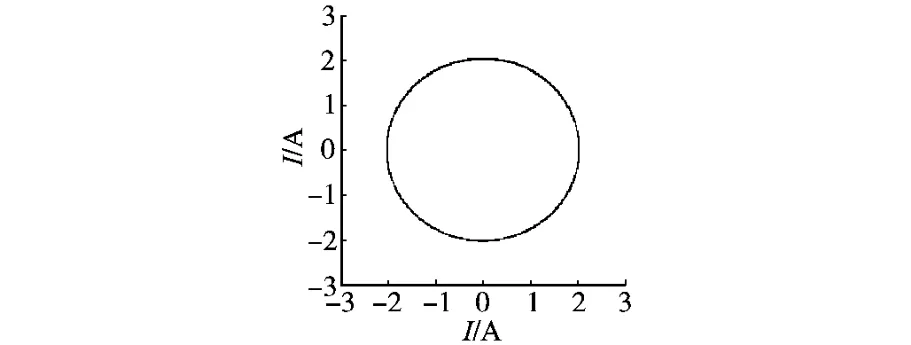
图6 旁路状态[5,7,9]输出电流仿真轨迹Fig.6 Simulation trajectory of output current in bypass state[5,7,9]
图7给出了旁路状态[5,7,9]下,逆变器带R-L负载时的输出电流、相电压和线电压仿真波形。可见因旁路所造成的逆变器相电压是不对称的,而输出线电压和负载电流却表现为所希望的对称关系。

图7 旁路状态[5,7,9]输出电流、电压仿真波形Fig.7 Simulation waveforms of output current and voltage in bypass state[5,7,9]
4 实验
为进一步验证本文方案的正确性,特按未来10kV工业产品的拓扑结构在实验室搭建了1台级联式逆变器模拟机。模拟机主要参数为:原始单元数N=9,单元直流电压Vdc=42V;额定输出电压Ue=380V;额定电流Ie=3A。试验电机参数为:额定功率1.1kW,额定电压380V,额定电流2.8A。为便于与仿真结果比对,以下实验波形均在旁路状态[Na,Nb,Nc]=[5,7,9]条件下取得。
图8和图9分别给出了旁路状态[5,7,9]条件下椭圆校正逆变器输出相电压和线电压波形,其中VU表示U相电压,VUV表示U与V之间线电压,依此类推。图10给出了以上条件下的U,V两相输出电流实测波形,其中纵轴标度1A/100mV。

图8 旁路状态[5,7,9]校正后输出相电压波形Fig.8 Waveforms of the output phase voltage after elliptical correction in bypass state[5,7,9]

图9 旁路状态[5,7,9]校正后输出线电压波形Fig.9 Waveforms of the output line voltage after elliptical correction in bypass state[5,7,9]
由图8~图10可知,实验波形与仿真波形具有很大程度上的相似。基于椭圆轨迹较正原理和非等量谐波注入方式的级联式逆变器,旁路故障单元后,表现为输出的相电压幅值不等,但线电压幅值对称,而线电压对称即可保证电机侧的电流平衡。

图10 旁路状态[5,7,9]校正后电流波形Fig.10 Waveforms of the output current after elliptical correction in bypass state[5,7,9]
为考核本文方案输出电压利用率,特将逆变器原始拓扑[Na,Nb,Nc]=[9,9,9]和旁路状态下[5,7,9]的理论计算值及实测值进行比对,如表1所示。表1中η为离线角度计算方法[2]算出的逆变器理论最大输出电压利用率。实验测量的线电压值略大于理论计算值是因为使用数字万用表所测电压含谐波成分所致。

表1 逆变器输出线电压平均值(VAC)*Tab.1 Mean of the output line voltage of the inverter
由表1中数据可看出基于椭圆轨迹校正原理的中性点漂移法,逆变器旁路后输出线电压能够达到剩余单元相应的理论计算值,即理论最大输出线电压值。
5 结论
椭圆轨迹校正原理基于逆变器电压矢量合成原则,只需获取故障剩余单元数即可构建控制模型,避开了复杂的离线偏移角度的计算,且控制策略简便,实时性好,适合任意故障单元旁路状态下的输出平衡控制。参考信号注入非等量3次谐波,不仅能保证逆变器输出电流合成矢量轨迹为理想圆形,且输出电压利用率也能够达到理论最大值。仿真和高压模拟机上的实验证明该方法切实可行,为后续10kV工业样机的工厂试验提供了有力的技术支持。
[1]Peter W Hammond.Enhancing the Reliability of Modular Medium-voltage Drives[J].IEEE Trans.Ind.Elec.,2000,49(5):948-954.
[2]臧义,孙红鸽,徐彬.级联逆变器单元故障处理方法研究[J].电气传动,2009,39(7):29-31.
[3]汪伟,蔡慧,陈卫民,等.单元串联式高压变频器功率单元故障处理技术的研究[J].电气传动,2010,40(12):12-16.

