一种简易的双曲拱坝放样方法

□郑之明（安徽安庆市水利局）

近年来，我国的中小型拱坝建设发展较快，因其体积小、造价低，且受力条件好，可就地取材等特点被广泛应用。但是，由于拱坝断面小，尤其是双曲拱坝，其形状多变，在工程施工中，为确保坝体的几何尺寸，须随时进行放样控制。笔者曾主持过多座拱坝工程施工，结合实际工作经验，总结出一套简易可行的拱坝放样方法，在此作一介绍，与同行商榷。

1.建立控制座标系

拱坝均坐落于狭窄的“V”或“U”河谷之中，坝区地形高低起伏大，放样控制不同于平地，无法用直尺进行测控，采用方向线交会法也不现实，为确保对坝体几何尺寸的控制，最简便的方法是通过角度控制来实现，因此必须在坝区布设平面和高程基本控制网，即控制座标系统，以控制整个工程的施工放样。

对于较大的工程，可采用技术先进的电子全站仪进行测控，而一般中、小型拱坝工程则可使用经纬仪进行测控，本文所介绍的方法适用于对中、小型拱坝工程施工的测控。

由于拱坝高度较大，应根据坝区左右岸地形分层设置测站（建议每层不少于4个），测站高程应高于被测点，确保对各控制（放样）点的通视。

一般书本中介绍的放样方法为前方交汇，而实际操作中因地形、地貌及坝肩开挖等因素，测站与坝肩难以通视，因此笔者推荐侧向交汇，即两测站同时设于拱坝的左或右岸，左两测站控制右端坝体，右两测站控制左端坝体，见测站平面示意图（图1）。

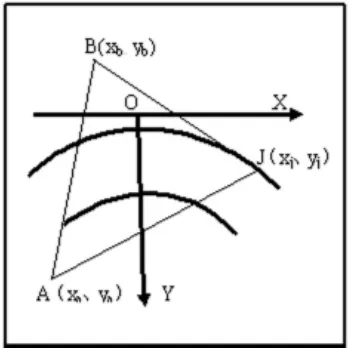
图1 测站平面示意图

2.计算原理

每座拱坝都有各自的设计座标系，坝体细部尺寸通过以设计座标原点O的立面轴线方程和平面轴线方程来反映，为便于计算，建议将坝体的设计座标转换至控制座标系。

每次放样一般为坝体的同一高程，放样的高程间隔应与施工的高程间隔相对应。当对某一高程坝面进行放样时，放样点的间距以1.0m左右为宜，首先依据该高程对应的平面方程计算出坝体上、下游各放样点的设计座标，再将设计座标通过平面座标平移转换成控制座标，这些可通过内业完成。值得注意的是，坝体各层设计座标仅对应于各层设计座标原点O，而各层设计座标原点O在控制座标系中所处的位置是变化的，它将由坝体立面轴线方程来决定。

从图1可以看出，测站A、B和被测点J为一任意三角形，其中测站A、B属定点，其座标为已知，被测点J座标及该点所对应的中心角为变量，根据坝体的立面轴线方程和平面轴线方程，通过内业计算提供。有 A、B、J三点座标（xa、ya）、（xb、yb）、（xj、yj），利用两点间距离方程和余弦定理，可计算出三角形ABJ的各内角。根据控制放样需要，以AB或BA为基线，仅需计算∠A和∠B。

双曲拱坝的上、下游坝面是变化的，在某一部位可能出现倒悬，放样交汇点就不能落在下层坝面（悬空），为此建议将被测点沿径向向坝内平移适当距离Δ1（JJ′，本文为0.2m），进行控制放样，见径向平移示意图（见图2），施工时自控制点沿径向向坝外平移适当距离即可。

图2 径向平移示意图

3.现场计算

在施工放样中，任何一层放样点数量都比较多，虽内业计算提供了各放样点的座标，此仅为变量，需通过计算方可求得其相应交汇角度，为避免较为繁杂现场计算，可利用具有编程功能的袖珍计算器化繁为简（本文以CASIO—f x—3800P型袖珍计算器为例）。

图1的程序为：M ODE 4

此程序启动后，只需输入坝体被测点座标（xj、yj）即可算出其相应的∠A、∠B，由于经纬仪逆时针转动时水平读盘读数减少，为避免放样时现场角度计算，故程序中又对左角（∠B）进行了数字处理，即∠B′=360-∠B，这样以AB为基线，经纬仪归零后可直接按∠A、∠B′值交汇。

程序运行

图2的程序为：M ODE4

程序中虽已考虑被测点已向坝内推移Δ1（Δ1 2=Δx2+Δy2），变量xj、yj、θj仍为推移前的相应值，但需注意 Δx（0.2×si nθ）、Δy（0.2×cosθ）前面的“+”、“-”号的变化。

程序运行

本程序参照CASIO—f x—3800P型袖珍计算器，程序中M ODE、SH IFT、ENT、H LT和RTN分别为功能转换键、第二功能键、暂停键、显示键和循环键；ki n、M i n 均为存贮键；kout、M R 均为取存键；“X2”为平方键；“”为开平方键；“±”为正、负号键；（°′″）为角度键；“”为与M ODE联合使用的小数点键，意为编程结束；程序运行中RUT为运行命令。

4.结论

拱坝建设过程中，施工放样是保证工程质量的重要环节，在笔者主持的几座拱坝工程施工中，采用上述方法进行放样和控制，均取得了满意的结果，建成后的坝体轮廓流畅，造型美观，完全满足设计要求。这种方法不需要高深的理论和先进的设备，操作简单，易于掌握，避免了繁杂的计算，对中、小型拱坝工程建设非常适用。