复合材料层合板应力分析的小波有限元法*

彭惠芬 孟广伟 范森 周立明

(1.吉林大学机械科学与工程学院，吉林长春130022;2.东北石油大学机械科学与工程学院，黑龙江大庆163318;3.东北石油大学石油工程学院，黑龙江大庆163318)

近十年来，随着复合材料层合板在航空、航天、船舶、建筑等领域广泛应用，复合材料层合板有限元分析越来越受到工程界、学术界的广泛重视.由于复合材料层合板具有拉－剪、弯－扭和拉剪－弯扭耦合效应，并且在板边缘附近应力分布复杂、变化梯度大，给传统有限元网格的划分和高精度单元的建立带来很大困难［1-4］.小波有限元是近年来发展起来的一种新型数值分析方法，已广泛应用于故障诊断、振动分析、热传导、电磁场等各个工程领域.以小波函数或尺度函数替代传统多项式插值，是优于单元网格加密和阶次升高的自适应算法［5-6］.目前，小波有限元研究的热点是如何构造精度高、稳定性好的小波单元以满足各类工程需要，为此，许多学者开展了相关方面的研究，周又和等［7］利用Daubechies小波，构造了小波梁单元和板单元;向家伟等［8］构造了区间B样条小波单元;Phoon等［9］构造了一类用于求解大梯度问题的小波单元;然而，这些小波单元绝大部分适用于各向同性材料的静动力学分析.

文中基于层合板理论，利用样条函数待定系数少、连续性强、逼近精度和计算效率高的优点［10］，采用同尺度不同阶数区间B样条小波(BSWI)尺度函数张量积对层合板位移和挠度插值，构造了BSWI二维C0型和C1型单元转换矩阵，将小波系数转化为节点物理空间自由度，并从虚功原理出发，推导了BSWI层合板单元的单元刚度方程.

1 BSWI层合板单元转换矩阵

基于经典层合板理论，在单元的交界面上需同时满足位移u、v，挠度w及其导数的兼容性和连续性.文中采用同尺度不同阶数的BSWI尺度函数张量积插值，构造层合板单元转换矩阵，单元节点及自由度排列如图1所示.

单元长度分别为 lex、ley，单元节点数为 n×n(n=2j+1，j为BSWI尺度函数的尺度)，单元总自由度数为3n2+4n+4，单元节点自由度具体布置如下:编号为1、n、n2－n+1、n2的4 个角节点自由度为 ui、vi、wi、∂wi/∂x、∂wi/∂y、∂2wi/∂x∂y;左、右边上内部节点自由度为:ui、vi、wi、∂wi/∂y;上、下边上内部节点自由度为:ui、vi、wi、∂wi/∂x;其他为内部节点，自由度为:ui、vi、wi.其中，ui、vi、wi分别为第 i个节点沿坐标轴x、y、z方向位移.

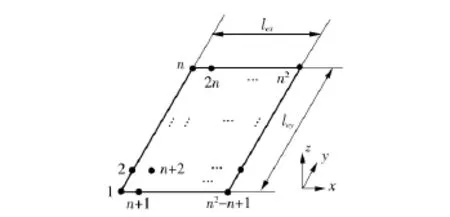
图1 小波单元节点布置Fig.1 Node distribution of wavelet finite element

采用BSWI尺度函数二维张量积插值，在单元边界节点上对未知场函数 u0(ξ，η)、v0(ξ，η)进行插值，构造二维C0型单元转换矩阵;同时对未知场函数w(ξ，η)及其导数进行插值，构造二维C1型单元转换矩阵.未知场函数可表示为

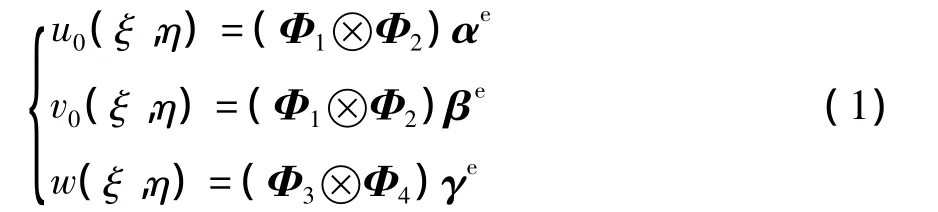
式中:u0(ξ，η)，v0(ξ，η)表示层合板中面沿 x、y 方向位移;w(ξ，η)表示层合板挠度 ;ξ、η为单元局部坐标，表示为:ξ=(x－x1)/lex、η =(y－y1)/ley，其中x1、y1为整体坐标下单元起始坐标;Φ1、Φ2和 Φ3、Φ4分别是同尺度不同阶数的一维区间B样条尺度函数，即

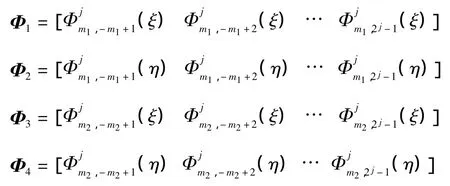
αe、βe、γe为单元上待求的小波插值系数列向量，分别表示为

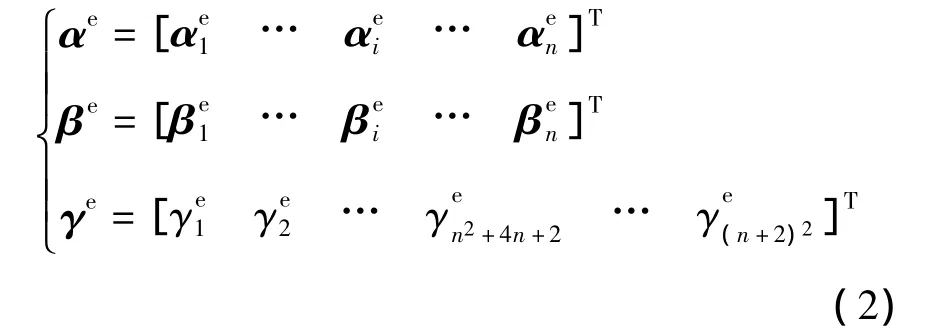
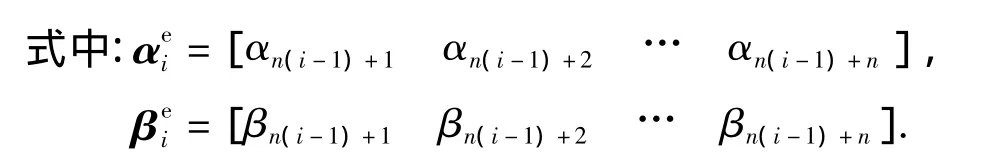
定义单元节点位移列阵:

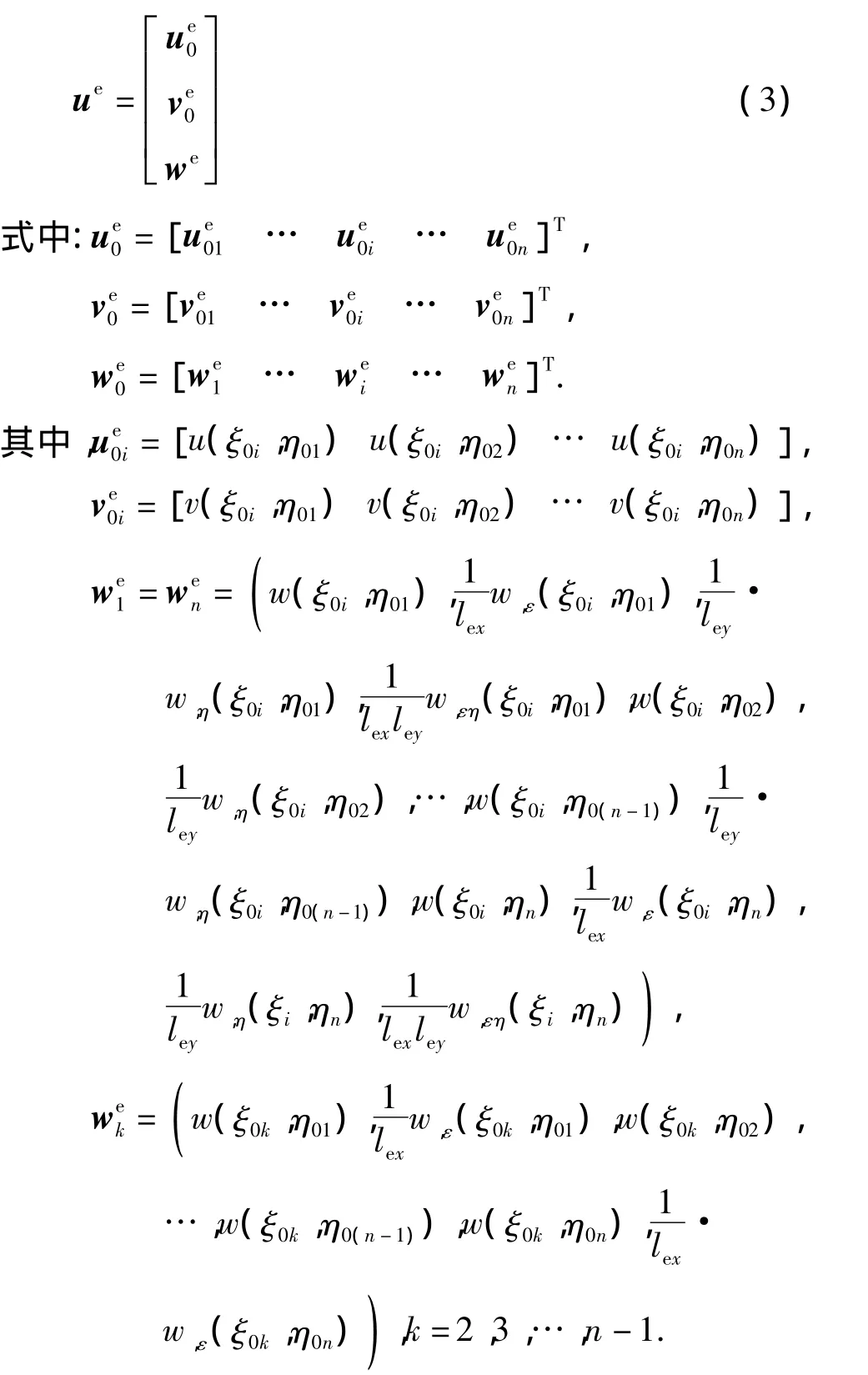
将式(3)代入式(1)得到由节点位移表示的未知场函数:

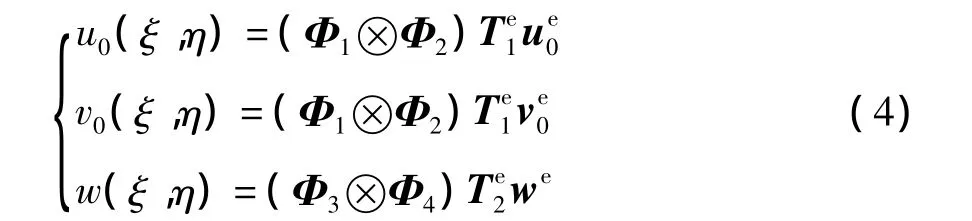
式中，C0型单元转换矩阵为C1型单元转换矩阵表示为其中:

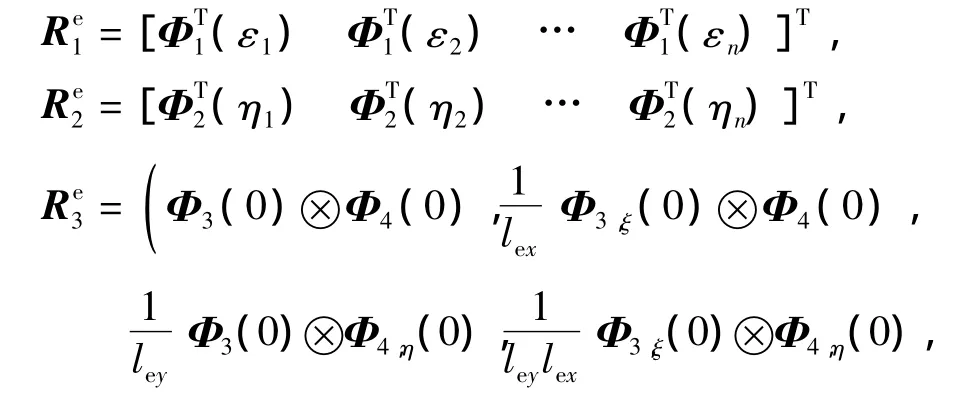
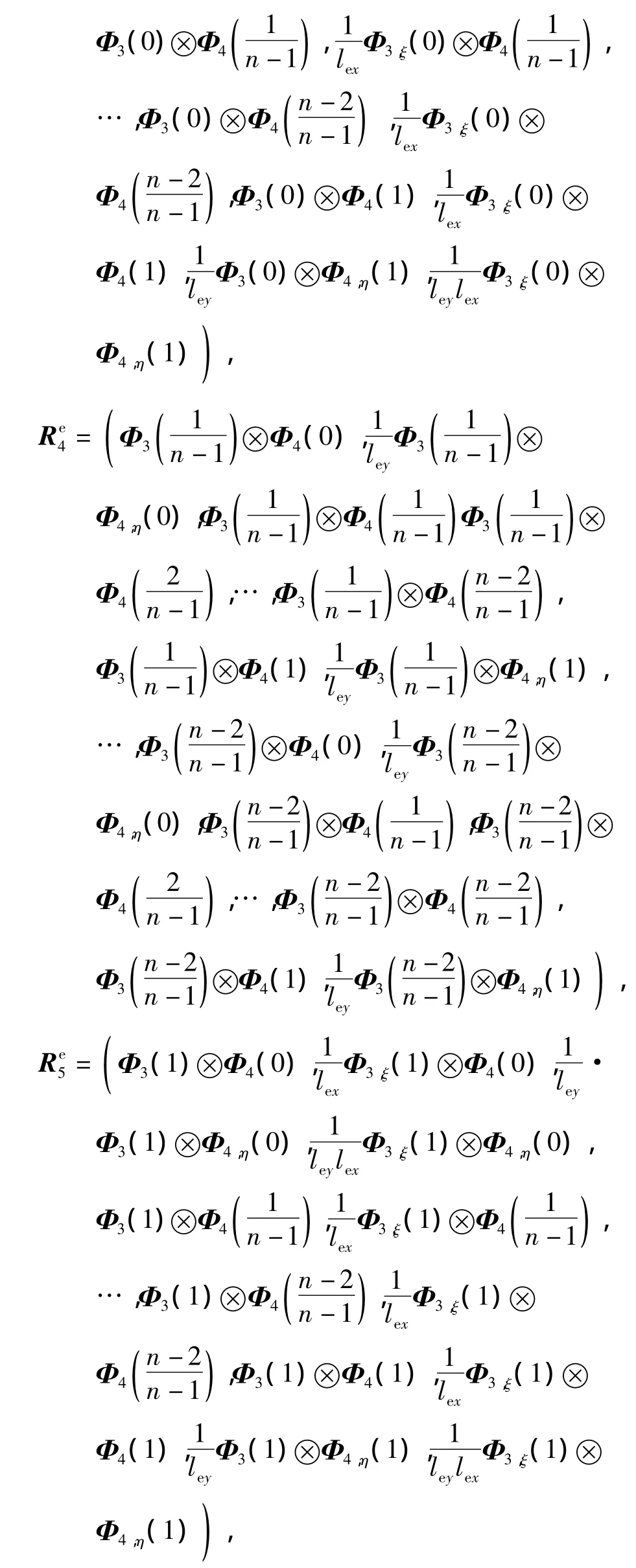
式中，Φs，m(i)表示BSWI尺度函数Φs对m偏导数在相应点i处的取值.其中

2 BSWI复合材料层合板单元构造

根据层合板理论［11-16］，取其中面为参考面，忽略厚度方向的变形(εz=0)，根据小变形假设，层合板的位移－应变关系可表示为

地产是指土地、建筑物及固着在土地、建筑物上不可分离的部分及其附带的各种权益。地产可以分为一线、二线、三四线等；

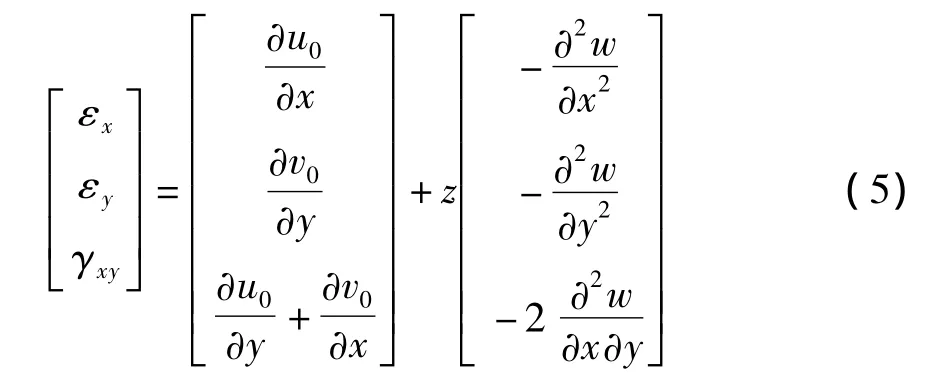
式中:u0、v0和w分别为中面沿x、y和z轴方向的位移分量;z为距中面位移;εx、εy和 γxy分别为沿 x、y和z轴方向的应变分量.

由于层合板各层刚度及材料主方向的不同，第k层应力－应变关系可表示为

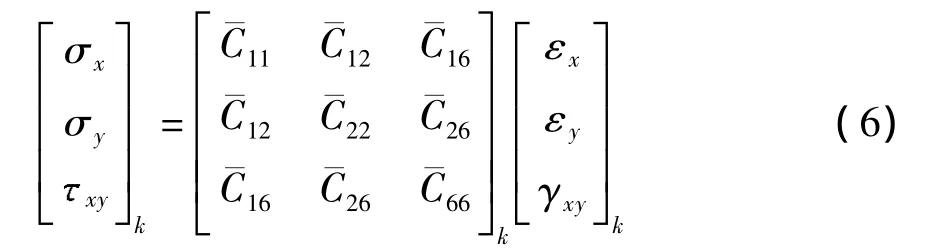
式中，

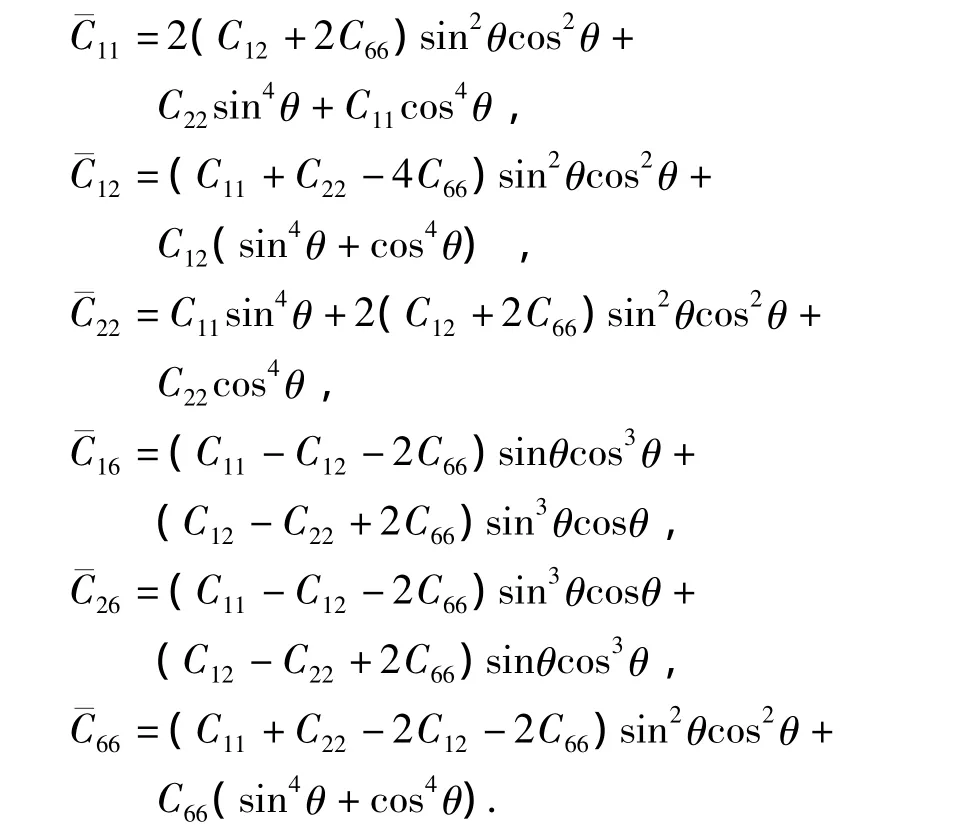
其中:θ表示从 x轴转向主轴的角度;C11=E1和E2分别为材料在1、2主方向上的弹性模量，υ12和 υ21为泊松比.

当层合板在外力作用下处于平衡时，且产生符合约束的微小虚位移，则第k层的虚功方程为

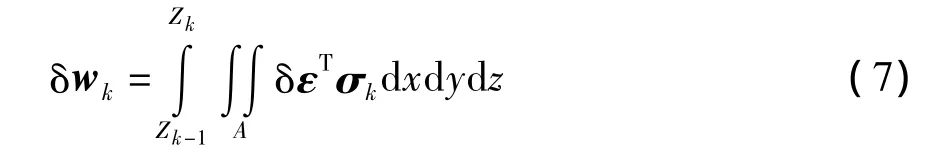
式中:虚应变列阵 δε =［δεxδεyδγxy］T，应力列阵 σk=［σxσyxy］T.

由于层合板应力的不连续分布，对所铺层求和后，可得层合板总虚功为

定义单元等效节点力列阵:

式中:

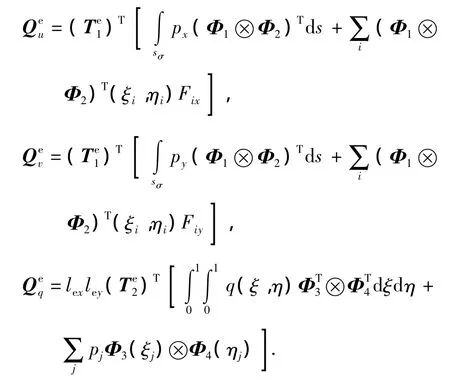
其中，面力px和py分别为层合板x、y方向轴向拉力，q为垂直于层合板面的压力，pj为集中载荷.

外力在虚位移上所作的虚功为

将式(7)－(10)联立，并将局部坐标下单元求解域 Ωs={ξ，η|ξ，η∈［0，1］}映射为整体坐标下标准求解域 Ωe，由虚功原理可得层合板 BSWI刚度方程:

3 算例分析

为验证文中构造的BSWI层合板单元的正确性和有效性，图2给出了16层等厚层合板结构示意图.层合板由上、下8层材料主方向与坐标轴夹角分别为－45°和 45°层合板组成，简记为 －45°8/45°8，单层板板厚t=0.125mm，长度a=1m，宽度b=0.5m，E1=181.00GPa，E2=10.30 GPa，v21=0.28，G12=7.17GPa，在其两侧承受轴向载荷px=5×103N/m.求:

1)对角线OA上各点挠度随距离的变化;

2)层合板应力、应变沿板厚的分布规律.

图2 层合板结构示意图Fig.2 Structure diagram of laminated composite plates

采用阶数m=2，尺度 j=3和阶数 m=4，尺度j=3的BSWI尺度函数(分别简记为 BSWI23和BSWI43)的张量积对板中面位移及挠度插值，构造BSWI层合板单元，单元数量为1个，总自由度数为283个.

表1中给出了层合板承受单向轴向拉伸时，分别采用BSWI小波有限元法和ANSYS数值分析法求解层合板1层、8(+45°)层和16层应力值，并将BSWI法与解析解进行误差比较.由表中结果可见:BSWI法计算精度明显高于ANSYS数值分析法，且BSWI法计算层合板最大应力的相对误差不超过5.03%，说明文中所构造的BSWI层合板单元是正确可行的，同时也说明本文所构造的BSWI层合板单元继承了样条函数逼近精度高，连续性强的优点，可用较少单元和自由度数获得较高的计算精度.

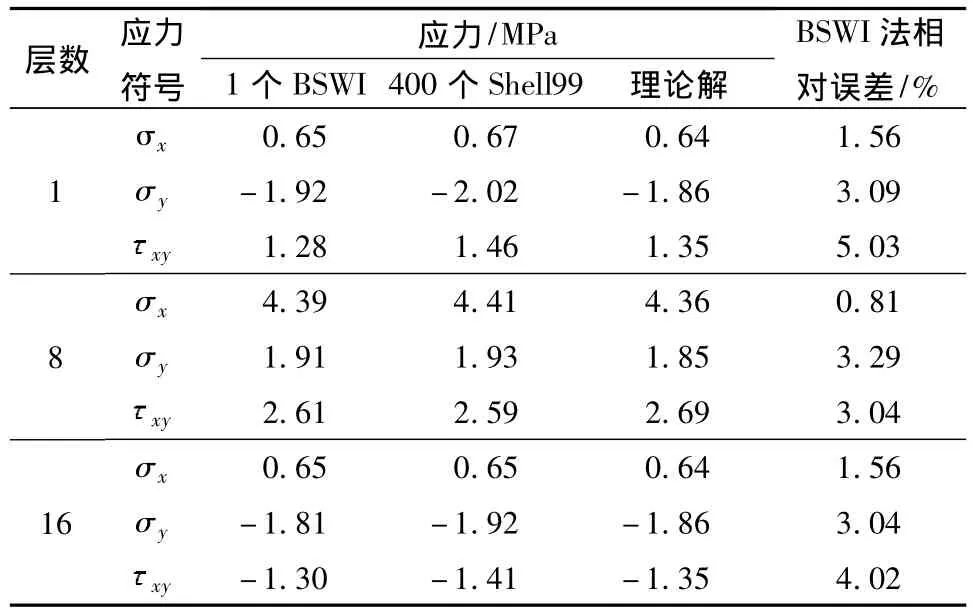
表1 BSWI法求解各层应力值与解析解比较Table 1 Comparison of analytical results of stress with those obtained by BSWI method

图3为对角线OA上各点挠度随距O点距离的变化.由图可见，由于具有拉剪耦合效应，在均匀轴向拉伸载荷作用下，非对称层合板发生了弯曲，挠度随板面上距O点距离非线性变化.其中，O点挠度为0，4个角点挠度最大为5.42 mm.图4为层合板各层应力、应变沿板厚的分布图，由图可见，层合板应变沿厚度连续分布，而各层应力不连续分布，这主要由于层合板各层刚度不同造成的.

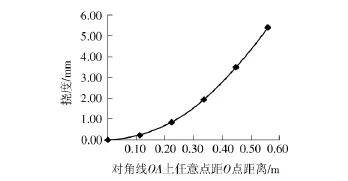
图3 对角线OA上点的挠度与距离的变化关系Fig.3 Relationship between deflection of nodes on diagonal OA and the distance to the center of plate

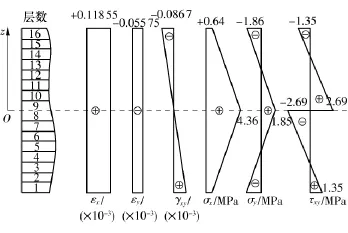
图4 层合板应变、应力沿板厚分布图Fig.4 Distributions of stress and strain of laminated composite plates in thickness direction

4 结论

文中基于经典层合板理论，采用同尺度不同阶数区间B样条小波尺度函数的二维张量积插值，构造二维C0型和C1型层合板单元转换矩阵，从而将无明确物理意义的小波系数转换为节点位移坐标，方便了相邻单元的连接和边界条件的处理，并利用虚位移原理得到了BSWI层合板单元的单元刚度方程.数值算例表明，文中构造的BSWI层合板单元在薄板的静态分析中，具有求解精度高、所用单元和自由度数量少的优点，为进行较复杂层合板结构分析提供了高精度单元.

［1］Lee Sang-Ho，Yoon Young-Cheol.Numerical predication of crack propagation by an enhanced element-free Galerkin method ［J］.Nuclear Engineering and Design，2004(3):257-271.

［2］Metin Aydogdu.A new shear deformation theory for laminated composite plates ［J］.Composite Structures，2009(89):94-101.

［3］Ferreira A J M.A formulation of the multiquadric radial basis function method for the analysis of laminated composite plates［J］.Composite Structures，2003(59):385-392.

［4］王勖成.有限单元法［M］.北京:清华大学出版社，2002.

［5］何正嘉，陈雪峰.小波有限元理论研究与工程应用的进展 ［J］.机械工程学报，2005，41(3):1-11.He Zheng-jia，Chen Xue-feng.Advanced in theory study and engineering application of wavelet finite element［J］.Chinese Journal of Mechanical Engineering，2005，41(3):1-11.

［6］Kim Y Y，Jang G W.Hat interpolation wavelet-based multi-scale Galerkin method for thin-walled box beam analysis［J］.International Journal for Numerical Methods in Engineering，2002，53:1575-1592.

［7］周又和，王记增，郑晓静.小波伽辽金有限元法在梁板结构中的应用 ［J］.应用数学和力学，1998，19(8):697-706.Zhou You-he，Wang Ji-zeng，Zheng Xiao-jing.Applications of wavelet Galerkin FEM to beam and plate structures［J］.Applied Mathematics and Mechanics，1998，19(8):697-706.

［8］向家伟，陈雪峰，何正嘉.区间B样条小波平面弹性及Mindlin板单元构造研究［J］.计算力学学报，2007，24(6):869-875.Xiang Jia-wei，Chen Xue-feng，He Zheng-jia.A study of the construction of wavelet-based plane elastomechanics and mindlin plate elements using B-spline wavelet on the interval［J］.Chinese Journal of Computational Mechanics，2007，24(6):869-875.

［9］Phoon K K，Huang S P，Quek S T.Implementation of Karhunen-Loeve expansion for simulation using a wavelet-Galerkin scheme［J］.Probabilistic Engineering Mechanics，2002(3):293-303.

［10］安宁刚，陈雪峰，曹巨江.样条小波有限元的算法研究及其应用［J］.陕西科技大学学报，2003，21(3):56-59.An Ning-gang，Chen Xue-feng，Cao Ju-jiang.The study and application of apline wavelets element methods［J］.Journal of Shaanxi University of Science ＆ Techonlogy，2003，21(3):56-59.

［11］舒小平，江永真，史林兴.精确的复合材料层合板有限元模型［J］.淮海工学院学报，2003，12(1):8-11.Shu Xiao-ping，Jiang Yong-zhen，Shi Lin-xing.An accurate finite element of laminated composite plates［J］.Journal of Huaihai Institute of Technology，2003，12(1):8-11.

［12］钟轶峰，余文斌.用渐近变分法对复合材料层合板简化数值建模及仿真［J］.重庆大学学报，2011，34(2):130-135.Zhong Yi-feng，Yu Wen-bin.Simplified numerical modeling and simulation of composite laminated plates by the variational asymptotic method ［J］.Journal of Chongqing University，2011，34(2):130-135.

［13］Shu X.A refined theor y of laminated shells with higherorder transverse shear deformation ［J］.Int J solids Struct，1997，34(6):673-683.

［14］Ghafoori E，Asghari M.Dynamic analysis of laminated composite plates traversed by a moving mass based on a first-order theory ［J］.Composite Structures，2010(92):1865-1876.

［15］沈观林，胡更开.复合材料力学［M］.北京:清华大学出版社，2006.

［16］张万平，张俊乾，吴坚.金属基复合材料纤维断裂脱落后的应力分析［J］.重庆大学学报，2004，27(9):119-123.Zhang Wan-ping，Zhang Jun-qian，Wu Jian.Analysis for a broken and debonging fiber in ductile matrix composites［J］.Journal of Chongqing University，2004，27(9):119-123.