沥青混合料三维离散元虚拟单轴蠕变试验*

张德育 黄晓明 高英

(东南大学交通学院，江苏南京210096)

随着公路交通量的增加和重载车辆的增多，车辙已成为沥青路面的主要病害之一，严重影响路面行车安全和舒适性，公路沥青路面的车辙已经成为人们普遍关注的问题.对于沥青混合料的永久变形性能，各国道路工作者提出了多种研究方法，其中以现象试验法最为普遍，但这种方法不仅需要消耗大量时间和成本，重复性和再现性也较差［1-2］.单轴蠕变试验作为常用的沥青混合料高温永久变形性能试验亦存在这种缺点.

沥青混合料由集料、沥青胶结料及空隙构成，集料在沥青混合料中呈现不连续的颗粒特性，空隙结构亦导致沥青混合料呈现不连续特性，因此，沥青混合料是一种多相复合材料，其材料性质较为复杂，实际的应力、应变场并不连续，集料、沥青胶结料及空隙在混合料中扮演着不同的力学角色，呈现出不均匀和离散的力学特性.长期以来，道路工程领域一直沿用连续均质的力学方法分析沥青混合料的永久变形性能并指导材料设计，这与沥青混合料的不连续特征不符，难以真实地反映沥青混合料的材料力学特性.

近年来，离散元方法逐渐被引入到沥青混合料性能分析中.离散元方法可以反映沥青混合料的不连续特性，从细观角度研究沥青混合料的永久变形性能，建立的虚拟试验的重复性和再现性好，经济方便，能够克服传统试验的不足.但在以往的研究中，几乎都是采用二维(2D)离散元模型对沥青混合料进行分析［3-8］，而二维结构与三维(3D)结构相差较大，二维离散元模型具有一定的局限性.因此，文中采用离散元软件PFC3D生成了包含集料、沥青砂浆及空隙的沥青混合料三维离散元虚拟试件，建立了沥青混合料三维离散元虚拟单轴蠕变试验，并与二维虚拟试验及室内试验结果进行了比较，验证了三维离散元虚拟试验方法的正确性.

1 三维离散元虚拟试件的建立

为了兼顾离散元模型的计算效率和沥青砂浆粘弹性参数的获取，将粒径大于1.18 mm的集料视为粗集料，粒径小于1.18 mm的细集料和沥青胶结料视为均质的沥青砂浆，因此，文中建立的沥青混合料离散元虚拟试件由集料、沥青砂浆和空隙构成.首先根据沥青混合料的油石比、空隙率及集料的级配(见表1)等计算出各档集料的体积，然后将各档集料逐次投放到由墙构成的直径为100 mm，高为150 mm的沥青混合料虚拟试件尺寸空间中，并通过循环保证生成的集料球单元不重叠.生成的具有级配特征的集料如图1所示.

表1 AC-16沥青混合料级配Table 1 Gradation of AC-16 asphalt mixture

图1 具有级配特征的集料Fig.1 Graded aggregates

待具有级配特征的集料生成后，在沥青混合料试件尺寸空间内生成148200个规则排列(每个单元与四周的6个单元相接触)且半径为1mm的离散单元(如图2所示).遍历新生成的离散单元，逐一判断新单元与原集料球单元的位置是否重叠，如重叠则将新单元视为集料单元，否则视为沥青砂浆单元，并将每个集料范围内的离散单元定义为刚性“聚粒”，以节省计算时间.判断结束后删除原有集料单元，生成如图3所示的三维沥青混合料虚拟试件.

图2 规则排列的离散单元Fig.2 Rugularly-packed discrete elements

图3 三维沥青混合料虚拟试件Fig.3 3D virtual specimen of asphalt mixture

由于空隙对沥青混合料的永久变形性能影响较大，为了在沥青混合料离散元虚拟试件中生成空隙，在沥青砂浆单元中随机删除5928个单元作为4%的空隙.三维离散元虚拟试件中的空隙分布如图4所示.由于室内试件及现场取芯试件内部空隙分布的复杂性，文中将虚拟试件内部的空隙分布视为随机分布.

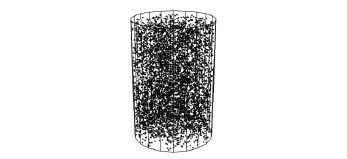
图4 沥青混合料空隙分布Fig.4 Distribution of air voids in asphalt mixture

2 微观接触模型及参数

2.1 微观接触模型

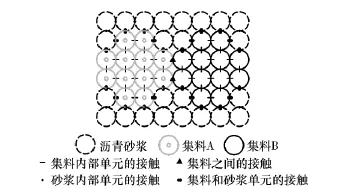
图5 沥青混合料微观组成成分的接触行为Fig.5 Interactions among microscale components in asphalt mixture

在沥青混合料离散元模型中，沥青混合料内部微观组成成分之间有4种接触，分别为集料内部单元、相邻集料之间、沥青砂浆内部单元、沥青砂浆和集料之间的接触，如图5所示.根据PFC3D中不同接触模型的特点，采用接触刚度模型描述集料内部单元之间的接触行为，采用接触刚度模型和滑移模型描述相邻集料之间的接触行为，采用伯格斯接触模型和接触粘结模型描述沥青砂浆内部单元之间以及沥青砂浆单元和集料之间的接触行为.

2.2 模型参数

PFC3D中微观接触模型的参数很难直接从室内试验得到，需要建立微观模型参数与宏观试验参数之间的关系，通过室内试验得到宏观试验参数，进而根据已建立的转化关系得到微观模型参数.

考虑到沥青砂浆的粘弹性，采用接触粘结模型和微观伯格斯接触模型(如图6所示)来描述沥青砂浆内部单元之间及沥青砂浆与集料之间的接触行为.图6 中 E1、η1、E2、η2为宏观伯格斯模型参数，Kmn、Cmn、Kkn、Ckn为微观伯格斯接触模型法向参数，Kms、Cms、Kks、Cks为微观伯格斯接触模型切向参数，m1、m2表示颗粒单元，fs为摩擦系数.

图6 伯格斯模型Fig.6 Burger’s model

由于文中主要研究沥青混合料的蠕变特性，不考虑材料的破坏，接触粘结强度取较大的值以避免单元粘结的破坏.沥青砂浆的粘弹性参数可以由DSR动态剪切试验获取，文中采用的沥青砂浆粘弹性参数分别为 E1=4.64 MPa，η1=83.34 MPa·s，E2=0.82MPa，η2=10.00 MPa·s.根据已有的研究成果［9］，微观伯格斯接触模型参数(见图6(b)和图6(c))与宏观伯格斯模型参数(见图6(a))之间的转化关系为

式中，L为相邻单元的球心距，υ为沥青砂浆泊松比.

将集料视为弹性体，采用接触刚度模型来描述集料内部单元的接触行为，采用接触刚度模型和滑动模型来描述集料之间的接触行为.由于离散单元之间的排列方式为规则的矩形排列，根据已有文献的研究成果［10］，集料的接触刚度与宏观弹性模量的转化关系为

式中:kn、ks分别为接触刚度模型的法向刚度和切向刚度;E 为集料的宏观弹性模量，文中取 55.5GPa［4，6，11］;R为集料单元的半径;υ'为集料泊松比.

3 时温等效原理

粘弹性离散元模型能够更好地模拟沥青混合料的粘弹性行为，而粘弹性模型的计算相当耗费时间［9］，以 CPU 2.8 GHz、RAM 2.0 GB 计算机进行真实时间下的虚拟试验将会花费数年的时间.因此，如果计算中采用真实加载时间，将会对虚拟试验的进行造成很大的困难，甚至无法进行.沥青混合料作为粘弹性材料，其变形依赖于时间和温度，为了减少计算时间，文中采用基于时温等效原理的方法对虚拟试验的计算效率进行优化.

时温等效原理是将材料对于外界荷载的响应进行时间和温度的等效转化，因此可以提高粘弹性材料的加载温度进而减少加载时间，再将高温下的结果通过时温等效原理向低温条件下进行转化，转化关系为

式中:ε(T，t)为真实温度T和加载时间t下的蠕变应变;ε(Tr，tr)为参考温度Tr和缩减时间tr下的蠕变应变;αT为移位因子.

在沥青混合料的研究中，时温等效原理常用来建立主曲线，进而可以将一定时间、温度范围内的试验测定结果拓延到更广泛的时间温度空间中去，大大减少材料研究中的试验工作，并在相当程度上降低对试验装置的技术要求.同样的，可以利用时温等效原理减少粘弹性离散元模型的计算时间.沥青混合料粘弹性伯格斯模型中真实温度和时间下的蠕变应变可以表达为

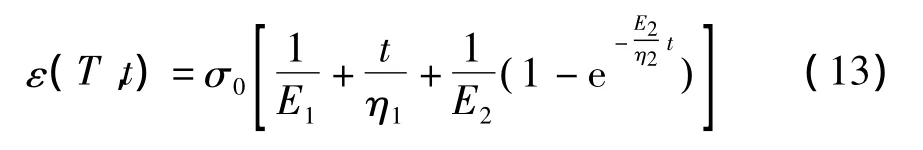
式中，σ0为轴向应力.

当温度升高到参考温度时，粘弹性参数也会随之改变.假定 E1、E2、η1r、η2r为参考温度下的伯格斯模型参数，则在缩减时间下的蠕变应变为

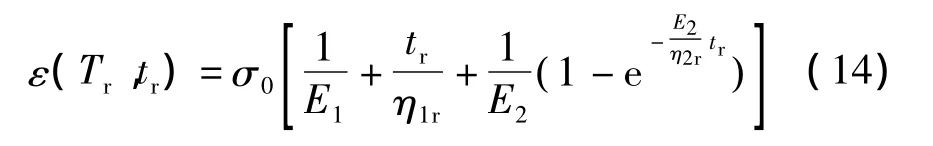
沥青混合料在真实温度和参考温度下的伯格斯模型参数是不同的，但不同温度下的蠕变应变在不同的加载时间下可以进行等效.通过求解式(11)－(14)，可以得到参考温度下的伯格斯模型参数:

在以往的文献中，离散元粘弹性模拟分析都是采用真实时间下的伯格斯模型参数，因此计算时间会很长.如果采用参考温度和缩减时间下的伯格斯模型参数，计算时间就取决于缩减时间.当移位因子取较大值时，缩减时间较真实时间大幅度缩短，因此模型的计算时间将会大大减少.经过试算，当移位因子不大于104时，计算结果较为稳定(如图7所示)，这与You等［12］的研究结论较为一致.因此，文中取104作为移位因子的取值，那么虚拟试验的加载时间仅为真实时间的1/104，计算时间从数年减少到了数天.

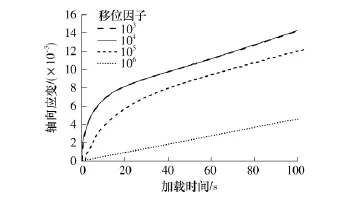
图7 不同移位因子下的沥青混合料轴向应变Fig.7 Axial strain of asphalt mixture with different shifting factors

4 虚拟单轴蠕变试验

4.1 三维虚拟试验结果

在上述建立的虚拟试件基础上，对虚拟试件施加0.7 MPa的静载.在PFC3D中，通常是通过控制墙的移动速度来对试件进行加载，因此本虚拟试验通过在试件的上下表面各设定一面墙，固定试件下表面的墙，通过PFC3D中的fish语言编写伺服控制程序，不断调整试件上表面墙的移动速度使轴向应力达到恒定的值.由于文中采用了基于时温等效的计算优化方法且移位因子取为104，当室内试验加载时间为100 s时，虚拟试验仅需加载0.01 s，计算时间大大减少.

由于沥青路面车辙通常发生在高温条件下，尤其是接近沥青软化点的时候车辙量会迅速增加［13］.因此，文中的试验温度选择具有代表性的60℃.沥青混合料试件的直径为100 mm，高为150 mm，最佳油石比为4.8%，空隙率为4%，混合料级配如表1所示.分别进行相同条件下的三维离散元虚拟试验和室内试验，并进行比较分析，结果如图8所示.

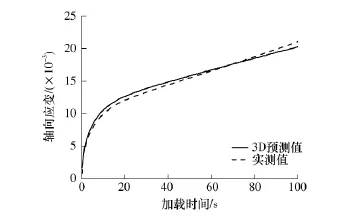
图8 三维虚拟试验与室内试验结果比较Fig.8 Comparing of results of 3D virtual test and laboratory measurement

从图8可以看出，三维离散元虚拟试验结果与真实试验的结果较为吻合，但不完全一致，其原因可能是虚拟试件中集料的形状与真实试件中集料的形状有所差别，虚拟试件内部空隙率的分布与真实试件也有所不同，而且室内试验的加载条件也没有虚拟试验理想.从总体上看，三维离散元虚拟试验能够较为准确地预估沥青混合料的永久变形性能，可以作为沥青混合料永久变形性能分析的辅助手段.

4.2 三维和二维虚拟试验结果比较

为了比较三维和二维离散元模型预估沥青混合料永久变形性能的准确性，文中还进行了相同试验条件下的二维虚拟单轴蠕变试验.二维离散元模型直接由三维离散元模型相互垂直的两个切片获得(如图9所示).三维和二维离散元模型对比结果如图10(a)所示，不同荷载下的三维和二维离散元模型对比结果如图10(b)所示.

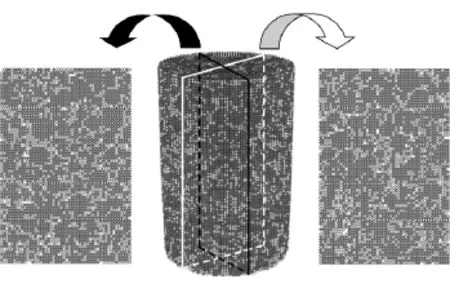
图9 沥青混合料二维离散元模型的获取Fig.9 Illustration of obtaining 2D DE model of asphalt mixture

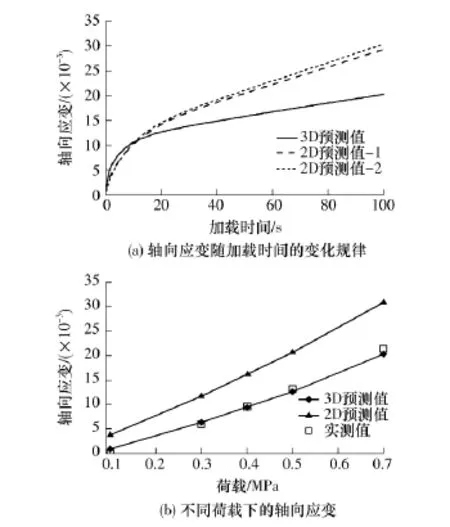
图10 三维和二维离散元模型计算结果比较Fig.10 Comparing of results of 3D and 2D DE models

从图10(a)可以看出:加载初期轴向应变的三维预测值大于二维预测值;随着加载的进行，三维预测值则小于二维预测值，且差异随之增大.从图10(b)可以看出，轴向应变的二维预测值较三维预测值及室内试验值要大，且随着荷载的增大差异也随之增大.分析其原因可能是二维模型低估了集料的嵌锁作用.三维离散元模型在预测沥青混合料高温永久变形性能方面较二维离散元模型更为理想，可以准确地预估沥青混合料的高温永久变形性能.

5 结语

文中建立了包括沥青混合料三维离散元虚拟试件的生成、沥青混合料微观组成成分微观接触模型的选取、微观接触模型参数的获取以及加载方式的实现等在内的完整的沥青混合料三维虚拟单轴蠕变试验方法，提出了基于时温等效原理的离散元粘弹性模型计算优化方法，将沥青混合料粘弹性离散元模型的计算时间从数年减少到了数天，从而解决了三维离散元粘弹性模型的计算时间问题.

二维虚拟试验结果大于三维虚拟试验及室内试验结果，且随着荷载的增大差异也随之增大，说明三维离散元模型在预测沥青混合料高温永久变形性能方面较二维离散元模型更为理想，所建立的沥青混合料三维离散元虚拟单轴蠕变试验能够准确地预估沥青混合料高温永久变形性能，可以作为沥青混合料永久变形性能分析的辅助手段.

［1］谭积青.粗集料形态与沥青混合料级配组成虚拟力学试验的基础方法研究［D］.广州:华南理工大学土木与交通学院，2006.

［2］胡霞光.沥青混合料微观力学分析综述［J］.长安大学学报:自然科学版，2005，25(2):6-9.Hu Xia-guang.Review on asphalt mixture micromechanics analysis［J］.Journal of Chang＇an University:Natural Science Edition，2005，25(2):6-9.

［3］Chang G K，Meegoda J N.Micromechanical simulation of hot mix asphalt［J］.Journal of Engineering Mechanics，1997，123(5):495-503.

［4］Buttlar W G，You Z P.Discrete element modeling of asphalt concrete:microfabric approach ［J］.Transportation Research Record，2001，1757:111-118.

［5］王端宜，张肖宁，王绍怀.用虚拟试验方法评价沥青混合料的级配类型［J］.华南理工大学学报:自然科学版，2003，31(2):48-51.Wang Duan-yi，Zhang Xiao-ning，Wang Shao-huai.Evaluation on grading type of asphalt mixture with virtual test method［J］.Journal of South China University of Technology:Natural Science Edition，2003，31(2):48-51.

［6］You Z P，Buttlar W G.Discrete element modeling to predict the modulus of asphalt concrete mixtures［J］.Journal of Materials in Civil Engineering，2004，16(2):140-146.

［7］Abbas A，Masad E，Paapagiannakis T，et al.Micromechanical modeling of the viscoelastic behavior of asphalt mixtures using the discrete element method［J］.International Journal of Geomechanics，2007，7(2):131-139.

［8］Kim H，Wagoner W P，Buttlar W G.Simulation of fracture behavior in asphalt concrete using a heterogeneous cohesive zone discrete element model［J］.Journal of Materials in Civil Engineering，2008，20(8):552-563.

［9］Liu Y，Dai Q L，You Z P.Viscoelastic model for discrete element simulation of asphalt mixtures［J］.Journal of Engineering Mechanics，2009，135(4):324-333.

［10］Thornton C.The conditions for failure of a face-centered cubic array of uniform rigid spheres［J］.Geotechnique，1979，29(4):441-459.

［11］You Z P.Development of a micromechanical modeling approach to predict asphalt mixture stiffness using the discrete element method［D］.Urbana-Champaign:Department of Civil and Environmental Engineering，University of Illinois at Urbana-Champaign，2003.

［12］You Z P，Liu Y，Dai Q L.Three-dimensional microstructural-based discrete element viscoelastic modeling of creep compliance tests for asphalt mixtures［J］.Journal of Materials in Civil Engineering，2011，23(1):79-87.

［13］黄晓明，范跃武，赵永利，等.高速公路沥青路面高温车辙的调查与分析［J］.公路交通科技，2007，24(5):16-20.Huang Xiao-ming，Fan Yue-wu，Zhao Yong-li，et al.Investigation and test of expressway asphalt pavement hightemperature performance［J］.Journal of Highway and Transportation Research and Development，2007，24(5):16-20.