一种高效的RC－LDPC编码IR－HARQ方案

陈 翔，姜 晖

(合肥电子工程学院，安徽 合肥 230037)

低密度奇偶校验(LDPC)码是R.G.Gallager在1962年提出的［1］，自从其接近香农限的性能于1996年被Mackay等人重新认识以来［2］，迅速成为信道编码领域研究的热点。与Turbo码一样，LDPC码的卓越性能源自其随机化编码思想和迭代译码思想。而校验矩阵有双对角线结构的LDPC码能实现线性复杂度的编译码器，具有很高的实用价值［3－4］。目前，美国国家航空和宇航局(NASA)已经将LDPC码作为近地和深空通信的首选［5］。此外，LDPC码在无线局域网(WLAN)、无线城域网(WiMAX)、欧洲第二代卫星数字视频广播(DVB－S2)等民用领域也得到了广泛应用。

复杂信号环境下的无线信道状况是实时变化的，第一次传输常常因为信道估计的误差而不能达到系统的可靠性要求。增余型混合自动重传请求(IR－HARQ)技术将信道编码和反馈重传相结合，根据反馈的第一次传输的误码率情况，发送端在第一次传输所用的纠错码码字后增加一定数量的新校验码元，将新校验码元调制后发送到接收端，接收端解调后与第一次传输的码字合并译码，这等效于降低了纠错码的码率，提高了译码成功的概率，以满足系统可靠性要求。

本文针对提高IR－HARQ系统频谱有效性这一问题，首先构造了码率间隔足够细、码率范围足够大的速率匹配码族，这样重传时才有选择合适数量的新校验码元的余地;然后基于互信息(MI)模型进行链路自适应设计，根据第一次传输的误码率情况，准确预测出最少重传的新校验码元数(或调制符号数)，即可满足系统的可靠性要求，使系统在传输有效信息时占用的无线资源最少。

1 RC－LDPC码设计

速率匹配的卷积码和RC－Turbo码族的设计一般是这样:首先设计一个码率较低(如1/3)的母码，再对母码进行删余(puncturing)得到高码率码字。只要删余图样设计得合适，就能得到码率间隔足够细，且性能很好的速率匹配卷积码和RC－Turbo码族。而LDPC码设计的基础是稀疏校验矩阵，这使得RC－LDPC码族的设计相对复杂。因为每一次删余操作都会引起校验矩阵结构的变化，改变LDPC码的次数分布对，因此删余的码率跨度不宜过大，为此，一般选择码率中等的LDPC码作为母码，这样，低码率的码字只能通过对母码校验矩阵进行嵌套的扩展得到。

在之前的工作中，以IEEE802.16e标准［6］规定的码率为1/2的LDPC码为母码，根据其分块LDPC码的特点，经过对多种速率匹配算法的考察比较，选择了复杂度与性能俱佳的校验矩阵扩展算法、基于块恢复树的删余算法和块删余算法，构造出一组码率范围从0.1到0.9、码率间隔为0.1的 RC－LDPC码族［7］，如表1所列。在RC－LDPC编码的自适应IR－HARQ系统中，继续使用该LDPC码族。

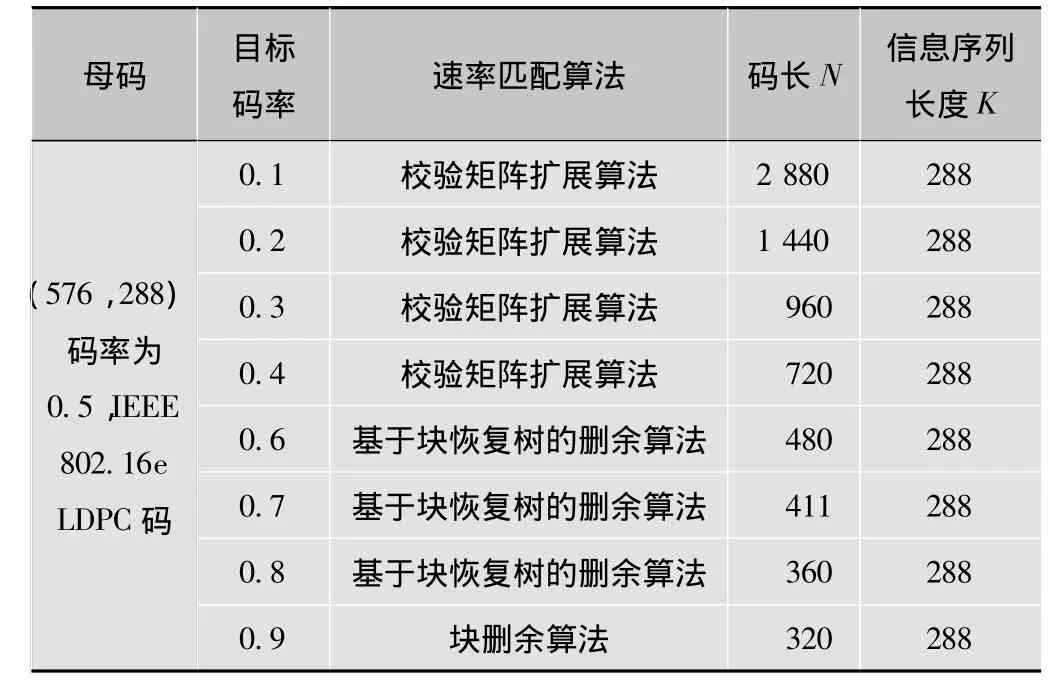
表1 码率范围从0.1到0.9，码率间隔为0.1的RC－LDPC码族的构造

2 以互信息模型为基础的链路自适应设计

为了使信息传输效率最大化，IR－HARQ方案的实际误码率应始终保持在略低于系统要求的误码率指标的水平上。在所设计的RC－LDPC码族的调制编码方案(MCS)集合中，为了选择最适合当前信道状态的MCS，需要通过链路级仿真得到所有这些MCS在不同衰落情况下的链路级性能曲线，其工作量是巨大的。若有了合适的LEP模型，则通过其中一些MCS在AWGN信道下的链路级性能曲线就能足够精确地预测其他MCS在不同衰落情况下的瞬时性能，这对降低系统复杂度有重要意义。

传统的单载波LEP模型不适用于像正交频分复用(OFDM)这样的多载波系统，因为在频域有着明显的信道变化，两个平均信干噪比(SINR)完全相等的链路误码率性能可能差别很大，因此，能由瞬时的信道衰落样式(fading profile)准确预测出瞬时误码率的LEP模型才适用于多载波系统，互信息(MI)模型正是这样一种模型。

MI模型是Lei Wan等人于2006年提出的，它对Turbo/卷积编码的多载波系统都有很好的精确度［8］。随后，本文证明了MI模型同样适用于RC－LDPC编码的多载波系统［7］。MI模型通过互信息计算将多载波系统每个子载波上的SINR构成的向量映射为一个标量RBIR，再由RBIR预测误码率，它分为调制模型和编码模型两个子模型，其原理框图如图1所示。

2.1 调制模型

MI模型假设在一定的传输时间间隔(TTI)内，多载波/多天线系统各个子信道的信道状态不发生变化。调制模型中SINR1，SINR2，…，SINRJ是一个TTI内各个子信道经历的信道状态。每个子信道采用的调制方式可能不同，但从译码器的角度看，每个子信道的输出是各个解调器的软输出携带的互信息，它是基于信道互信息的信息度量，即调制符号互信息(SI)，表示为

图1 互信息(MI)模型的原理框图

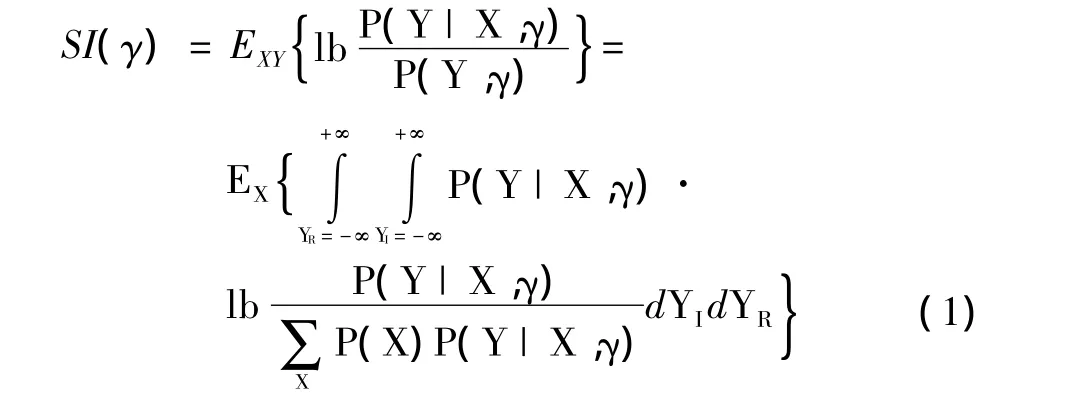
式中:γ=Es/N0表示调制符号X经历的信道状态，P(X)是X 的先验信息，Y=YR+i×YI是接收的符号，P(Y|X，γ)是Y在信干噪比γ下的条件概率密度函数。式(1)表明SI代表的是离散输入连续输出信道的容量。

2.2 编码模型

编码模型包括SI收集单元和链路质量映射单元。SI收集单元将调制模型输出的SI累加起来得到已接收编码比特互信息(RBI)，并对其进行归一化，得到每个编码比特的互信息，即已接收编码比特信息率(RBIR)，显然，RBIR的取值范围是0到1。

式中:J表示子载波个数，γj表示第j个子载波的信噪比状态，mj表示第j个子载波的调制阶数，N表示码长。RBIR是互信息模型中很关键的量，链路质量映射单元根据RBIR值查表得到与最初的瞬时SNIR向量对应的瞬时误码率(BLEP)。

2.3 MI模型的两个查找表

MI模型基于两个查找表进行自适应IR－HARQ设计:查找表A是各种码率LDPC码编码的单载波系统在AWGN信道、BPSK调制条件下仿真得到的BLER－RBIR查找表，如表2所示。显然，每一个BLEP的自然对数值在每种码率下都对应了一个RBIR值，表中未列出的BLEP值或更精细的码率对应的RBIR值可以通过线性内插得到，这也是存储BLEP的自然对数值的目的。查找表B是RBIR－SINR查找表，如图2所示，用于代替式(1)的互信息计算、式(2)的互信息累加，以及式(3)的互信息归一化。

表2 MI模型的查找表A:BLER－RBIR查找表

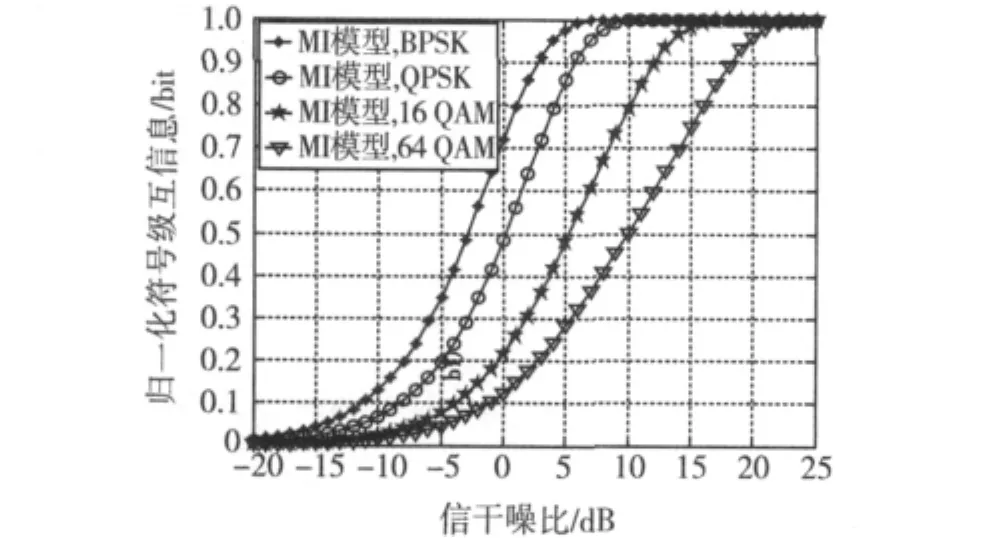
图2 MI模型的查找表B:RBIR－SINR查找表

3 自适应IR－HARQ方案

基于MI模型的RC－LDPC编码自适应IR－HARQ方案如图3所示，初始传输的码长为N，重传时发送T个新的校验码元，两次传输的信道状态不同，分别为SINR1和SINR2。若两次传输的调制方式不同，可通过MI模型的查找表B，以RBIR为中间量将SINR1和SINR2映射为BPSK 调制下的等效信干噪比 SINRBPSK，1和 SINRBPSK，2，那么两次传输等效为一次传输，数据块长度为N+T，采用BPSK调制方式，数据块经历了两种信道状态:SINRBPSK，1和 SINRBPSK，2。

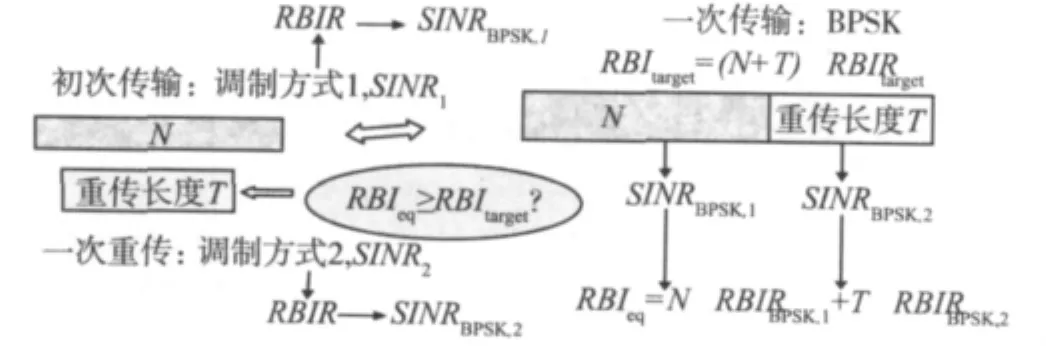
图3 基于MI模型的自适应IR－HARQ原理图

IR－HARQ方案通过搜索得到最优重传码元数T，搜索的过程以MI模型的两个查找表为基础，流程如图4所示，初始传输译码失败才需要重传，重传码元数T从零开始逐符号地增加，重传后的等效码率为

式中:R0是初始传输的码率。由等效码率R在MI模型的查找表A中找到与系统误码率要求BLEPtarget对应的RBIRtarget，从而算得满足系统误码率要求的编码比特信息量

图4 基于MI模型的自适应增余型HARQ方案的重传码元数预测流程图

再由 2次传输的等效信道状态 SINRBPSK，1和SINRBPSK，2，在MI模型的查找表B中找到对应的编码比特互信息率 RBIRBPSK，1和 RBIRBPSK，2，由式(3)计算2 次传输的总信息量

如果RBIeq≥RBItarget，那么译码成功的概率肯定大于BLEPtarget，从而满足系统的误码率要求，此时T的值就是预测的最佳重传码元数。如果RBIeq＜RBItarget，那么继续逐符号地增加重传码元数，直到RBIeq≥RBItarget或已达系统所支持的最低码率为止。

4 仿真结果和分析

为了验证上述自适应IR－HARQ方案的正确性，建立了最大重传次数为1的链路级平台进行仿真验证。初次传输使用的MCS是(320，288)RC－LDPC码与64QAM调制结合，这是MCS集合中最高码率0.9和最高阶调制方式的组合，重传时改用BPSK调制方式，设定系统要求误块率不高于1%，即BLERtarget=0.01，仿真信道为单径Rayleigh块衰落信道，理想信道估计，即2次传输的SINR值收发端都已知，误块率采用短时统计。由于系统支持的最低码率是0.1，即 (2880 ，288)RC－LDPC 码，因此最大重传符号数Tmax=2560 。

图5给出了自适应IR－HARQ方案的瞬时误块率曲线，横坐标的有效信噪比是2次传输都等效为使用BPSK调制时的信噪比。图6和图7分别给出了相应的重传符号数和等效码率曲线。

可以看出，自适应IR－HARQ方案的瞬时误块率曲线分为3段:当信噪比从－8 dB变化到－7 dB时，系统误块率从1下降到1%，对应的重传符号数为Tmax=2560 ，意味着信噪比低于－7 dB时，重传采用的是稳健性最强的码率为0.1的LDPC和BPSK的组合，但仍无法满足系统误码率要求，需要多次重传，配合包合并方案进一步提高性能;当信噪比从－7 dB变化到5 dB时，系统误块率保持在等于1%或略低于1%的水平，而相应的重传符号数逐渐从Tmax=2560 下降到0，意味着MI模型正确预测了最少应重传的符号数，使系统在恰好满足误码率要求的前提下，最大限度地减少了无线资源的使用;当信噪比高于5 dB时，系统采用0.9码率进行传输，无需重传就已经满足误码率要求了。从图5中可以看出，实际仿真得到的BLEP曲线略低于MI模型预测的BLEP曲线。这是因为，查找表A中码率以0.1为间隔、BLEP的自然对数值也以0.1为间隔，其余码率和BLEP值对应的RBIR值都是通过线性内插得到，这样会引入一些误差，因为BLER和码率之间并不是线性的关系，但这样近似已经比较精确了，实际误码率保持在略低于目标误码率的水平上。总之，MI模型准确预测了自适应IR－HARQ方案的最优重传符号数。

5 小结

理论分析和仿真验证表明，基于MI模型的能准确预测RC－LDPC编码的自适应IR－HARQ系统的最优重传符号数，允许每次传输根据信道状况采用不同的调制方式，且有很大的码率跨度范围，在很宽的信噪比范围内实现了“在恰好满足系统误码率要求的前提下，最大限度节约无线资源”的目标。

［1］GALLAGER R.Low－density parity－check codes［J］.IRE Transactions on Information Theory，1962，8(1):21－28.

［2］MACKAY D J C，NEAL R M.Near shannon limit performance of low density parity check codes ［J］.Electronics Letters，1997，33(6):457－458.

［3］龚昊，龙沪强，张罗鸣，等.一种低误码平层的LDPC码的构造与实现［J］. 电视技术，2008，32(S1):107－110.

［4］刘春江，吴智勇，于新，等.一类准循环LDPC码的快速编码方法［J］.电视技术，2007，31(6):12－14.

［5］DJORDJEVIC I B.Low density parity check codes for use in near－earth and deep space applications［C］//Proc.2011 International Conference on Space Optical Systems and applications(ICSOS).Washington DC，USA:National Aeronautics and Space Administration，2011:325－333.

［6］IEEE802.16E，IEEE standard for local and metropolitan area networks，part 16:air interface for fixed broadband wireless access systems，amendent 2:for physical and medium access control layers for combined fixed and mobile operations in licensed bands［S］.2006.

［7］CHENG Xiang，WAN Lei，GAO Zhenyuan，et al.The application of eesm and mi－based link quality models for rate compatible ldpc codes［C］//Proc.2007 VTC－2007 Fall 2007 IEEE 66th of the Vehicular Technology Conference.［S.l.］:IEEE Press，2007:1288－1292.

［8］LEI W，SHIAUHE T，ALMGREN M.A fading－insensitive performance metric for a unified link quality model［C］//Proc.WCNC 2006 IEEE Conference of the Wireless Communications and Networking.［S.l.］:IEEE Press，2006:2110－2114.