基于Contourlet变换的纺织品缺陷检测算法

施亦东，吴 炜，何国琼

(1.武汉纺织大学新型纺织材料绿色加工及其功能化教育部重点实验室，湖北 武汉 430073;2.四川大学轻纺食品学院，四川 成都 610065;3.四川大学电子信息学院，四川 成都 610065)

纺织品缺陷是指因生产过程中生产工序和工艺的差异或不稳定，在最终产品上出现的影响织物性能及外观质量的缺陷。它是纺织品质量控制的一项重要指标［1－2］。纺织品缺陷的检测就是在织造、染整完成后，在验布过程中对成品质量的评分和分级工作。其目标是及时发现在纺织品中存在的缺陷，避免不合格产品流入市场，同时对产生缺陷的原因进行分析，并及时反馈给生产部门。纺织品缺陷的检测是纺织品质量控制的关键环节。长期以来，纺织品缺陷的检测都是由人工视觉完成，这种方法存在显然的缺陷，如劳动强度大、效率低、漏检率高、受检验人员主观因素影响大，难以得到客观的检验结果。因此基于计算机视觉的纺织品缺陷检测在纺织品质量控制中的地位日益重要。随着机器视觉及相关技术的进一步发展，纺织品质量的自动检测将越来越多地应用于现代工业生产过程中。

目前纺织品缺陷检测技术可分为两大类［3］。一类是利用纺织品图像纹理的统计特性进行分析，其典型算法主要是灰度共生矩阵［4］。总体来说，这类算法存在计算量大且识别率普遍不高的缺点。另外一类是将纺织品图像变换到变换域，然后再进行分析和缺陷的检测。其典型算法主要是基于小波变换的方法。小波变换［5－8］能够更灵活地检测出纺织品图像的各个分解量，将各种交织在一起的不同频率组成的混合信号分解成不相同频率的块信号。它能有效地应用于模式识别、边缘检测等问题以及纺织品缺陷的检测。但是小波变换应用于图像处理时，一般采用可分离二维小波变换(即采用先对行做一次一维小波变换，再对列做一次一维小波变换)。这导致小波基函数的支撑区域为正方形，使其只能捕获水平、垂直和对角3个方向的信息，相对而言其基函数形状的方向性较差。

Contourlet变换［9］作为新的信号分析工具，解决了小波变换不能有效表示二维或更高维奇异性的缺点，并能准确地将图像中的边缘捕获到不同尺度、不同方向的子带中。它不仅具有小波变换的多尺度特性，还具有小波变换不具有的多方向性和各向异性，更能准确地提取图像的特征(方向)信息。这将使Contourlet变换提取的高频特征比小波变换提取的高频特征更加丰富，更有利于纺织品缺陷的检测。

笔者针对纺织品缺陷的检测提出了一种基于Contourlet变换的纺织品缺陷检测方法。该方法首先使用Contourlet对纺织品图像进行分解;然后计算变换后的Contourlet系数的统计特征;最后利用欧氏距离对Contourlet系数的统计特征进行缺陷检测。实验结果表明该算法在纺织品缺陷检测中取得了满意的检测效果。

1 Contourlet变换

Contourlet变换［9］是 M.N.Do 和 Martin Vetterti提出的一种二维图像表示方法。由于大多数自然图像并非全部由一些不连续的点组成，而是很大程度上由分段光滑的轮廓线组成。二维小波变换对零维或不连续的点有稀疏表示，而对于轮廓线的表示能力有限。Contourlet变换克服了小波变换的缺点。在Contourlet变换的过程中，首先应用拉普拉斯金字塔分级来捕获点不连续性，再利用方向滤波器将点不连续性与线结构联系起来，从而得到图像的稀疏表示，总体类似于将图像用轮廓线(Contour)分割为基本的单元。Contourlet变换在尺度、方向和方框的比例上都是弹性的。同时Contourlet在频率域提供了一个多级定向的分解，能够满足曲线的各向异性尺度关系，并提供一种快速的、结构化的分解信号方法。

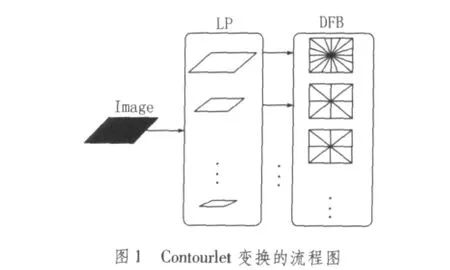
Contourlet变换由多尺度分析的拉普拉斯塔式金字塔(Laplacian Pyramid，LP)和方向分析的方向滤波器组(Directional Filter Bank，DFB)组成。Contourlet变换的步骤分为两步:1)由拉普拉斯塔式金字塔对图像进行多尺度分解以“捕获”奇异点(高频信息)，生成一个原始图像的低通采样信号(即高斯图像)和一个原始图像与预测图像之差形成的带通图像(即拉普拉斯图像);2)其中拉普拉斯塔式金字塔分解后的带通图像由方向滤波器组进行2k方向分解(其中k可自行定义，以获得期望的方向分解数)，将频域分解成2k个楔型(wedge shape)子带，使得分布在同方向上的奇异点合成为一个系数。

Coutourlet是一种多分辨力、多方向的变换。其中拉普拉斯金字塔分解实现多分辨力，而方向滤波器组实现多方向。金字塔分解不具有方向性，而方向滤波器对高频部分能很好地分解，对低频部分却不能。两者的结合恰好能弥补对方的不足，从而得到很好的图像描述方式。图1为使用拉普拉斯金字塔和方向滤波器组一起进行Contourlet变换的示意图。拉普拉斯金字塔输出的带通图像传递给方向滤波器组，当对这些带通图像应用方向滤波器组时，便能有效地“捕获”方向信息。图2a为一幅带缺陷的纺织品图像;图2b为图2a进行2层Contourlet变换，4个方向分解后的结果。从图2可以看出Contourlet变换能够有效地分解原始图像，并提取各个方向的高频特征信息。

2 统计特征

提取统计特征量［2］的目的是对Contourlet系数固有的、本质的特征和属性进行测量，并将结果数值化为特征矢量，即用一组多维矢量来表征Contourlet系数，为后续的分析提供基础。考虑到计算的简洁性，该算法选择了均值、方差、峰度(Kurtosis)、偏度(Skewness)4种特征量进行统计计算。

令P为大小为N×M的图像(系数)块。P(x，y)表示图像块P在(x，y)处的像素(系数)值。

均值表征Contourlet系数的平均强度，公式为

方差可表征Contourlet系数的变化程度，公式为

峰度(Kurtosis)为描述总体中所有取值分布形态陡缓程度的统计量，公式为

偏度(Skewness)与峰度类似，它也是描述数据分布形态的统计量，其描述的是某总体取值分布的对称性，公式为

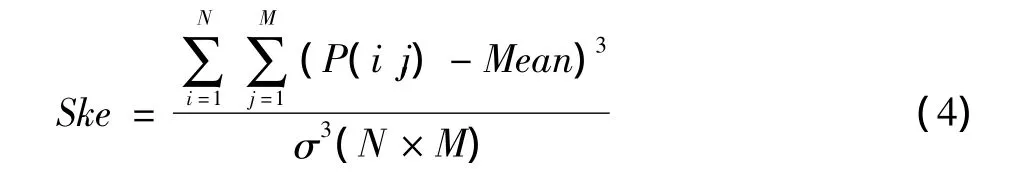
3 基于Contourlet变换系数统计特征的检测算法

纺织品缺陷检测的目标是根据纺织品图像的特性确定缺陷位置的过程。与识别问题不同，检测纺织品缺陷只需要将待检测的纺织品分为有无缺陷两类。另外，对于有缺陷的需要标明其缺陷的位置。由于缺陷的大小、形状及类型不固定，因而加剧了纺织品缺陷检测问题的复杂和困难程度。考虑到在纺织品检测过程中，有些缺陷可能从未出现过，但是当织物上面存在一些缺陷时，这些缺陷区跟周围有明显的区别。由此可以认为只要与正常的纺织品有较大差异的，都是有缺陷的纺织品。

由于在Contourlet分解域进行纹理分析可利用纹理空域、频域信息，该算法将纺织品图像通过Contourlet变换，接着将Contourlet系数划分成若干固定尺寸的系数块，然后统计Contourlet系数块的统计特征。相对来说，无缺陷纺织品可以轻易预先获取，因此可以先获取无缺陷的纺织品样本特征，并将该特征作为模板。在检测过程中，将待检测的纺织品图像同样进行Contourlet变换，获取Contourlet系数，同样将该系数划分成若干系数块。然后每一个系数块与先前建立的模板进行比较，如果差异大于预先设定的阈值，则认为是存在缺陷的纺织品图像，并标明该图像块的位置;反之，则为正常的纺织品。

整个检测过程可由两个模块组成:训练模块和检测模块。训练模块的目的是通过对正常纺织品样本进行Contourlet变换，提取其Contourlet变换后的系数的统计特征，并将该特征作为无缺陷样本的模板。检测模块的目的是将纺织品缺陷检测出来，并标明块的位置。该纺织品缺陷检测算法的训练和检测过程如图3所示。

图3 纺织品缺陷检测算法的训练和分类检测流程图

3.1 训练模块

训练模块的步骤如下:

1)对无缺陷的纺织品样本进行2层4个方向的Contourlet变换。

2)将变换后的高频信息(即Contourlet变换系数)进行分块(例如16×16)。

3)计算每个方向上的位置为 k，k=1，2，…，C(C 为分块的数目)的分块的统计特征，即均值、方差、峰度(Kurtosis)、偏度(Skewness)，并对其进行归一化处理。其中归一化使用的公式为其中x表示需要归一化的特征，MinV和MaxV分别表示需归一化的特征x的最小值和最大值。

4)将前一步计算的特征组合为一个特征向量(每个块使用4个方向×4个特征=16个特征表示)。

5)使用所有块的特征向量，构建一个无缺陷的样本模板库。

3.2 分类检测模块

分类检测模块的步骤如下:

1)对待检测的纺织品样本进行2层4个方向的Contourlet变换。

2)将变换后的高频信息进行分块。

3)计算每一位置，每个方向上分块的统计特征，即均值、方差、峰度、偏度，并对其进行归一化处理。

4)将前一步计算的特征组合为一个特征向量(这样每个块使用4个方向×4个特征=16个特征表示)。

5)将上一步计算获取的特征向量与训练过程中构建的无缺陷的样本模板库中的统计特征进行比较。如果与无缺陷的样本模板库中最相近距离(使用两个向量的欧氏距离计算)的块大于预先设定的阈值T，则认为该块存在缺陷，否则为无缺陷的块。

4 实验结果

为了验证该算法的效果，笔者对3种不同的纺织品缺陷进行了检测。部分无缺陷的纺织品图像如图4a所示，其对应的包含缺陷的纺织品图像如图4b所示。

实验中，笔者将无缺陷的纺织品图像输入训练模块进行训练，然后将带缺陷的样本输入分类检测模块进行判断。部分实验结果如图5所示，图5a为带缺陷的纺织品图像，图5b为对应的检测结果(白色表明该部分存在缺陷)。从这些检测结果图可以看出，缺陷部分被完全检测出来，从而验证了该算法的有效性。

5 结论

Contourlet变换作为一种新的信号分析工具，能准确地将图像中的边缘捕获到不同尺度、不同方向的子带中。鉴于此，本文提出了一种基于Contourlet变换的纺织品缺陷检测方法，利用Contourlet变换对纺织品图像进行分解，将Contourlet变换系数的统计特征用于缺陷的检测，实验验证了该算法的有效性。

［1］钟克洪，丁明跃，周成平.基于小波差分统计特征的纹理缺陷检测方法［J］. 系统工程与电子技术，2004，26(5):660－664.

［2］陈珂，殷国富，罗小宾.基于统计特征聚类原理的图像识别技术［J］.四川大学学报:工程科学版，2003，35(5):83－86.

［3］沈晶，杨学志.一种新的基于纹理分水岭的纺织品缺陷检测方法［J］.中国图象图形学报，2009，14(10):1997－2003.

［4］郭航，霍宏涛.灰度共生矩阵在皮肤纹理检测中的应用研究［J］.中国图象图形学报，2010，15(7):1074－1078.

［5］杨学志，沈晶.采用小波框架的纺织品缺陷分类方法［J］.工程图学学报，2009(5):108－112.

［6］SARI S H，GODDARD J S.Vision system for on－loom fabric inspection［J］.IEEE Trans.Industry Applications，1999，35(6):1252－1259.

［7］LATIF A，ERTUZUN A，ERCIL A.An efficient method for texture defect detection:sub－band domain cooccurrence matrices［J］.Image and Vision Computing，2000，18:543－553.

［8］TSAI D，HSIAO B.Automatic surface inspection using wavelet reconstruction［J］.Pattern Recognition，2001，34(6):1285－1305.

［9］DO M N，VETTERLI M.The contourlet transform:an efficient directional multiresolution image representation［J］.IEEE Trans.Image Processing，2005，14(12):2091－2106.