一种基于阶跃响应的理想频率信号源及频域分析的研究

李 军，万文军，张 曦

（广东电网公司电力科学研究院，广州510080）

控制回路或对象的频率特性是控制系统设计和参数调整的根本依据［1-2］.在工业过程中，频率响应分析法的实施受到了各种因素的限制：首先，获取频率特性便是一项极其繁杂的事情，有时工艺过程不允许施加过大的正弦波激励信号；其次，对于慢时变过程系统而言，试验所经历的时间较长，可能受到的干扰能量更大.因而，控制实践中，工程技术人员往往通过对象或系统的时域过渡过程来研究控制系统特性［3-9］.然而，通过这种时域分析手段难以掌握对象的本质特性.实质上，在充分激励的对象过渡过程数据中包含了多种频率谱信号［10-13］，如果能将这些信号的频率特性提取出并与对象输入信号进行比较，便可直接获取对象的频率特性，可为控制系统的设计和参数整定提供一种较为有效的方法.

笔者在充分分析阶跃信号频谱特性的基础上，提出了阶跃激励信号是一种理想的频率信号源的概念，并利用相关的频谱提取算法获取对象频率特性.仿真试验和实际应用结果表明：该方法能较为准确地计算出对象或系统的频率特性，并具有较强的抗干扰能力.

1 理想频率信号源

阶跃激励信号是控制工程领域中时常采用的激励信号之一，通过阶跃响应可以判断控制回路的各种品质特征，通过阶跃响应也可以辨识出对象的近似参数模型.阶跃响应分析往往被人为地局限于时域分析中，仅仅用于完成控制回路表象上的分析，其深层次的频率特性分析被遗忘或者因缺乏有效手段获取对控制系统有益的信息而放弃.本质上而言，阶跃响应的背后蕴藏着系统的频率特性［10-13］，可以通过分析阶跃信号本身的频率特性说明这点.

对于非周期的阶跃信号，可以进行傅里叶变换为各种频率下周期信号的叠加，单位阶跃变换后的结果如下［10-13］：

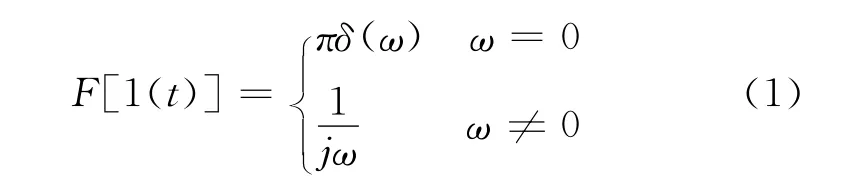
式中：δ（ω）为单位冲激函数；j为虚数单位；ω为角频率，rad／s.

从式（1）可以看出，阶跃信号具有以下几点显著特征：

（1）阶跃信号包含了全频谱的信号.

（2）当ω＞0时，幅值同频率成反比，相位恒等于π／2.

（3）对于0＜ω＜1，低频段的幅值较大，该频段下相应的信噪比也就较大.

换言之，阶跃信号是由无数个连续频率、初始相位为-90°的余弦或0°正弦波信号叠加而成的，且这些信号在低频段（大多数工业过程均在低频段）的幅值较大.由此可知，由于阶跃信号包含了连续频谱成分，本质上已具备了频率响应试验的信号特点.因而，系统或对象的阶跃响应实际上是由无数的连续频谱正弦波信号共同激励产生的.如果将对象或系统看作线性系统，那么阶跃响应结果也含有各种频率下激励的效果.特别是对于慢时变工业过程而言，由于低频成分具有较大的幅值，一般系统或对象也将得到充分激励.基于以上特点，笔者提出了阶跃激励信号实际上是一种理想频率响应信号源的观点.如何识别出阶跃响应过程信号中各种频率信号的幅值和相位是进行对象或系统频域分析的关键.笔者采用了一种新型的数字滤波器，能快速有效地分辨出系统或对象的频率特性.

2 点频滤波器

2.1 点频滤波器基本概念

上文已明确指出，阶跃激励信号本质上是理想的频率响应信号源.阶跃响应能够成为频域分析的原始数据需要解决的关键问题是将阶跃响应数据的频谱特性分布分离和识别出来.带通滤波器可以实现将需要的频率段信号从阶跃响应中提取出来，而其他频率信号均将被滤除.理想情况下，如果带通滤波器相应的带宽无穷小，那么就可以获得某个频率点上“单色”信号.为实现这个目标，首先分析典型的带通滤波器，见图1.

图1 LCR 带通滤波器Fig.1 LCR band-pass filter

图1中X（s）、Y（s）表示LCR 电路输入、输出信号的Laplace形式，可以用下面的传递函数表述两者之间的关系：

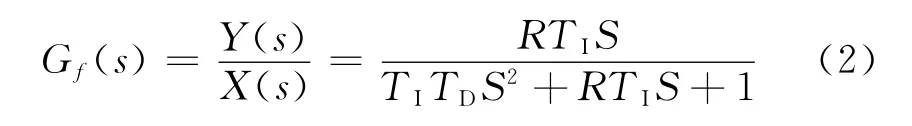
式中：R为电阻，Ω；TI为积分常数，s；TD为微积分常数，s；S为复数频率单位，在频率域令S＝j·ω.

其中，LCR 带通滤波器的中心频率为：

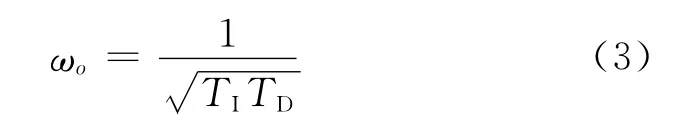
所谓带宽，即为信号通过滤波器后，带通滤波器输出的信号幅值衰减到中心频率0.707倍时对应的频率宽度，用ΔB-3dB表示.

LCR 带通滤波器响应的品质因数定义如下：

当品质因数远远大于1时，有以下近似关系式：

联立式（4）和式（5）可得：

由式（6）可知：当R无穷小时，LCR 滤波器带宽将变得无穷小，对应的品质因数无穷大.

为进一步阐述该形式滤波器的特性，需考察滤波器的增益.通过式（2）可得滤波器的增益为：

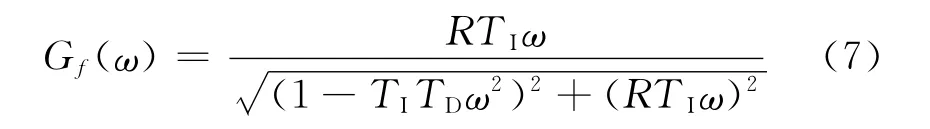
当信号频率ω等于LCR 带通滤波器中心频率ωo时，即（1-TITDω2o）2＝0，则：

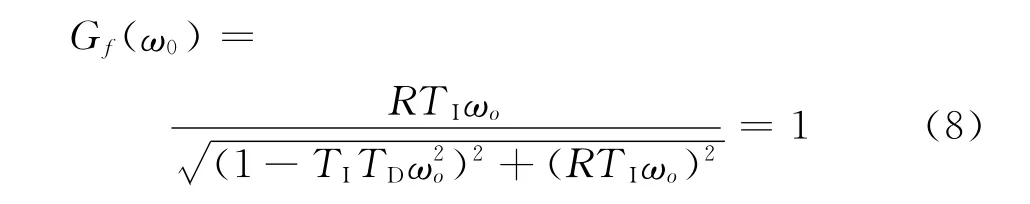
当信号频率ω不等于LCR 带通滤波器的中心频率ωo时，即（1-TITDω2）2≠0，且R趋于无穷小，则有：

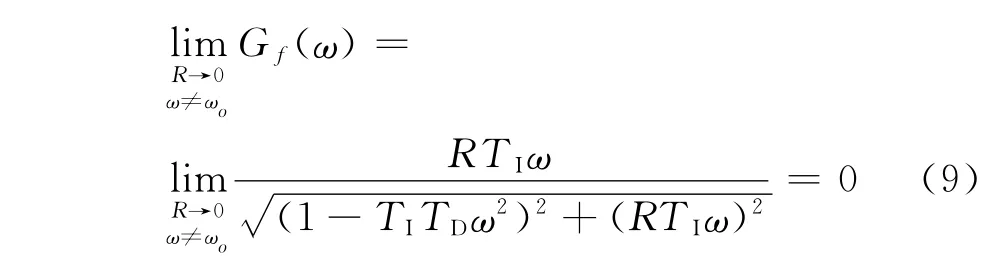
根据式（8）和式（9），得到了带宽无穷小的LCR带通滤波器，可以用图2表示其滤波效果.信号通过该滤波器后，只有频率ω＝ωo的信号才能通过滤波器，且其幅值不衰减；其他频率信号幅值均衰减为0.由于该滤波器仅能通过与滤波器中心频率相等的频率信号，我们称该滤波器为“点频滤波器”.有了这种滤波器后，便可以提取阶跃信号或阶跃响应中各种频率的成分特性.

图2 点频滤波器特性图Fig.2 Characteristics of single-frequency-pass filter

2.2 点频滤波器内在机理分析

用带宽无穷小的LCR 带通滤波器就得到了“点频滤波器”.LCR 带通滤波器本质上为无源LCR 振荡回路，带宽无穷小的LCR 带通滤波器，也就是无源LCR 振荡回路的R无穷小，相当于无源LCR 振荡回路中能量衰减也无穷小.因此，在经过输入阶跃信号或阶跃响应信号的激励后，得到输出振荡幅值永不衰减的频率信号，这也是点频滤波器最主要的特性之一.

2.3 实际点频滤波器

实际应用中的点频滤波器R值不可能趋于无穷小，而且也无法构建带宽为无穷小的滤波器，只能给出一个带宽足够小的LCR 带通滤波器，这种近似的点频滤波器被称作实际点频滤波器.点频滤波器与实际点频滤波器的主要区别在于：前者输出频率信号的幅值永不衰减，后者输出频率信号幅值会随时间逐渐衰减，幅值时间衰减率与LCR 带通滤波器带宽之间呈正相关性，带宽越小、幅值时间衰减率也越小.当幅值随时间的衰减率小到一定程度时就足够满足实际频率信号提取的需求.

2.4 频率特性不变性理论证明

为了论述本文提出的方法可用，进行以下论证.

采用实际点频滤波器后，对于分析阶跃信号激励下线性对象或系统的频率特性同实际一致即可证明频率特性不变.系统或对象的频率分析图类似于图3.假设待分析对象的传递函数是Go（s），实际点频滤波器的传递函数是Gf（s），对象输入信号是U（s），对象输出信号为Y（s），则：

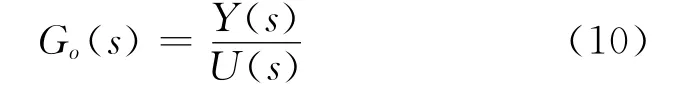
经过实际点频滤波器之后，输入信号和输出信号分别如下：

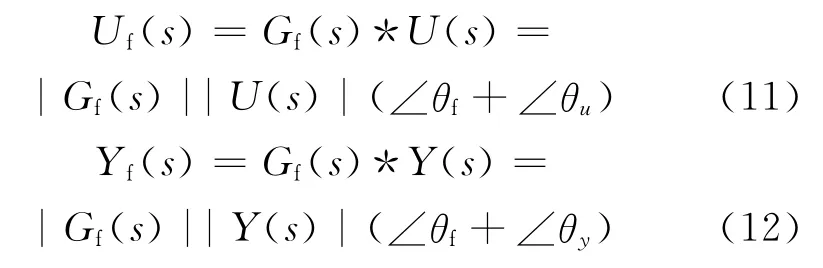
式中：下标f表示实际点频滤波器相关的量；∠θf为实际点频滤波器的传递相角值；∠θu为对象输入信号的相角值；∠θy为对象输出信号的相角值.

对于任何中心频率滤波后的信号分别进行相位、幅值比较之后，即两滤波信号幅值的比值和相位的差值组合成了一个对象G（s）的频域特性，即

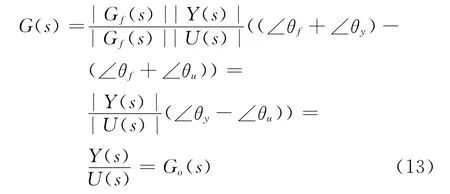
由式（13）可知：经过幅值和相位比较的频率特性同实际过程对象的频率特性一致，与滤波器的带宽和中心频率没有直接的联系.因而，证明采用实际点频滤波器后，对象或系统的频率特性不变.

3 点频率滤波器方法与傅里叶变化算法对比

点频滤波器方法相对于传统的傅里叶变化算法来说，算法编程极为简单.

傅里叶变化算法是将时间域信号转换为频率域信号的有效工具，可用于阶跃信号或阶跃响应信号中连续频率谱成分的分析计算.但从另一个角度看，既然阶跃信号或阶跃响应信号内包含了连续频率谱成分，自然也可以用最简单的点频滤波器方法直接获取频率谱成分.

点频滤波器方法与傅里叶频谱分析方法的本质区别在于：前者直接获取频率谱成分，工程应用方便；后者通过无穷多种频率信号拟合法计算出频率谱成分，计算复杂.

4 仿真试验

为验证文中所提出理想频率信号源和点频滤波器的有效性，进行了以下仿真试验.试验中将实际点频滤波器的带宽设为10-6rad／s，仿真对象是一个等容二阶系统，其时间常数为50s.仿真试验过程方框图见图3.图3中点频滤波器1输出端得到对象输入端的频率信号，在点频滤波器2输出端得到对象输出端的频率信号.实际点频滤波器的中心频率和带宽调节、频率特性的频率范围等内容放在实际应用章节介绍.

首先，笔者进行了阶跃信号经过实际点频滤波器的仿真试验，得到了如图4所示的初始频域幅值特性图，给出的频率范围是0.000 5～0.01rad／s.

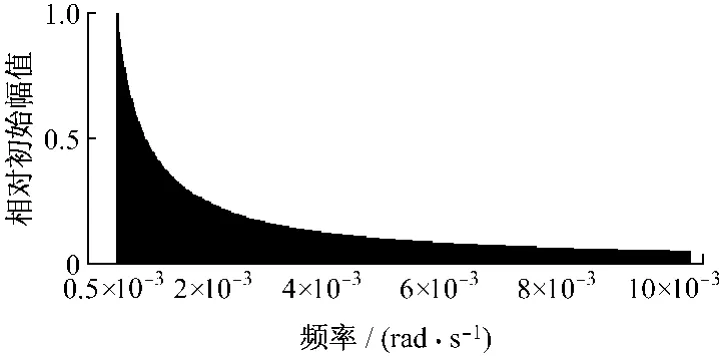
图4 初始幅值与频率关系图Fig.4 Relationship between initial amplitude and frequency of step signal after passing though the single-frequency-pass filter

频率为0.000 5rad／s的信号，其幅值随时间的衰减关系见图5.从图5可看出：输出幅值衰减到初始幅值0.707倍的时间大约需要1 950h，已足够满足实际幅值和相位提取的需求.

试验期间，在阶跃信号上加入多种频率的干扰信号时，得到实际点频滤波器在频率0.01～0.30 rad／s的初始频域幅值特性，见图6.

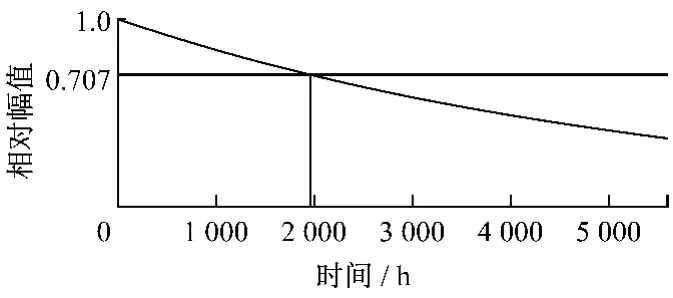
图5 信号的幅值随时间衰减关系图Fig.5 Curve of signal amplitude damping with time

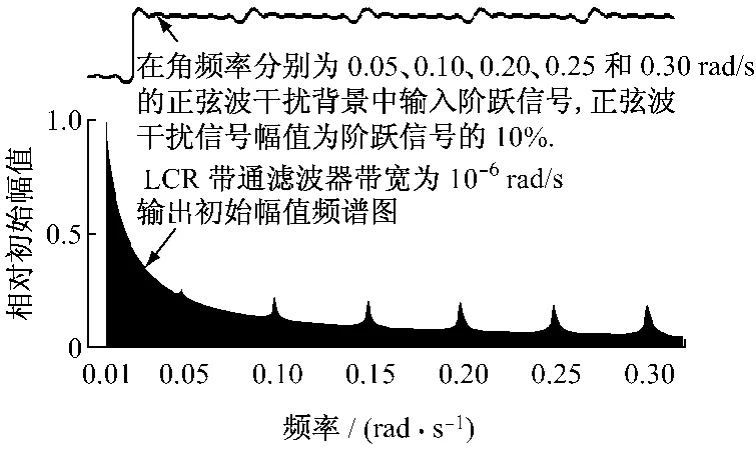
图6 输出信号幅频特性图Fig.6 Amplitude-frequency characteristics of step signal with noise after passing through the single-frequency-pass filter

由图6可知：通过滤波器之后，干扰信号的频率能够很容易被识别出来，为进一步消除干扰提供了帮助.仿真过程中，在施加阶跃信号的同时，在输出通道上加入了多种频率的干扰信号，并分别将可变中心频率的实际点频滤波器分别接入在对象的输入和输出端，滤波之后的信号进入相位、幅值比较器，从而获得对象或系统的频率特性.首先，抽取了中心频率为0.02rad／s的仿真结果图（图7）.图7中两条正弦波曲线分别是两个实际点频滤波器的输出信号.对比两个信号可知：对象输出端频率信号幅值比对象输入端频率信号的幅值下降了0.5倍，相位滞后了90°.该结果完全符合对象传递函数在0.02 rad／s处对应的频率特性.仿真结果证明了笔者提出方法的正确性和有效性.

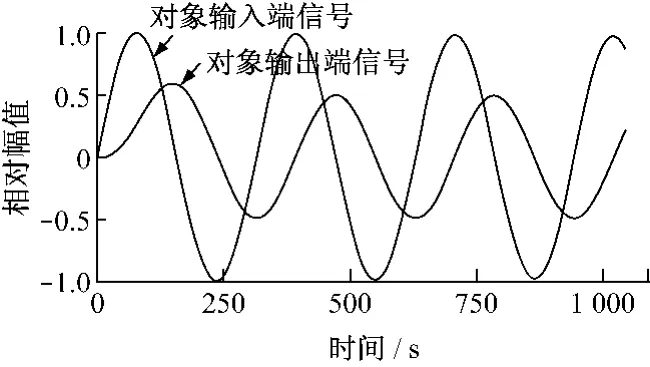
图7 频率为0.02rad／s的对象输入信号和输出信号比较图Fig.7 Comparison of relative amplitude between input and output signal at f＝0.02rad／s

为了进一步证明笔者提出方法的有效性，给出了频率为0.001～0.230rad／s的频率特性仿真结果，见图8和图9.

图8 幅频特性仿真试验结果图Fig.8 Amplitude-frequency characteristics obtained by simulation test

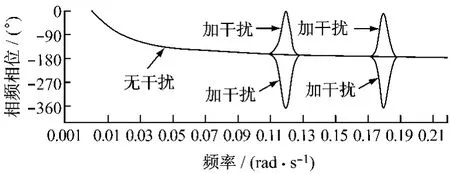
图9 相频特性仿真试验结果图Fig.9 Phase-frequency characteristics obtained by simulation test

从图8和图9可以看出：仿真结果和对象理论上的频率特性在试验频段上重合，仅仅在加入干扰的两个频率点（0.12rad／s和0.18rad／s）存在差异，干扰信号在频率特性的分析下暴露无遗.因此，在实际的频率分析中可以将相位和幅值同时有突变的频率点剔除，提高整个系统的抗干扰能力.

5 实际应用

笔者将所提出的方法运用于广东沙角发电C厂2号660 MW 机组过热汽温控制系统频率特性的离线辨识［14］，该系统的阶跃响应趋势见图10.

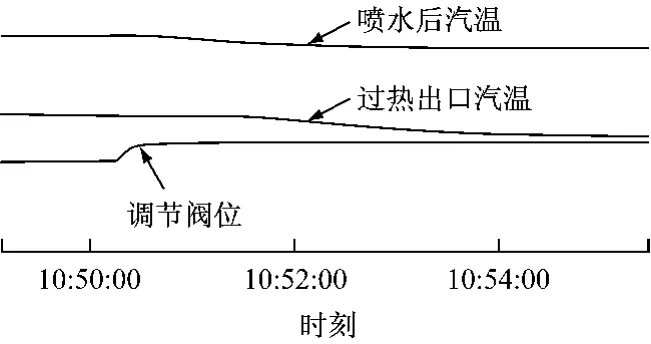
图10 过热汽温控制系统在500 MW 负荷阶跃响应趋势图Fig.10 Step response of superheated steam temperature control system at 500 MW

5.1 离线辨识数据处理

将图10中的调节阀位、喷水后汽温和过热器出口温度离线数据分别进行时间延拓处理，目的是将离线数据截止后的时间尺度延拓到足够长，以满足离线计算的需要.具体为：离线数据终止后的部分分别用各自离线数据的最终值进行填充，然后同步将各时间延拓数据按前后次序逐点输出，以供离线程序计算.该离线数据的时间间隔为1s.

实际的辨识用了3个实际点频滤波器，实际点频滤波器的带宽设为10-6rad／s.

5.2 实际点频滤波器的中心频率和带宽调节

根据式（3）和式（6），考虑到计算方便，令TI＝TD＝To，则得到LCR 带通滤波器中心频率调节公式和LCR 带通滤波器带宽调节公式：

将TI＝TD＝To代入式（2），并进行适当的变形，得到了闭环回路的具体形式，见式（16），它实现了带通滤波器的功能.

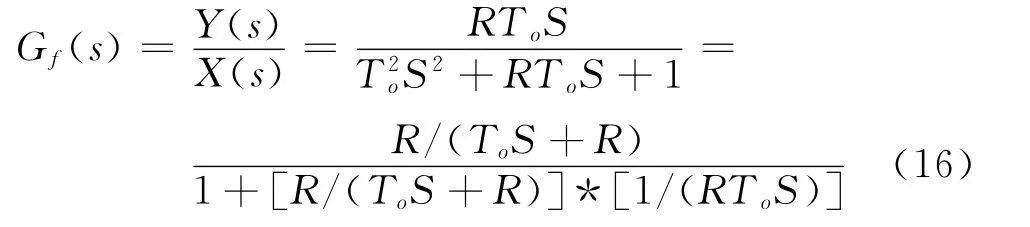
由式（14）、式（15）和式（16）对应的实际点频滤波器系统见图11.

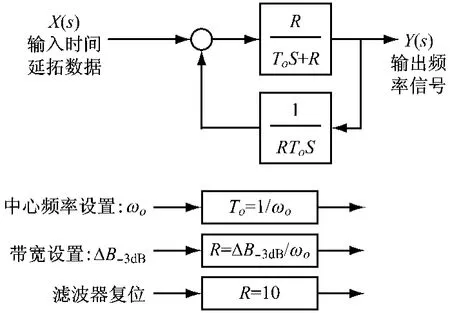
图11 实际点频滤波器系统图Fig.11 Block diagram of a practical single-frequency-pass filter

如图11所示，得到了设定中心频率和带宽的实际点频滤波器.其中滤波器复位端用于复位控制，其原理是：进行复位控制时，将滤波器的R设置为一个较大值，使输出频率信号的幅值迅速衰减为零.

具体的频率信号离线辨识过程是：将时间延拓数据接入实际点频滤波器输入端，设置滤波器中心频率和滤波器带宽，在每次开始频率信号辨识前首先对滤波器进行复位控制.

3个实际点频滤波器频率信号辨识是同步进行的，分别得到调节阀位频率信号、喷水后汽温频率信号、过热器出口温度频率信号.

5.3 确定频率特性的频率范围

理论上，阶跃频谱信号或阶跃响应频谱信号提供了海量的信息量，频率特性的频率范围是无限制的.实际上仅是最高可辨识频率受离线数据的时间间隔限制，实际离线数据2点之间的时间间隔为1 s，按照信号采样频率最少为信号频率2倍计算，则可辨识的最高频率为0.5 Hz，对应角频率为3.14 rad／s.也就是说，辨识频率范围上限为3.14rad／s，但其下限没有限制.

对于2个辨识频率信号的比较，可以从上限频率开始，设定连续辨识频率间隔（如0.001rad／s），不断减少辨识频率值和不断得到频率特性辨识结果，当2个辨识频率信号比较得到的幅频增益基本稳定后，停止辨识，此时的辨识频率即为下限辨识频率.如此则得到了设定连续辨识频率间隔的频率特性和辨识频率上限到下限范围的频率特性.

5.4 实际频率特性辨识

图12为过热器出口温度频率信号与阀位指令频率信号相比较得到的幅值频率特性图，频率范围0.001～0.060rad／s，辨识频率间隔为0.000 1rad／s.

图12 过热器出口温度相对阀位幅值频率特性Fig.12 Amplitude-frequency characteristics of superheater outlet temperature relative to valve level

图13为喷水后汽温频率信号与阀位指令频率信号相比较得到的幅值频率特性图，频率范围0.001 ～0.060rad／s，辨识频率间隔为0.000 1rad／s.

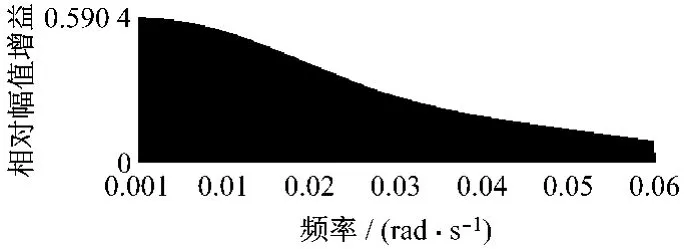
图13 喷水后汽温相对阀位幅值频率特性Fig.13 Amplitude-frequency characteristics of sprayed steam temperature relative to valve level

5.5 过热器对象模型频率特性辨识

过热器出口温度频率信号与喷水后汽温频率信号相比较得到过热器对象模型频率特性，见表1和图14、图15.

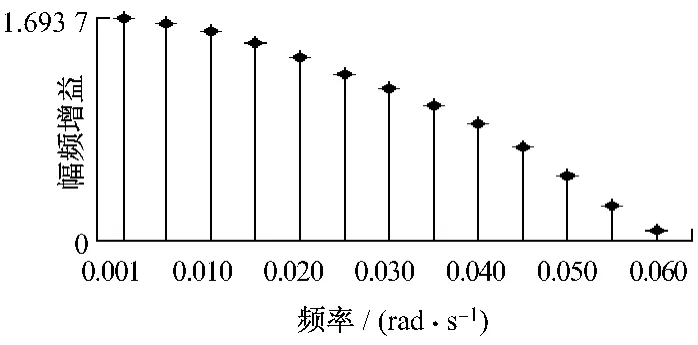
图14 过热器对象模型幅值频率特性辨识图Fig.14 Identification graph of amplitude-frequency characteristics with superheater object model

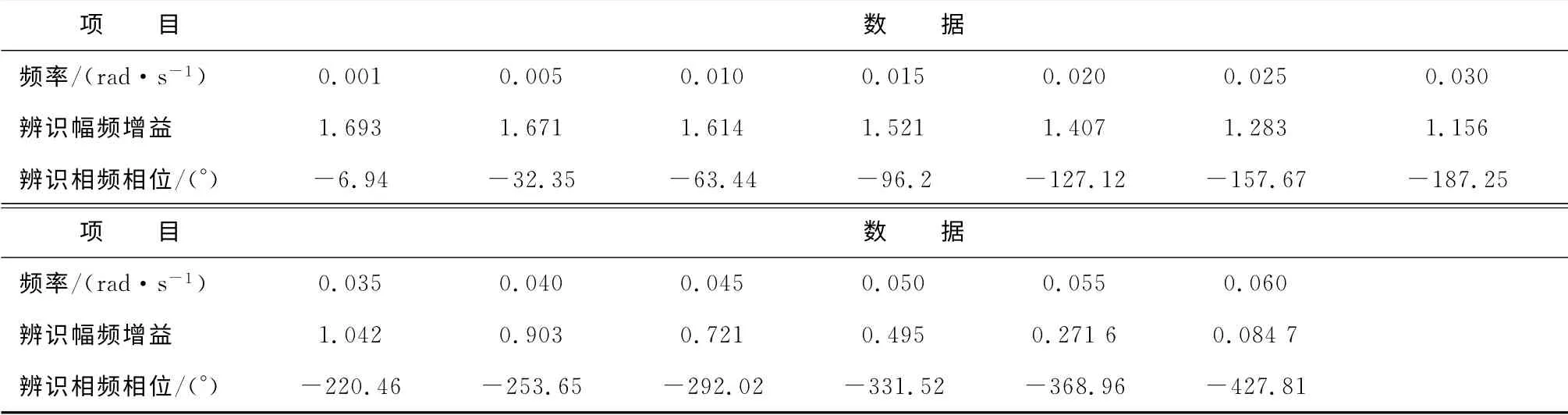
表1 过热汽温对象模型频率特性辨识结果表Tab.1 Identification results of frequency characteristics with superheated temperature object model

图15 过热器对象模型相位频率特性辨识图Fig.15 Identification graph of phase-frequency characteristics with superheater object model

由图14和图15可见：过热器对象的频率特性幅频增益和相频相位曲线是单调下降的，基本符合高阶对象的频率特性.根据所辨识出的频率特性，还可继续辨识出该对象的近似数学模型，但限于篇幅，这个问题在本文不再继续讨论.

6 结 语

在分析阶跃信号频率特性的基础上，提出了阶跃信号是对象频域分析的理想激励信号源.在带通滤波器的基础上提出了点频滤波器的具体形式，并通过了仿真试验和实际应用证明了该方法的有效性和正确性.

所提出的方法将在频域范围的控制系统性能分析、参数模型辨识和干扰信号的分析等方面有实际应用价值.

［1］THAM M T.Why frequency response［R］.Australia：University of Newcastle，1999：1-17.

［2］WANG Y G，CAI W J，GE M.Decentralized relaybased multivariable process identification in the frequency domain［J］.IEEE Trans on Automatic Control，2003，48（5）：873-877.

［3］田沛，宿喜峰，马平，等.基于自抗扰技术的主汽温全程控制［J］.中国电机工程学报，2006，26（15）：73-77. TIAN Pei，SU Xifeng，MA Ping，etal.Full scope control on the main steam temperature based on ADRC technology［J］.Proceedings of the CSEE，2006，26（15）：73-77.

［4］朱红霞，沈炯，李益国.一种新的动态聚类算法及其在热工过程模糊建模中的应用［J］.中国电机工程学报，2005，25（7）：34-40. ZHU Hongxia，SHEN Jiong，LI Yiguo.A novel dynamic clustering algorithm and its application in fuzzy modeling for thermal processes［J］.Proceedings of the CSEE，2005，25（7）：34-40.

［5］李萌，沈炯.基于自适应遗传算法的过热器温PID 参数优化控制仿真研究［J］.中国电机工程学报，2002，22（8）：145-149. LI Meng，SHEN Jiong.Simulating study of adaptive GA-based PID parameter optimization for the control of superheated steam temperature［J］.Proceedings of the CSEE，2002，22（8）：145-149.

［6］刘志远，吕剑虹，陈来九.基于神经网络在线学习的过热汽温自适应控制系统［J］.中国电机工程学报，2004，24（4）：179-183. LIU Zhiyuan，LÜ Jianhong，CHEN Laijiu.Superheated steam temperature adaptive control system based on neural network online learning［J］.Proceedings of the CSEE，2004，24（4）：179-183.

［7］安德玺，梁彦，周东华.一种基于滤波参数在线辨识的鲁棒自适应滤波器［J］.自动化学报，2004，30（4）：560-566. AN Dexi，LIANG Yan，ZHOU Donghua.A robust adaptive filter based on online filter parameter identification［J］.Acta Automatica Sinica，2004，30（4）：560-566.

［8］刘建民，韩璞，开平安，等.一种改进的α-β-γ滤波器和PID 控制器［J］.动力工程，2007，27（4）：551-554. LIU Jianmin，HAN Pu，KAI Pingan，etal.An improvedα-β-γfilter and PID controller［J］.Journal of Power Engineering，2007，27（4）：551-554.

［9］房方，刘吉臻，谭文.火电单元机组协调控制系统的多变量IMC-PID设计［J］.动力工程，2004，24（3）：360-365. FANG Fang，LIU Jizhen，TAN Wen.Multivariable IMC-PID design in the coordinated control system for fossil unit power plants［J］.Journal of Power Engineering，2004，24（3）：360-365.

［10］WANG Q G，ZHANG Y.Robust identification of continuous systems with dead-time from step responses［J］.Automatica，2001，37（3）：377-390.

［11］周建华.信号与系统［M］.北京：清华大学出版社，2009：219-220.

［12］RAUSCHER Christoph.Fundamentals of spectrum analysis［M］. München，Germany： Rohnde ＆Schwarz，2001：10-33.

［13］罗传翼，程桂芬，付家才.控制工程与信号处理［M］.北京：化学工业出版社，2004.

［14］丁峰，陈通文，萧德云.一般双率随机系统状态空间模型及其辨识［J］.自动化学报，2004，30（5）：652-663. DING Feng，CHEN Tongwen，XIAO Deyun.Statespace modeling and identification of general dual-rate stochastic systems［J］.Acta Automatica Sinica，2004，30（5）：652-663.