倾斜射流对移动平板表面紊动和传热特性的影响

叶纯杰，范俊生，潘红良

（华东理工大学 机械与动力工程学院，上海200237）

湍流射流冲击表面时会在冲击点附近产生较高的局部传热系数现象，被应用于诸多工业场合.随着工业自动化的发展和对产品加工效率要求的提高，需在较为封闭的环境下对产品进行自动化加工和连续作业，如带钢紊流酸洗以及乳化液漂洗，热轧后带钢表面的快速降温以及燃气透平叶片的冷却等都是在封闭条件下对运动的受热面进行传热或传质.

目前国内外对半封闭冲击射流下移动平板表面传热特性的研究较少，对倾斜射流下的移动平板传热和传质特性尚未有研究.李少华等［1］采用数值模拟的方法对复合角度斜射流下不同排孔结构对气膜冷却效率的影响进行了研究，结果表明复合角度射流可以使静止冲击面受热更为均匀；Sharif等［2］用RNGk-ε模型模拟了半封闭垂直入射流在不同雷诺数、射流高度和板速条件下平板表面传热系数和切应力系数的分布；Senter等［3］对垂直入射至移动平板的射流在不同入口雷诺数和不同平板速度与射流出口速度比下的湍动特性做了对比和分析，研究得出当平板运动速度大于射流出口速度时，对平板表面的湍动能分布影响较大；Chattopadhyay 等［4］采用大涡模拟湍流模型（LES）对三维半封闭垂直射流的流态和传热特性进行了数值计算，由于其所采用的计算区域较小，因此得出的结论不具有普遍意义.

笔者采用雷诺应力湍流模型（RSM）对二维半封闭狭缝斜射流冲击移动平板下的流场进行了计算，研究了入射角度、平板移动速度和运动方向对平板近壁湍动能和板面局部努塞尔数分布的影响，对工业上相似工况下的传热传质具有一定参考价值.

1 物理模型和湍流方程

二维半封闭射流模型如图1所示，射流经槽内顶部正中间的狭缝喷嘴以一定角度入射至平板表面，顶面为绝热固壁条件，底面为移动平板，左右侧为射流出口.入射喷嘴宽度D为10mm，计算区域长度L＝100D.Gori等［5］研究了半封闭空间内射流入射高度对静止平板表面传热系数的影响，得到最佳射流高度与射流入口直径之比为8︰1，因此按最佳入射高度确定入射高度H为80mm.设定入口雷诺数Re为10 960，其他变量为平板移动速度与入口流速比R（平板向右移动为正方向）和入射角θ（入口射流中心线与x轴夹角）.

图2为二维模型的网格分布示意图.分别对160×40、180×50、200×60、220×70、240×80和260×90的正四边形结构网格进行网格数目影响计算结果的模拟.计算表明：当网格分布达到260×90时，平板运动方向上的局部努塞尔数分布基本上不再发生变化，因而对以下的模拟均采用260×90的网格.

图1 二维半封闭射流模型图Fig.1 Two-dimensional geometry of moving plate impinged by confined slot-jet

综上所述，文中计算采用的喷嘴宽度D＝10 mm，计算区域长度L＝1 000mm，入射高度H＝80 mm，入口雷诺数Re＝10 960，网格分布为260×90，平板移动速度与入口流速比R和入射角度θ为变量.

Navier-Stokes方程能精确描述射流的流动和传热问题［6］.系统控制方程如下：

连续方程

动量方程

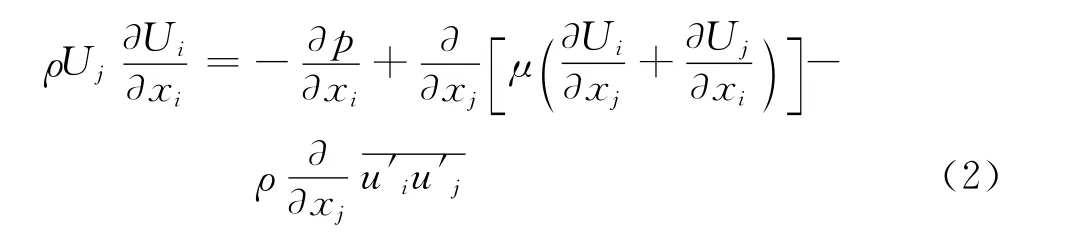
能量方程

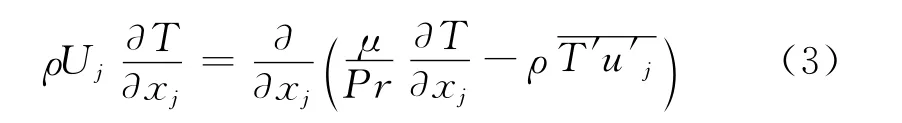
式中：U，p和T分别为平均速度，压力和温度；u′和T′分别为脉动速度和脉动温度；ρ，μ和Pr分别为平均流体密度、分子动力黏性系数和普朗特数.本文中采用加热空气作为射流介质，其密度和黏度分别为1.225kg／m3和1.789 4×10-5kg／m·s.

Craft等［7］比较了k-ε模型和雷诺应力方程对射流的模拟，发现雷诺应力方程对壁面压力应变项的模拟精度更高.所以笔者选用雷诺应力模型（RSM）来封闭流体的质量方程、动量方程和能量方程.RSM 在计算突扩流动分离区和计算湍流运输各向异性较强的流动时优于k-ε和RNGk-ε模型且计算量小于大涡模拟（LES），是一种非常有潜力的湍流模型.

2 边界条件和数值求解方法

将图2所示的整个流场作为计算区域，采用有限体积法离散控制方程.其中，对流项采用延迟修正的Quick格式离散，其具有三阶精度的截差，可产生比二阶迎风格式等更精确的计算结果；扩散项采用二阶截差的中心差分格式；压力-速度耦合采用Simplic算法.求解方程组需给定如下边界条件：

采用均匀的入口射速

式中：uin和vin分别为进口处射流在x和y方向的速度分量；kin和εin分别为进口处的湍动能和湍动能耗散项；Tin为射流温度；Uin为射流在入口的速度值.

出口选用局部单向化条件，即

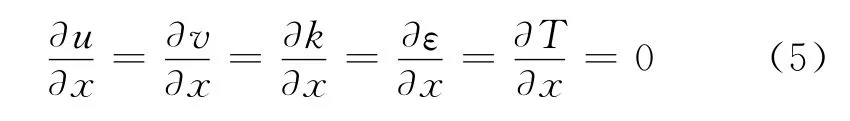
顶部封闭板采用无滑移条件，即

对于底部移动平板，壁面内计算采用壁面函数法，壁面条件为：up＝Up，vp＝0.不考虑封闭板与外界的自然对流及辐射换热，将封闭板面取为绝热壁面，即∂T／∂y｜y＝0＝0.平板面采用了等壁温条件，取平板温度Tp＝300K.其中，uc和vc分别表示射流在封闭板处x和y方向的速度分量；up和vp则表示平板在x和y方向的速度分量；Up表示平板移动的速度值.

3 RSM 模型试验验证

由于平板移动的斜射流方式缺少试验数据，因此无法直接比较数值模拟与试验数据间的吻合程度.但在半封闭垂直射流对移动平板流场分布的研究方面，Senter等［3］对入口雷诺数Re＝10 600，入射高度入射宽度比H／D＝8︰1，平板移动速度（板速）和入口流速比R为0和0.5条件下的射流口轴心线速度和湍流强度分布做了试验分析，数据可靠.采用RSM 湍流模型对其进行数值计算，得到无量纲化的射流轴心线速度（轴心线速度w与射流入口速度Uin之比）和湍流强度分布，与试验值进行对比，分别见图3和4.定义湍流强度为：

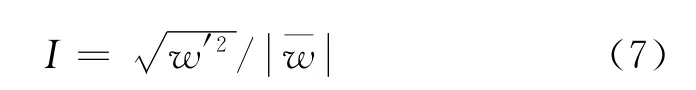
式中：w′和分别为射流轴心线上的湍流脉动速度与平均速度.

从图3和图4中可以看出，RSM 模型对射流中心线的速度分布和移动平板表面射流湍流强度分布也有很好的吻合性.因此，RSM 模型能够很好地模拟射流冲击移动平板下的流动和传热.

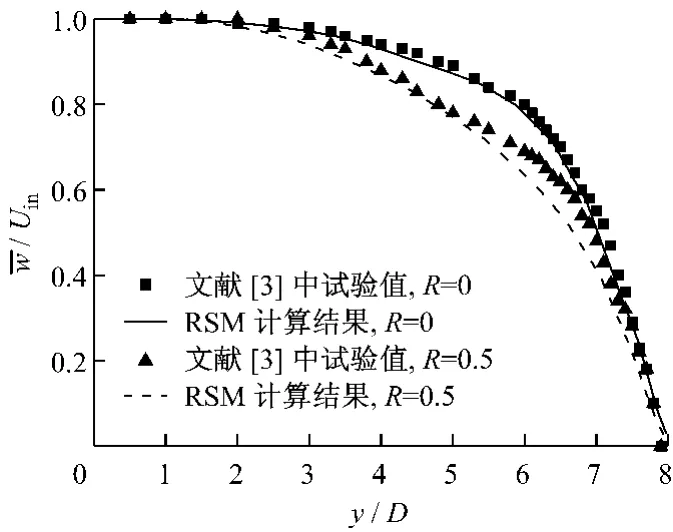
图3 射流口轴心线速度分布模拟值和试验值对比Fig.3 Comparison of velocity distribution along the jet centerline between simulated and experimental data

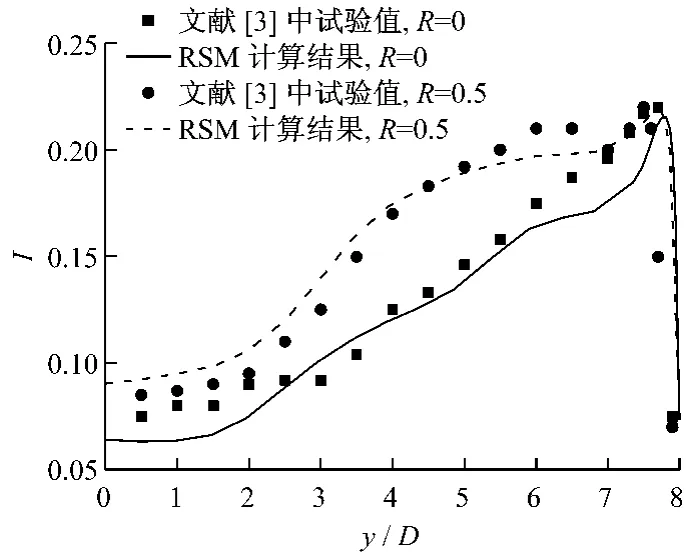
图4 射流口轴心线湍流强度分布的模拟值和试验值对比Fig.4 Comparison of turbulence intensity along the jet centerline between simulated and experimental data

4 模拟结果及讨论

由于上封闭板的作用，在低入射角下射流的卷吸作用使得射流在未到达底部移动平板就向一侧出口发展，因此将射入角大于70°的斜射流作为研究对象.Fitzgerald等［8］对半封闭平板射流的研究发现，入口雷诺数的变化对流场结构和近壁处湍流强度分布的影响较小，因此笔者只对入口雷诺数Re＝10 960时的射流流场进行分析.

4.1 射流角度和板速对近壁湍动能分布的影响

近壁湍动能作为表述平板近壁面速度脉动的参数，与壁面的传热和传质特性有着直接联系.将湍动能无量纲化处理得到k＊＝k／U2in.图5为不同入射角和板速下近壁面处（y／D＝7.98）湍动能k＊的分布.由于射流在平板冲击点附近产生的速度梯度最大，速度边界层最薄，因此在此处产生了湍动能峰值.在平板静止时（R＝0），此峰值随倾角的减小而减小.当平板向右移动时，倾斜射流在冲击点附近产生的湍动能随板速的增大先降低后大幅增高.这是因为低速时平板运动方向与射流方向相同降低了冲击点处的切应力，而随着平板速度的增大，平板运动产生的剪切应力大大提高了近壁处的湍动能.在x＞｜20D｜的冲击点以外区域，板速对湍动能强度起主要作用，｜R｜＝2时的近壁面湍流强度值约为平板静止时的30倍.板速较高时在左侧出口附近湍动能出现峰值，这是由于向右移动的平板在左侧出口近壁处形成回流，产生了较高的湍动能，向左移动的平板在右出口位置处也出现了相似的峰值.

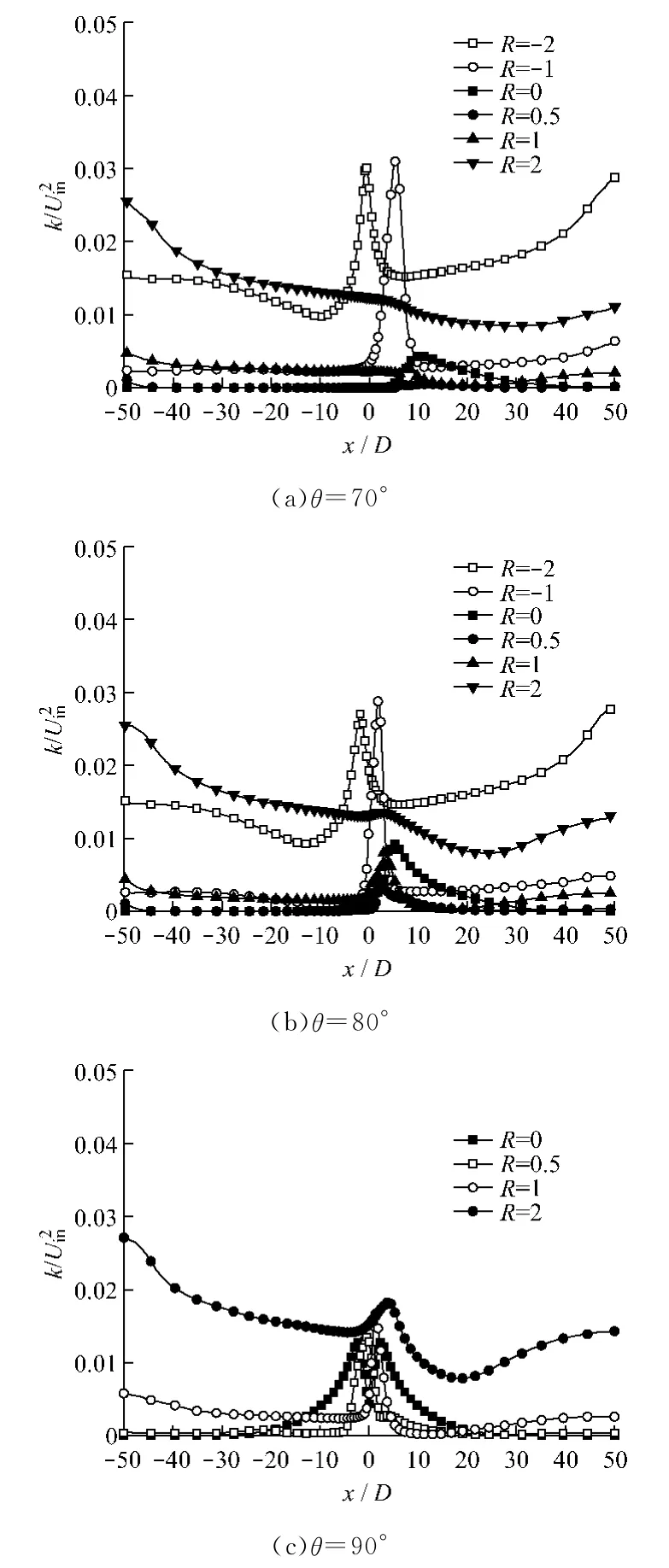
图5 不同板速和入射角下近壁面的湍动能分布Fig.5 Distribution of turbulent kinetic energy near the wall of moving plate at different plate velocities and jet angles

当平板向左运动与入射角方向相反时，倾斜射流在冲击点处的湍动能值较高.R＝-1时，入射角为70°和80°斜射流产生的湍动能k＊值最大，为0.03，大大高于垂直入射静止平板时在冲击点处的k＊值，此时在冲击点附近产生的湍动能要高于平板静止时的2 倍以上.对于R＝-2条件下的斜射流，从图5（a）和图5（b）可以看出：此时湍动能最大值的位置已偏向中心点左侧，说明高速向左运动的平板使得射流冲击点偏向流场左侧，因此R＝-2 时在冲击点的湍动能峰值较R＝-1时要小.

4.2 射流角度和板速对平板表面传热特性的影响

平板运动使得出口边界处产生回流，为了减小出口回流对传热特性的影响，x方向选取为-25D～25D.局部努塞尔数是表征传热系数增大倍数的无量纲参数，定义为：

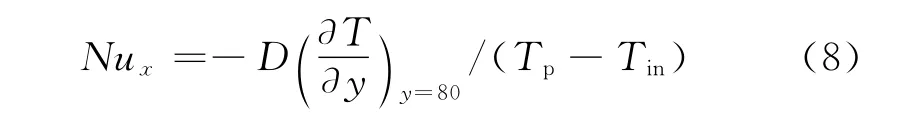
不同板速和入射角下平板表面局部努塞尔数分布见图6.平板静止时射流在冲击区域产生较高的温度梯度，表征温度梯度的局部努塞尔数值较高.平板运动引起射流的偏转导致冲击力下降，致使冲击区域的速度和温度边界层增厚.因此，当平板向右运动时，局部努塞尔数在冲击点处的峰值随板速提高而降低，峰值对应的位置点也向平板运动方向偏移，R＝2时的峰值下降为平板静止时的60%以下，而平板表面努塞尔数的整体分布随板速的提高趋于均匀.Chattopadhyay 等［4］对垂直入射移动平板的研究也得到了相同的结论.而对于冲击点以外区域，板速的提高大大提高了局部努塞尔数.当R＝-1时，斜射流下在冲击点处产生的局部努塞尔数峰值最高，约为R＝1时的3倍，且略高于垂直入射静止平板时的努塞尔数峰值.因此，对于连续作业的强化传热，采用一定板速与入口射速之比的斜射流能够获得较好的传热效果.

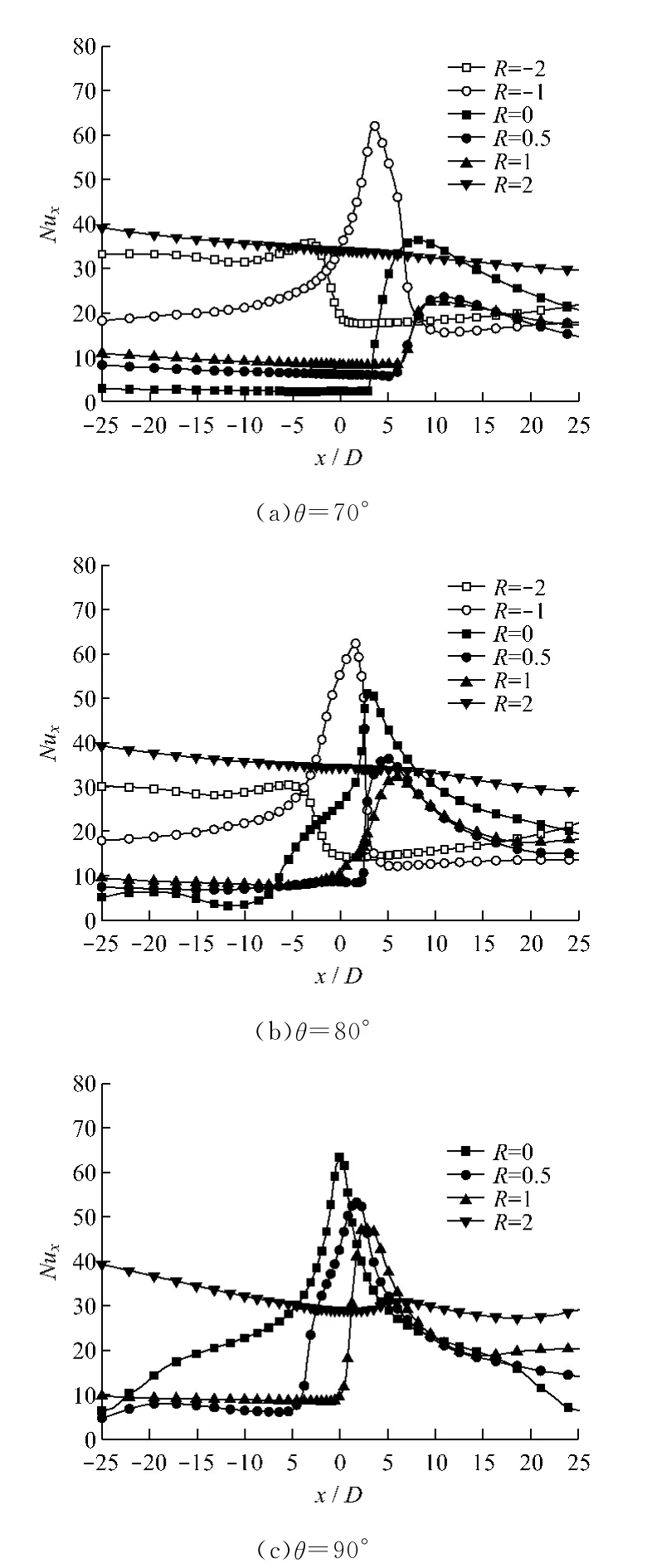
图6 不同板速和入射角下平板表面局部努塞尔数分布Fig.6 Distribution of local Nusselt number on the surface of moving plate at different plate velocities and jet angles

冲击点附近最大努塞尔数Numax随板速的变化见图7.倾斜射流下，当板速与入射角方向相同时，最大努塞尔数随板速的提高先降低后升高.在板速较低时，大入射角时产生的温度边界层较薄，最大努塞尔数值较大；而当板速提高到R＝2时，板速的影响大于入射角的作用，此时各入射角下的最大努塞尔数趋于同一值.与最大湍动能相同，当平板运动方向与入射角方向相反且入射角为80°时，射流在冲击点处能获得最大努塞尔数.

平板表面平均努塞尔数分布见图8.板速较低时，垂直入射下的平均努塞尔数要稍高于斜射流下的平均值；随着板速的提高，不同入射角下平均努塞尔数值的差距减小，此时板速使平板表面产生了较高的剪切流，大大提高了传热效率.Raju 等［9］对非封闭条件下射流对移动平板表面传热的研究得出：当平板移动速度小于射流入口速度时，板速对表面平均努塞尔数的分布影响不大；而板速大于入口射速时，平均努塞尔数大大提高.从图8可以看出：对于半封闭射流条件，当板速超过入口射速时，板速对平板表面传热的影响逐渐显著.而斜射流下R＝-1时也能一定程度上保持较高的平均努塞尔数，且受热面越大，平板移动产生的传热效果越显著.

图7 冲击点附近最大努塞尔数随板速的变化Fig.7 Variation of the maximum Nusselt number with plate velocity and jet angle

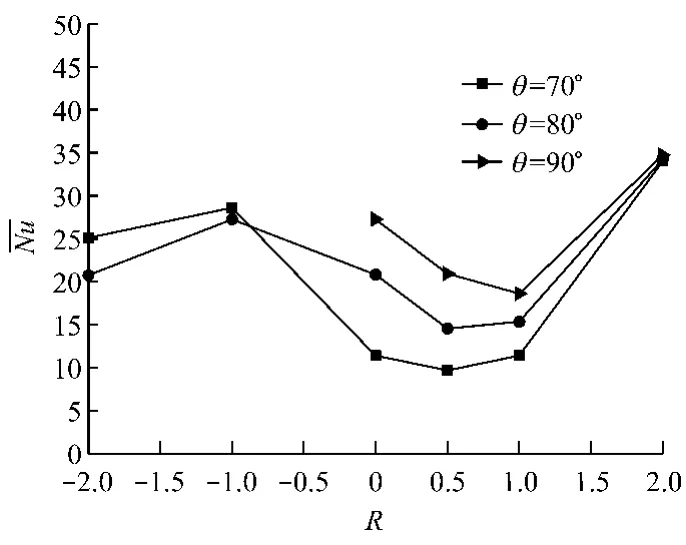
图8 平板表面平均努塞尔数分布Fig.8 Variation of the average Nusselt number with plate velocity and jet angle

5 结 论

（1）板速的提高增加了平板近壁处的湍动能，当板速为入口射速的2倍时，整个板面上的近壁湍动能大幅提高；当平板运动方向与入射角方向相反且R＝-1时在冲击点附近产生的湍动能最高，为静止时的2倍以上.

（2）当板速与入射角方向相同时，局部努塞尔数在冲击点处的峰值随板速升高而降低，而整体分布趋于均匀；冲击点以外区域，板速的提高大大提高了局部努塞尔数，当R＝-1且入射角为80°时，斜射流下在冲击点处产生的局部努塞尔数峰值最高.

（3）平板运动速度较低时，垂直入射下的板面平均努塞尔数要高于斜射流下的平均值；随着板速的提高，平均努塞尔数先降低后大幅升高，且不同入射角下平均努塞尔数的差距逐渐减小；此外，受热面越大，平板移动产生的传热效果越显著.

（4）当平板运动方向与倾斜射流方向相反且板速和射流速度大小相同时，能够在冲击点附近以及整个板面上都获得较好的紊动和传热效果.

［1］李少华，彭涛，张玉，等.复合角度对称射流气膜冷却效率的数值研究［J］.动力工程，2009，29（3）：236-240. LI Shaohua，PENG Tao，ZHANG Yu，etal.Numerical research on film-cooling efficiency of injection with opposite orientation compound angles［J］.Journal of Power Engineering，2009，29（3）：236-240.

［2］SHARIF M A R，BANERJEE A.Numerical analysis of heat transfer due to confined slot-jet impingement on a moving plate［J］.Applied Thermal Engineering，2009，29（2）：532-540.

［3］SENTER J，SOLLIEC C.Flow field analysis of a turbulent slot air jet impinging on a moving flat surface［J］.International Journal of Heat and Fluid Flow，2007，28（4）：708-719.

［4］CHATTOPADHYAY H，SAHA S K.Turbulent flow and heat transfer from a slot jet impinging on a moving plate［J］.International Journal of Heat and Fluid Flow，2003，24（5）：685-697.

［5］GORI F，BOSSI L.Optimal slot height in the jet cooling of a circular cylinder［J］.Applied Thermal Engineering，2003，23（7）：859-870.

［6］刘沛清.自由紊动射流理论［M］.北京：北京航空航天大学出版社，2008：32-33.

［7］CRAFT T J，GRAHAM L J W，LAUNDER B E.Impinging jet studies for turbulence model assessment：II.an examination of the performance of four turbulence models［J］.International Journal of Heat Mass Transfer，1993，36（10）：2685-2697.

［8］FITZGERALD J A，GARIMELLA S V.A study of the flow field of a confined and submerged impinging jet［J］.International Journal of Heat and Mass Transfer，1997，41（8）：1025-1034.

［9］RAJU K S，SCHLUNDER E.U.Heat transfer between an impinging jet and a continuously moving flat surface［J］.Heat and Mass Transfer，1977，10（2）：131-136.