一种评判煤灰结渣特性的新方法

文孝强， 刘彦臣， 关晓辉

（东北电力大学 教务处，吉林132012）

煤灰结渣是一种非常复杂的现象，美、英、西德和澳大利亚等国早在上世纪60年代初就对其形成机理进行了大量研究，但至今尚无定论［1］.近年来，国外研究人员总结出许多结渣经验判别指标，直接提供工程上应用，国内在这方面也有不少研究.归纳起来，主要包括以下几个方面：（1）根据煤灰物理特性对受热面结渣特性的预测，其中包括根据煤灰的熔点温度以及灰渣的黏度特性等进行预测.而前者又包括煤灰的变形温度、软化温度、熔点结渣指数等.西安热工研究院利用灰熔点结渣指数对我国24个电厂入炉煤质的灰熔点结渣指数与现行情况作了对照研究，发现灰熔点类型结渣指数分辨力为50%～60%.由于灰熔点结渣指数仅单纯考虑了煤灰本身的结渣倾向，从这个意义上说，灰熔点具有较高的分辨率.（2）根据煤灰成分特性对受热面结渣特性的预测，其中包括根据煤灰的单一成分以及煤灰成分的综合比值等进行预测.其中单一成分又包括根据铁含量、碱金属含量以及氯含量等进行预测.而煤灰成分的综合比值又包括利用煤灰的硅比、碱酸比、硅铝比、铁钙比等进行预测［2］.（3）结渣特性的综合预测，其中包括综合判别指数［3］、模糊数学［4－7］、人工神经网络［8－10］、模式识别［11－13］、最小二乘支持向量机等［14］.利用模糊数学对结渣进行评判有效地克服了单一指标分类界限过于明显的问题，而且与综合指数相比，它又很好地解决了权重过于平均化的问题，但是权值确定的正确与否直接关系到评判的最终结果，就目前来讲，权值主要靠实际判别的准确度来确定，所以此方法受实际统计结果的影响较大；利用人工神经网络对燃煤结渣特性进行评判时，训练样本较少时得到的权值不具代表性；模式识别方法在煤灰结渣预测和评判方面应用较少，但是如果能将用于辨识的模型的数据库建立起来，此种方法在预测煤灰结渣方面将是一种有意义探索.笔者基于偏最小二乘回归算法建立了煤灰结渣特性预测模型.

1 偏最小二乘回归算法

1.1 概述

偏最小二乘回归（PLS）是对一般最小二乘回归［15］（OLS）的扩展，是集多因变量对多自变量的回归建模以及主成分分析为一体的多元数据分析方法，在一次计算之后即可同时实现预测建模和多变量系统的综合简化.PLS不仅提供了一种多因变量对自变量的回归建模方法，而且有效解决了变量之间的多重相关性问题，适合在样本容量小于变量个数的情况下进行回归建模，可实现多种多元统计分析方法的综合应用.由于PLS回归建模有很多优点，因此目前在很多方面都有应用.

1.2 建模

设X经过标准化处理以后的数据矩阵为E0＝（E01，E02，…，E0p）n×p，Y 经过标准化处理以后的数据矩阵为F0＝（F01，F02，…，F0q）n×q.若t1、u1分别为E0、F0的第一个成分，t1＝E0w1，‖w1‖＝1，u1＝F0c1，‖c1‖＝1.要求t1、u1能分别很好地代表X与Y 中的信息，应该有var（t1）和var（u1）均取得最大值.另一方面，又要求t1对u1有最大的解释能力，即t1、u1的相关程度应达到最大值.因此，在偏最小二乘回归中体现为t1、u1的协方差达到最大.数学表述为求解下列优化问题：

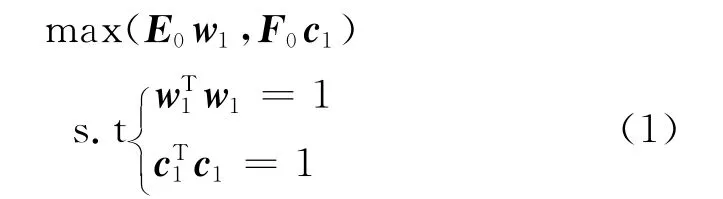
变换为拉格朗日算法形式为：

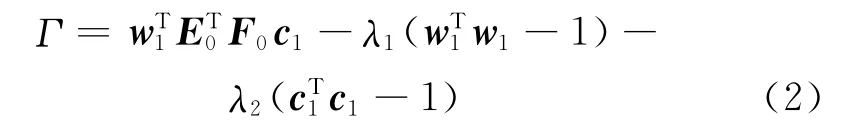
分别对Γ 求λ1，λ2，w1，c1的偏导数，并令其为0，则

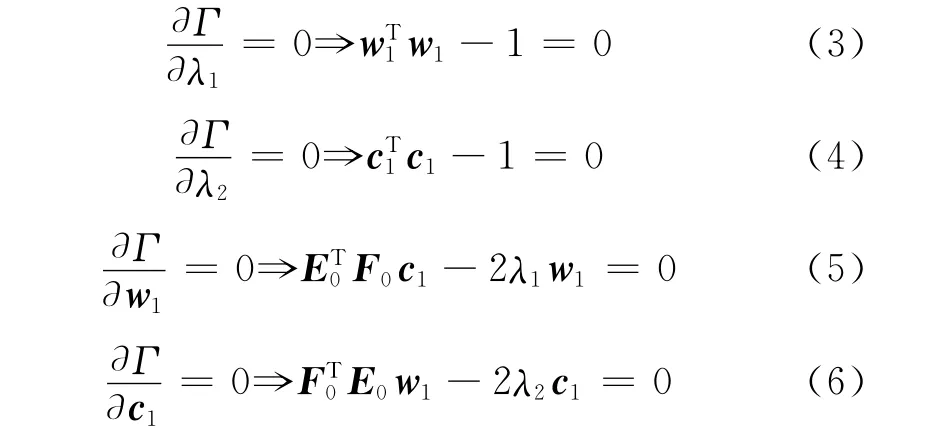
由式（3）～式（6）可推导出：

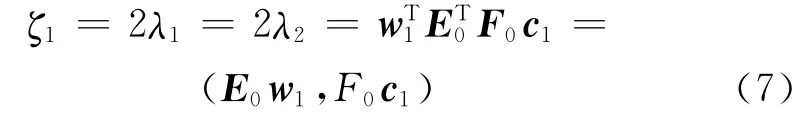
则ζ1便是优化问题的目标函数值.经求解得：

因此，w1、c1分别是矩阵的特征向量，对应的特征值皆为要求取最大值，所以，w1、c1是对应于矩阵最大特征值的单位特征向量.由w1、c1可得到成分t1＝E0w1，u1＝F0c1.于是，可得E0和F0对t1的回归方程

式中：p1和r1是回归系数向量分别是2个回归方程的残差矩阵.

用残差矩阵E1、F1取代E0、F0，求第二个轴w2、c2以及第二个成分t2、u2，则

式中：w2、c2分别为对应于矩阵最大特征值的单位特征向量.

于是便得到E1和F1对t2的回归方程

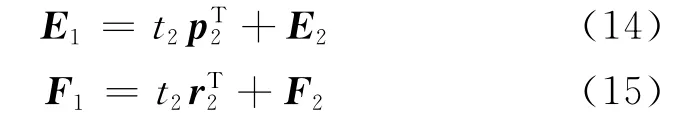
若X的秩是A，则有

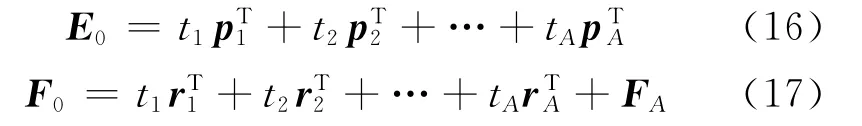
1.3 交叉性验证

在单因变量的偏最小二乘回归中，交叉有效性的定义为：假定yi为原始数据，t1，t2，…，tm是在偏最小二乘回归过程中提取的成分.yhi是使用全部样本点并提取h个成分回归建模后，第i个样本点的拟合值；yh（－i）是在建模时删去样本点i，取h个成分回归建模后，用此模型计算yi的拟合值.

当Qh≥0.097 5时，引进新的主成分th会对模型的预测能力有明显的改善作用.

2 样本数据库

煤灰结渣程度一般按轻微、中等、严重进行评价，此处把轻微、中等、严重结渣模式样本分别记作第1类（记为1）、第2类（记为2）、第3类（记为3），把预测值小于1.5的归为第1类，预测值大于或等于1.5且小于2.5的归为第2类，大于或等于2.5的归为第3类.以适合我国煤种的4个判别指标：灰的软化温度、碱酸比（J＝［m（CaO）＋m（MgO）＋m（Fe2O3）＋m（K2O）＋m（Na2O）］／［m（SiO2）＋m（Al2O3）＋m（TiO2）］）、硅比 （G＝100m（SiO2）／［m（SiO2）＋m（Fe2O3）＋m（CaO）＋m（MgO）］）、硅铝比（S＝m（SiO2）／m（Al2O3））作为输入，以煤灰结渣程度作为输出，建立判断煤灰结渣程度的非线性迭代PLS模式识别预测模型，以期更加全面地考虑结渣影响因素，提高判别的准确性.同时选取已知结渣特性的24个煤灰样本作为训练样本（表1）.表2为13个煤灰测试样本的数据库.

3 方程的拟合

具体主成分提取过程如下：

（1）提取第一个成分

表1 煤灰训练样本数据库Tab.1 Data sets of coal－ash training samples

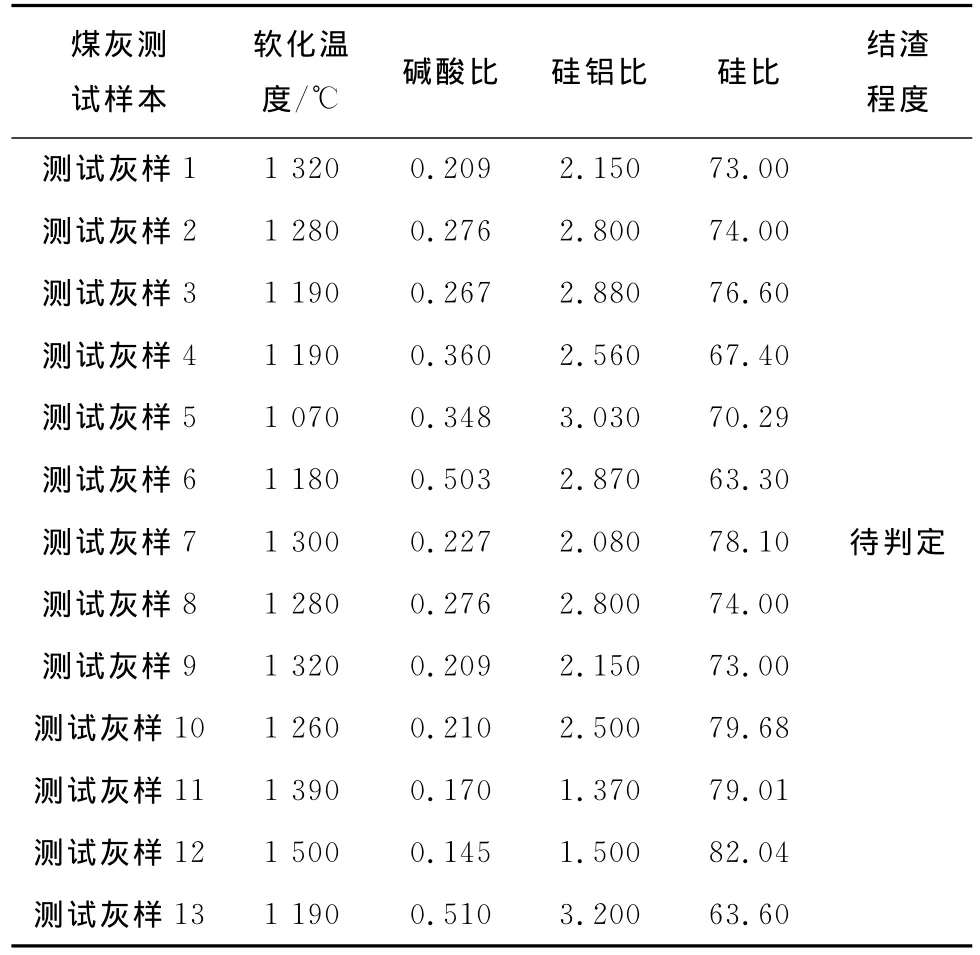
表2 煤灰测试样本数据库Tab.2 Data sets of coal－ash test samples

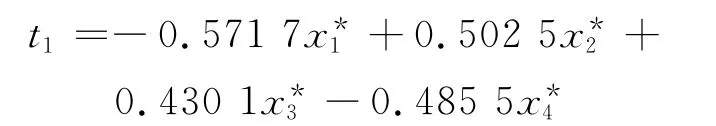
则回归方程为

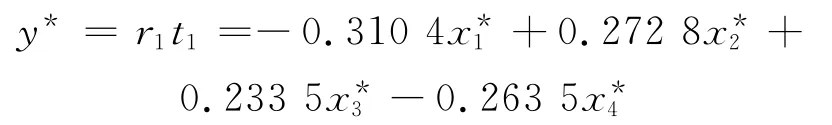
采用交叉验证性原则，此时

Q1＝0.910 5＞0.097 5，继续计算.

（2）提取第二个成分

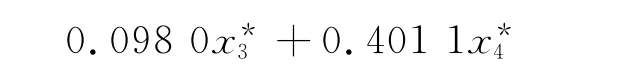
采用交叉验证性原则，此时

Q2＝0.061 8＜0.097 5，停止计算.

因此，当提取1个成分时，模型预测能力最佳.于是可得标准化变量的回归方程为：

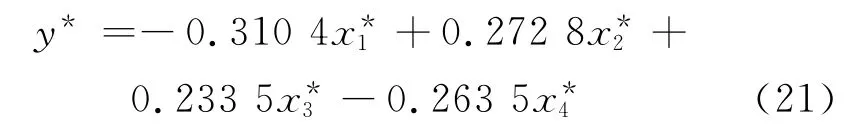
转换为原始变量的偏最小二乘回归方程为：

则此24个煤灰样本的拟合结果见表3.按照之前的结渣程度和预测值的分类原则，所得方程拟合结果与实际结渣程度完全一致，即评判准确率为100%.

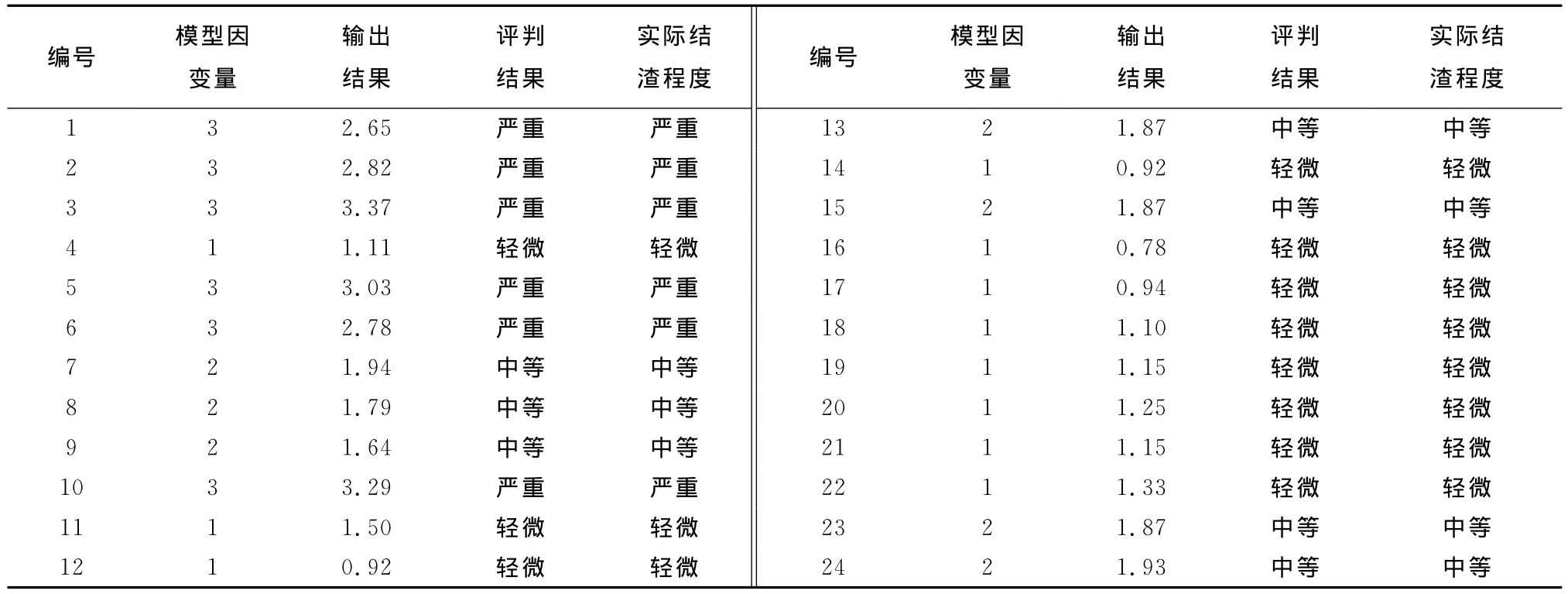
表3 训练样本预测方程评判结果Tab.3 Prediction results of test samples

4 模型的探讨与检验

4.1 指标的同向性与异向性概念

下面给出各指标的评判界限.煤灰软化温度的评判界限为：

t2＞1 390℃，轻微结渣；

t2＝1 260～1 390℃，中等结渣；

t2＜1 260℃，严重结渣；

碱酸比（J）的结渣判断界限为：

J＜0.206，轻微结渣；

J＝0.206～0.4，中等结渣；

J＞0.4，严重结渣；

硅铝比（S）的结渣判断界限为：

S＜1.87，轻微结渣；

S＝1.87～2.65，中等结渣；

S＞2.65，严重结渣；

硅比（G）的结渣判断界限为：

G＞78.8，轻微结渣；

G＝66.1～78.8，中等结渣；

G＜66.1，严重结渣.

由以上评判界限不难看出，对于软化温度、硅比的评判指标，其指标值越大，则结渣程度趋向轻微，依据上文的规定，结渣程度值随着指标值的增大而减小，这种现象称为指标的异向性，该指标称为异向性指标.

对于碱酸比、硅铝比的评判指标，其指标值越大，则结渣程度趋向严重，依据上文的规定，即结渣程度值随着指标值的增大而增大，这种现象称为指标的同向性，该指标称为同向性指标.

4.2 对拟合方程系数的分析

依据上述定义分析拟合阶段所得预测方程式（21）或式（22）.由预测方程式（21）可知，该预测方程中x＊1、x＊2、x＊3、x＊4分别对应软化温度、碱酸比、硅铝比和硅比.

下面分析该预测方程各自变量的系数：软化温度、硅比对应的系数分别为－0.310 4和－0.263 5，碱酸比、硅铝比对应的系数分别为＋0.272 8和＋0.233 5.即异向性指标对应的系数皆为负值，而同向性指标对应的系数皆为正值.也就是说，在所设定的前提条件下，随着各指标值的逐渐增大，其对预测方程的影响是：异向性指标具有削弱结渣程度的作用，而同向性指标具有增强结渣程度的作用.

由式（22）可知，要想煤灰不结渣或者轻微结渣，就应当使y值小于1.5，即使下式成立：

对式（23）进行整理后，可得：

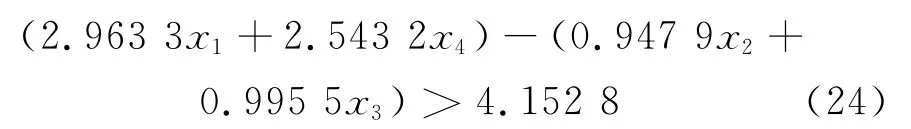
令（2.963 3x1＋2.543 2x4）＝A，（0.947 9x2＋0.995 5x3）＝B，则A、B分别表示异向性指标的和、同向性指标的和.式（24）表明，要降低煤灰的结渣程度，则要满足

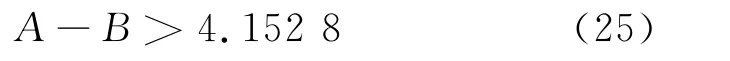
即异向性指标之和与同向性指标之和的差值应大于4.152 8.

4.3 模型的对比验证

为了验证该拟合方程的有效性，将另外13组测试样本代入拟合好的方程中进行检验，测试结果见表4，除第10个样本与实际结果不一致外，其余12个测试样本的方程拟合结果均与实际结果相符，评判准确率为92.3%.

此外，将各测试样本按照前面提到的单一指标评判界限评判，结果见表5.由表5可以看出，软化温度、碱酸比和硅比评判准确率为76.9%，最低的为硅铝比，评判准确率为69.2%.显然这些单一指标的准确率都低于所提出的PLS预测模型.

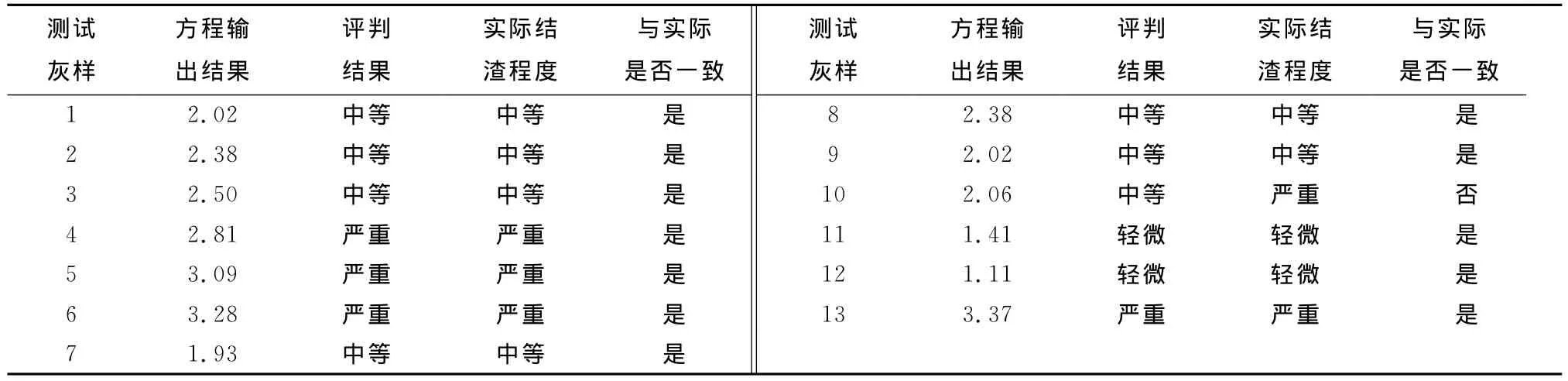
表4 测试样本拟合方程评判结果Tab.4 Prediction results by fitting equation for test samples

表5 测试样本单一指标评判结果Tab.5 Prediction results by single index for test samples

5 结 论

基于偏最小二乘算法和交叉验证理论，建立了煤灰结渣特性预测方程，通过对已知和待判样本的预测评判，PLS预测模型的预测精度远高于单一评判指标，因此，所建模型是合理可行的；与此同时，提出指标的同向性和异向性概念，通过对拟合方程的分析，给出了煤灰结渣特性的评判依据.

［1］CHEN Lijun，WEN Xiaoqiang，WANG Gong，et al.A summary of prediction methods for slagging properties coal－fired boilers［J］.Thermal Power Generation，2006，35（6）：1－18.

［2］HE Peiao，ZHANG Zhongxiao.Experimental study of China＇s power coal slagging characteristics［J］.Power Engineering，1987，7（2）：1－11.

［3］LI Wenyan，KANG Zhizhong，SONG Zhiping.Development of slagging prediction technique for pulverized coal－fired boiler and application of new techniques in this field［J］.Electric Power，2003，36（2）：12－15.

［4］李永兴，陈春元.动力用煤结渣特性综合判别指数的研究［J］.热力发电，1994，23（3）：36－39.LI Yongxing，CHEN Chunyuan.Study of the slagging property of the coals of comprehensive discriminant index ［J］.Thermal Power Generation，1994，23（3）：36－39.

［5］QIU Jianrong，MA Yuyi.Grey clustering judgment on performance of coal［J］.J Huazhong Univ of Sci and Tech，1994，22（3）：52－55.

［6］冯宝安，撒应禄.电站锅炉用煤常规结渣指标的模糊综合评判［J］.锅炉技术，1996，27（5）：13－16.FENG Baoan，SA Yinglu.A study of conventional slagging indicator in power plant based on fuzzy multifactorial decision［J］.Boiler Technology，1996，27（5）：13－16.

［7］FENG Baoan.Fuzzy multifactorial decision for coal slagging property judging ［J］.Boiler Technology，1997，28（3）：21－25.

［8］LIU Boqian，WANG Yuan，LI Jinfeng.Fuzzy analysis of combustion characteristics of Yuanbaoshan lignite［J］.Journal of Northeast China Institute of Electrical Power，1998，18（2）：80－84.

［9］LIU Gehui，ZHENG Chuguang，LIU Yinghui.Application of adaptive fuzzy neural network to the forecast of coal slagging in power plants［J］.J Huazhong Univ of Sci and Tech，2000，28（3）：108－110.

［10］WANG Binzhong，WU Zhansong，XU Lidong，et al.Forecasting slagging characteristic of coal ash using fuzzy neural network method［J］.J Tsinghua Univ：Sci and Tech，1999，39（4）：104－107.

［11］XIAO Jun，LÜZhenzhong，WANG Jun，et al.A model for the diagnosis of coal ash slag－buildup characteristics by using an improved BP algorithm ［J］.Journal of Engineering for Thermal Energy and Power，2002，17（3）：271－274.

［12］GUO Jia，ZENG Hancai.Coal slagging characteristics recognition by fuzzy mathematics for coal－fired power plants［J］.Thermal Power Generation，1994，23（2）：4－6.

［13］ZHAO Limin.Comprehensive fuzzy assessment of slagging in utility boilers furnaces［J］.Thermal Power Generation，1998，27（5）：8－10.

［14］XUE Guisheng，DING Weiming，CHENG Li.Slag characteristic valuation based on supporting vector machine［J］.Energy Research and Utilization，2008，20（6）：13－15.

［15］DING Shifei，SHI Zhongzhi，JIN Fengxiang.Information pattern recognition algorithm based onnonlinear iterative PLS［J］.Computer Engineering，2008，34（1）：20－22.