长叶片相邻围带或凸肩接触转速计算方法

陈德祥， 徐自力， 曹守洪， 范小平， 吴其林

（1.西安交通大学 航天学院，机械结构强度与振动国家重点实验室，西安710049；2.东方汽轮机有限公司，德阳618000）

成圈叶片只有在“三重点”条件下才会产生共 振，在固有频率和气流激振力频率相等而不满足“三重点”的振型条件下，叶片并不会产生共振［1－2］，因此现代汽轮机动叶中的长叶片多采用围带或围带加凸肩的结构（图1），使叶片在工作时处于自锁的成圈状态.叶片围带有2种成圈方式：一是采用预扭设计［3］，这种方式采用的围带几何形状能使叶片装配完成后相邻的叶片围带相互接触并挤压；二是采用间隙设计［4－6］，这种方式初始状态下相邻围带之间存在一定的间隙，随着转速的加快，叶片发生扭转恢复，最终使围带相互接触并挤压（图2）.第二种方式下，叶片在装配以及更换时比预扭叶片简单.

图1 低压末级叶片Fig.1 Low－pressure last－stage blade

图2 叶片扭转恢复引起的围带接触Fig.2 Shroud contact caused by blade untwisting

理论上，围带或凸肩之间的接触法向力或接触应力定量地反映了叶片的压紧程度和成圈性，是叶片设计中的重要参数之一，它的取值一方面与其所遵从的设计理念有关，是侧重于成圈整体性还是侧重于摩擦阻尼减振性，另一方面也与叶片的长度、工作条件有关.但是接触法向力或接触应力的大小难以在试验中直接测量.一般可通过测量安装完成后的围带预扭角度来确定预扭设计叶片围带的压紧程度，但对间隙设计的叶片只有在转动状态下才形成成圈结构，叶片之间的扭转角度无法通过试验直接测量.围带开始接触时的转速宏观上反映了间隙设计叶片相邻围带之间的压紧程度，进而反映了叶片的自锁成圈性，叶型一定时接触转速越小，则工作状态下接触面上相互挤压越紧.重要的是，接触转速可以通过试验进行测量，表现在坎贝尔图上接触转速点的频率发生跳跃.接触转速的测量值与设计值的符合程度反映了该级叶片的整体制造质量，因此计算围带开始接触时的转速对设计成圈叶片有着重要意义.

笔者用接触法向力来表征相邻围带或凸肩之间的接触关系，并通过迭代计算成圈叶片的接触转速.在给定转速下，影响相邻围带或凸肩上接触法向力的因素复杂，难以给出其表达式，而带接触的三维有限元分析能考虑各种复杂因素［7－9］，故通过三维接触有限元分析获得相邻围带或凸肩上的接触法向力.根据整圈叶片几何上具有循环对称的特点，利用循环对称算法来降阶［10－11］，即通过计算1个扇区来获得整圈的结果.由于通过三维接触有限元分析只得到接触法向力的函数值，没有导数值，并且接触法向力在未接触时一直为0，所以牛顿法或割线法迭代不适用，故采用二分法进行接触转速的计算.每迭代一次需要进行一次有接触的三维有限元分析，取上一次有限元分析的结果作为本次有限元分析初始值来提高收敛速度.

1 围带、凸肩接触转速的计算方法

1.1 相邻围带、凸肩之间关系的量化表征

相邻围带之间关系包括相互分离和相互接触2种状态，分离状态下可用相邻围带之间的间隙d来表征，接触状态下可用围带之间的法向相互作用力F来表征（图2）.叶片的扭转恢复主要是由离心力引起的，并且随着转速的加快而增加，因此d和F都是转速的函数，即d＝d（ω），F＝F（ω），他们随转速变化的趋势如图3所示.当ω＜ωc时，相邻围带间隙随着转速加快单调减小，法向作用力保持为0；当ω＞ωc时，法向作用力随转速加快单调增大，而间隙值保持为0，所以围带接触转速为：

图3 围带之间接触关系表征量随转速的变化Fig.3 Variation of characteristic parameters of shroud with rotational speed

根据围带之间接触状态的量化表征，确定围带接触转速最终归结为寻找d（ω）＝0的最小根，或者寻找F（ω）＝0的最大根.相邻凸肩之间关系与围带的情况完全相同.

1.2 计算方法

影响相邻围带、凸肩间隙和接触法向力大小的因素复杂.首先，离心力与转速为平方关系，间隙和接触法向力随转速非线性变化；其次，围带、凸肩以及叶根处存在接触，接触问题本身具有非线性，并且接触状态受离心力的影响；再次，末级叶片一般柔度大，这导致几何非线性问题；最后，如果叶片上同时有围带和凸肩结构，它们相互之间也有影响.因此，图3为间隙和接触法向力随转速的变化趋势，但无法表达成转速的函数.

笔者采用考虑接触的三维有限元方法确定某一给定转速下间隙或接触法向力的值.但通过有限元计算只能得到间隙或接触法向力的函数值，一般没有导数信息，因此迭代中需要用到导数的梯度类算法，牛顿法不能用于该问题的求解.另外，从图3可以看出，不论采用间隙还是接触法向力进行迭代，在全转速范围内方程d（ω）＝0或F（ω）＝0的根不是唯一的，应用非梯度类算法中的割线法能计算出其中的一个根，但不能得到d（ω）＝0的最小根或F（ω）＝0的最大根，因此割线法也不适用于该问题的求解.二分法不要求导数信息，也没有割线法的问题，适用于接触转速的迭代计算.

虽然理论上间隙值和接触法向力都可以用于迭代计算，最终的收敛结果是相同的.但是进入接触之后，围带、凸肩的间隙都为0，间隙值不能反映成圈性的变化，而接触法向力则可以直接反映压紧程度，比间隙值更有工程价值，因此对接触法向力进行迭代计算，其算法流程图见图4.

假定ωc所在的转速区间是（ωa，ωb），采用二分法计算时，每迭代一次，ωc所在转速区间长度减小一半，直到转速区间的长度满足给定的收敛条件.收敛条件为：

式中：ωn为工作转速；ωa、ωb分别为ωc所在转速区间的上、下界；ε为给定的正常数.

2 算例

2.1 计算对象及有限元网格

图4 采用二分法计算接触转速流程图Fig.4 Bisection iteration of contact speed calculation

采用以上方法计算某200MW机组末级动叶片围带和凸肩的接触转速.叶片长度为816mm，同时具有围带和凸肩结构（图1），围带之间间隙为0.5 mm，凸肩之间间隙为0.2mm.利用循环对称特点，取整级叶片和轮盘的1个扇区（图5（a））进行计算，计算中考虑相邻凸肩之间的接触（图5（b））、相邻围带之间的接触（图5（c））以及叶根与轮盘之间的接触（图5（d））.因为需要考虑围带和凸肩的接触，所以叶片上的循环对称面选在叶片内部，先对整个叶片进行网格剖分，然后将围带和凸肩上的一部分网格转动1个扇区，转动之后自然形成逐点匹配的循环对称节点.采用8节点6面体单元进行空间离散，单元总数为127 929个，其中叶片划分了92 929个单元，轮盘划分了35 000个单元；节点总数为148 360个，其中叶片节点数为106 150个，轮盘节点数为42 210个.

2.2 计算结果

取收敛条件为ε＝0.01，围带、凸肩接触转速的迭代收敛过程见表1和表2.从表中可以看出，在迭代过程中，区间（ωa，ωb）的下限和上限分别从小于接触转速和大于接触转速的两侧向接触转速收敛.当接触力法向为0时，接触转速所在区间的下限逐渐增大；当接触力法向大于0时，接触转速所在区间的下限、上限均逐渐减小，对应的接触法向力也逐渐减小.将收敛时转速区间的平均值作为接触转速，从表中可得到围带的接触转速为738r／min，凸肩的接触转速为1 184r／min.虽然该叶片围带间隙大于凸肩间隙，但围带比凸肩先进入接触状态.该叶片在工作转速下围带和凸肩接触法向力最大，对应在围带上的平均接触应力为14.5MPa，凸肩上的平均接触应力为18.5MPa.

图5 某200MW机组低压末级叶片、轮盘模型Fig.5 Meshing of a low－pressure last－stage blade and disk for a 200MW unit

表1 计算围带接触转速的二分法迭代过程Tab.1 Bisection iteration process of shroud contact speed calculation

根据围带、凸肩每一次迭代的计算结果，给出围带、凸肩上的接触法向力随转速（300～1 500 r／min）的变化情况，结果见图6.由于围带接触比凸肩接触出现得早，从围带进入接触到凸肩进入接触的这一过程中，离心力产生的扭转恢复力矩与围带之间法向力产生的力矩平衡，围带上的法向力单调增大.当凸肩进入接触后，一部分扭转恢复力矩与凸肩法向力产生的力矩平衡，因此围带上的法向力随转速加快而增大的速度在此时有所减小.

表2 计算凸肩接触转速的二分法迭代过程Tab.2 Bisection iteration process of lacing contact speed calculation

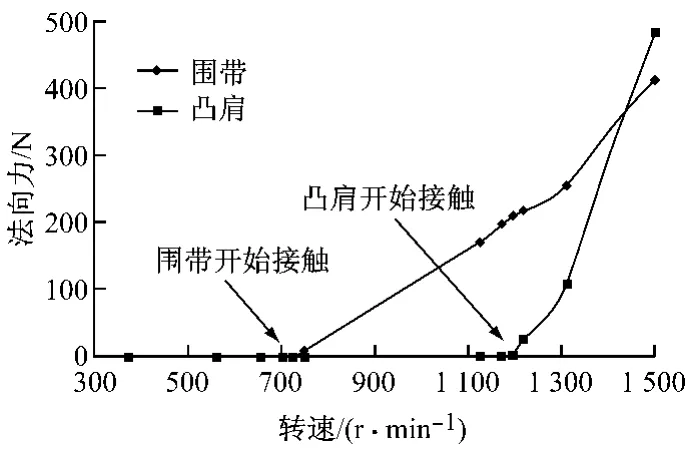
图6 某低压末级叶片围带、凸肩上接触法向力随转速的变化Fig.6 Variation of normal contact force with rotational speed of shroud and lacing on a low－pressure last－stage blade

3 计算速度和收敛条件分析

以上方法的最大计算成本在于三维接触有限元计算，对所研究的叶片共进行了8次有限元计算，包括迭代开始之前工作转速下的一次有限元计算.接触问题具有非线性特点，其求解过程通常需要进行迭代，非线性问题的迭代收敛速度与初始值选择有关，初始值越接近真实解其收敛速度越快.由于上一次迭代已经在某一转速下达到平衡状态，其计算结果比任意给定的一组值更接近本次迭代转速下的真实解，因此笔者将上一次有限元计算结果作为本次接触有限元迭代的初始值.采用8核CPU，16G内存计算机进行计算，围带或凸肩接触转速的迭代计算过程需7h，其中第一次接触有限元分析需2h，之后每次接触有限元分析约43min，计算速度显著加快.

采用二分法迭代k次后，解所在区间的长度是初始区间长度的1／2k.对工作转速为3 000r／min的机组，取收敛条件ε＝0.01，需要迭代7次，收敛时接触转速所在区间的长度为23.4r／min，取ωc＝（ωa＋ωb）／2，则接触转速的计算误差小于11.7r／min.如果将收敛条件提高一个量级，取ε＝0.001，这时需要迭代10次，接触转速的计算误差小于1.5 r／min.由于ε＝0.01给出的计算精度基本满足描述成圈性对精度的要求，且当法向力很小时，三维接触有限元计算的误差成为主要因素，增加迭代次数并不能提高计算精度，反而增加计算成本，因此，并非迭代次数越多越好，ε＜0.001是不必要的.笔者建议迭代收敛条件在0.01～0.001之间，即整个计算过程迭代7～10次.

4 结 论

汽轮机末级长叶片围带、凸肩的接触转速反映了整级叶片的成圈性，对叶片成圈性的定量评价具有重要意义.用接触法向力来表征相邻围带、凸肩的接触关系，采用二分法计算围带和凸肩的接触转速.迭代中取上一次迭代的有限元分析结果作为本次迭代中接触有限元分析的初始值，提高了迭代的收敛速度.计算接触法向力时采用的三维有限元法考虑了离心力、接触非线性、几何非线性、围带和凸肩相互作用等多种因素的影响，具有较高的计算精度.应用上述方法对某200MW汽轮机组末级叶片围带、凸肩的接触转速进行了计算，经过7次迭代，接触转速的计算误差小于11.7r／min.本文方法可用于长叶片设计中相邻围带或凸肩接触转速的计算.

［1］HUANG W H.Free and forced vibration of closely coupled turbomachinery blades［J］.AIAA Journal，1981，19（7）：918－924.

［2］徐芬，程凯，彭泽瑛.围带结构对整圈自锁叶片振动特性的影响［J］.动力工程学报，2010，30（5）：347－351.XU Fen，CHENG Kai，PENG Zeying.Influence of shroud configuration on vibration characteristics of the full circle self－lock blade［J］.Journal of Chinese Society of Power Engineering，2010，30（5）：347－351.

［3］杨鑫，马艳红，洪杰.基于接触状态的叶冠预扭设计［J］.航空发动机，2008，34（4）：11－15.YANG Xin，MA Yanhong，HONG Jie.Pretwisted design of shroud at contact state［J］.Aeroengine，2008，34（4）：11－15.

［4］KANEKO Y，MORI K，OHYAMA H.Development and verification of 3 000rpm 48inch integral shroud blade for steam turbine［J］.JSME International Journal Series B，2006，49（2）：205－211.

［5］KANEKO Y，OHYAMA H.Analysis and measurement of damping characteristics of integral shroud blade for steam turbine［J］.Journal of System Design and Dynamics，2008，2（1）：311－322.

［6］FUKUDA H，OHYAMA H，MORI TMK，et al.Development of 3，600－rpm 50－inch／3，000－rpm 60－inch ultra－long exhaust end blades［J］.Mitsubishi Heavy Industries Technical Review，2009，46（2）：18－25.

［7］PAPANIKOS P，MEGUID S，STJEPANOVIC Z.Three－dimensional nonlinear finite element analysis of dovetail joints in aeroengine discs［J］.Finite Elements in Analysis and Design，1998，29（3／4）：173－186.

［8］MEGUID S，KANTH P，CZEKANSKI A.Finite element analysis of fir－tree region in turbine discs［J］.Finite Elements in Analysis and Design，2000，35（4）：305－317.

［9］BEISHEIM J，SINCLAIR G.On the three－dimensional finite element analysis of dovetail attachments［J］.Journal of Turbomachinery，2003，125（2）：372－378.

［10］张锦，刘晓平.叶轮机振动模态分析理论及数值方法［M］.北京：国防工业出版社，2001.

［11］董广明，陈进，孟庆集.循环对称算法及其在汽轮机叶盘系统振动分析中的应用［J］.振动工程学报，2004，17（z1）：126－129.DONG Guangming，CHEN Jin，MENG Qingji.Cyclic symmetry algorithm with its application in vibration analysis of turbine bladed discs［J］.Journal of Vibration Engineering，2004，17（z1）：126－129.