改进的基于两个矩阵的关联规则挖掘算法
曹风华
(内蒙古财经学院计算机信息管理学院,内蒙古 呼和浩特 010070)
关联规则挖掘作为数据挖掘的一个重要研究分支,主要研究从大型数据集中发现隐藏的、有趣的、属性间存在的规律。由于关联规则挖掘的对象通常是包含有海量原始数据和大量项目的事务数据库,因此如何提高从大型数据库中挖掘关联规则的效率和伸缩性,以便有效降低计算的复杂性、提高算法的运行速度,仍是关联规则挖掘研究领域的核心问题。
R.Agrawal等人首先提出了挖掘关联规则的Apriori算法[1-2],该算法是挖掘布尔关联规则最有影响的数据挖掘算法之一,其基本思想是重复扫描数据库,根据一个频繁集的任意子集都是频繁集的原理,可以从长度为k的频繁项集迭代地产生长度为k+1的候选项集,再扫描数据库以验证其是否为频繁项集。该算法因多次扫描规模不变的事务数据库,耗费大量时间,随后出现了很多类Apriori算法,其中有些算法将事务数据库以二进制形式映射到内存中然后进行相关挖掘操作,这类算法由于减少了直接扫描数据库的次数,避免了在I/O操作上浪费大量时间,在一定程度上提高了挖掘效率。
文献[3]中提出了一种高效的 ABM(Algorithm Based on Matrix)算法,该算法具有前文所述类Apriori算法的优点,但每次操作的对象都是规模不变的向量,而事实上,当项集维数很高时,参与运算向量的规模将在一定程度上影响算法的执行效率,因此,在ABM算法的基础上,文中提出了改进的 ABTM(Algorithm Based on Two Matrix)算法,在算法中引入了两个矩阵,一个用来映射数据库,另一个用来存储频繁2-项集相关信息。通过对两个矩阵的操作,有效避免了Apriori算法中需要多次重复扫描规模不变的数据库和产生大量候选集并进行剪枝的缺点,并解决了ABM算法中影响算法执行效率的瓶颈问题,实验表明,本算法具有较好的性能。
1 相关概念和性质
设 I={i1,i2,…,im}是全体数据项的集合,数据项集是指由不同数据项构成的非空集合。设D为全体事务集,每条事务T有惟一标识TID,且T⊆I。对于项集X⊆I,当且仅当X⊆T时称项集X在事物T中出现。项集X在事务集合D中出现的次数称为X的支持数,记做sup(X)。对于用户给定的最小支持数阀值min_sup,若sup(X)≥min_sup,则项集X是频繁项集,否则X是非频繁项集。若频繁项集X有k个数据项组成,则称X是频繁k-项集,所有频繁k-项集的集合记做Lk。
性质1 频繁k-项集的所有m,0<m<k,维子集都是频繁项集。
性质2 m维非频繁项集的任一k,k>m,维超集是非频繁项集。
性质1和性质2的详细证明可参见文献[3]。
推论:项集{i1,i2,…,ik,iu},k≥2,i1< i2< … <ik<iu)为频繁k+1项集的必要条件是:(1){ij,iu},j=1,2,…,k必须都为频繁2-项集。(2)能与iu组成频繁2-项集且小于iu的项的个数至少要有k个。
证明:{i1,i2,…,ik,iu}为频繁 k +1 项集,对于 j =1,2,…,k,2 项集{ij,iu}共有 k 个且都是项集{i1,i2,…,ik,iu}的子集,由性质1知,这k个2项集都是频繁项集,同时可能存在 k <j<u,ij< iu且{ij,iu}是频繁 2项集,所以能与iu组成频繁2-项集且<iu的项的个数至少有k个。
性质3 ∀i∈I,如果i在频繁k-1项集的集合Lk-1中的出现次数<k-1,则 i 不会出现在任何频繁k-项集中。
证明:假设项目i出现在某频繁k-项集中,由于该频繁k-项集有k个k-1维子集,且k个子集都在Lk-1中,因此对于i,在这k个k-1维子集中共出现k-1 次,故≥k-1,与条件矛盾,因此i不会出现在任何频繁k-项集中。
根据频繁k-项集的支持数的定义很容易得出结论,证明略。
2 ABTM算法描述
(1)构造事务矩阵TM(Transaction Matrix),并产生频繁1-项集。对于有m条事务,n个项的事务数据库,建立一个 m × (n+1)的事务矩阵[8]TMm×p,p=n+1,并将矩阵每位元素初始化为0。扫描事务数据库,统计每个项目出现的次数,同时如果项目i在第j条事务中出现,则将Mji置1,否则置0。矩阵的第n+1列为hcount列,该列记录每行中1的个数,每行的hcount值表示该条事物中项目的个数,也即该事务的长度。矩阵前n列分别是与项目i对应的位向量BVi,某列中1的个数即是该列对应的项目的支持数,如果该值大于最小支持数,则该项目是频繁1-项集。
(2)构造二项支持矩阵SM(Support Matrix),产生频繁2-项集。建立一个n×(n-1)的矩阵SMn×q,n为项目数,q=n-1,并将矩阵每位元素初始化为0。将频繁1-项集中的项目进行排序后(本文使用字典序),对所有项目i,取比i大的项目j,对它们对应的向量做内积运算[5-6],即如果 B Vi·BVj不小于最小支持数,则项集{i,j}是频繁2-项集,将 S Mij置1,否则置0。矩阵的第n行为vcount行,该行记录每列中1的个数,每列的vcount值表示能与该列对应的项组成频繁2-项集且编号小于该项的项的个数。
(3)裁剪事务矩阵TM[3]。在求频繁k-项集前,计算各单项在Lk-1中的出现次数,根据性质3,若<k-1,则删除i在矩阵中对应的列。重新计算矩阵的hcount列的值后,根据性质4,如果某行的hcount值<k,则删除该行。
(4)求频繁k-项集。K-项集的产生是通过对频繁k-1项集的扩展来求解的,对于频繁k-1项集{i1,i2,…,ik-1},i1<i2< … < ik-1,如果在二项支持矩阵中有 SM[ik-1,iu]=1,iu> ik-1,iu列的 vcount值不小于k -1,且 SM[i1,iu]=SM[i2,iu]= … =SM[ik-2,iu]=1,那么扩展该频繁k-1-项集为 k-项集{i1,i2,…,ik-1,iu},对这k个项目对应的映射矩阵中的列向量做内积运算,即如果 BVi1·BVi2·…·BVik-1·BViu的结果不小于最小支持数,则项集{i1,i2,…,ik-1,iu}是频繁k-项集。
(5)重复执行算法的第(3)~(4)步,直至不能产生更高阶的频繁项集。
3 算法执行实例
以表1所示的事务数据集为例,介绍ABTM算法的执行过程,设最小支持数min_sup=2,具体过程如下:

表1 事务数据集
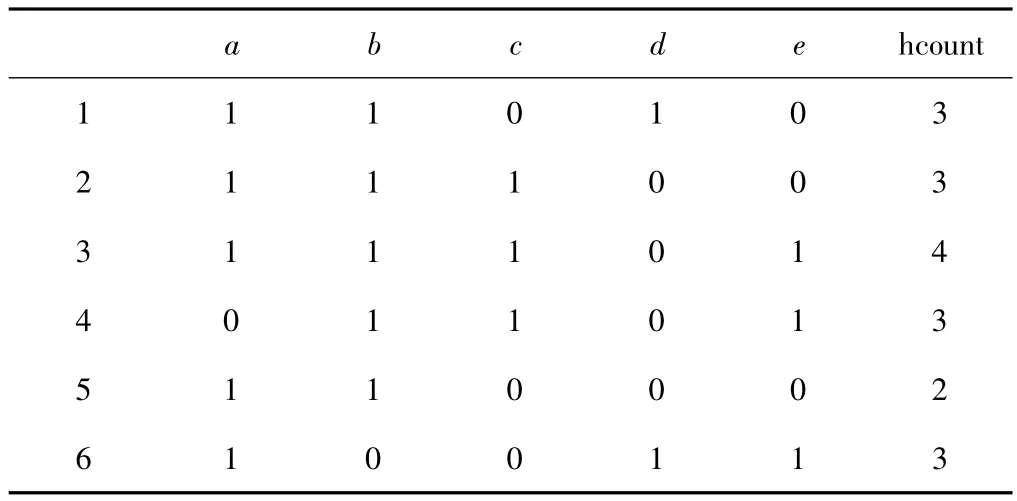
表2 事务矩阵TM

表3 支持矩阵SM
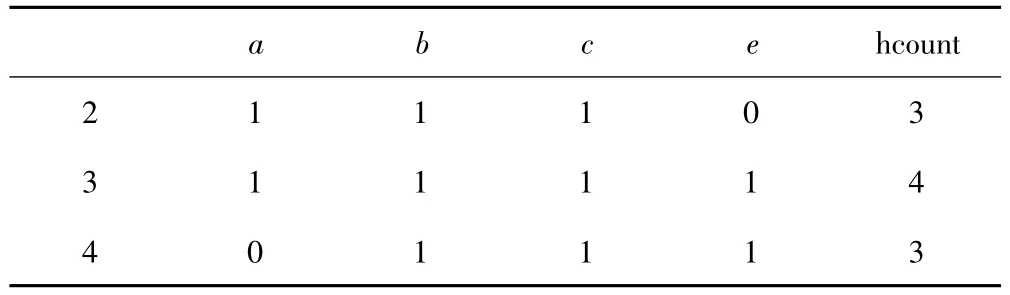
表4 裁剪后的TM矩阵
第一步 扫描事务数据集构造映射矩阵,如表2所示。得到 L1={a,b,c,d,e}。
第二步 构造二项支持矩阵,如表3所示。得到L2={{a,b},{a,c},{a,d},{a,e},{b,c},{b,e},{c,e}}。
第三步 对于L2中的各单项,由于=1<2,因此删除矩阵的d列,对hcount重新计算,由于1,5,6行的hcount都<3,删除这3行,得到裁剪后的矩阵,如表4所示。
第四步 根据频繁2-项集中的项和二项支持矩阵记录的相关信息,可以得到扩展3-项集{a,b,c},{a,c,e}和{b,c,e},由映射矩阵可得到 BVa·BVb·BVc=2,BVa·BVc·BVe=1,BVb·BVc·BVe=2,因min_sup=2,得到 L3={{a,b,c},{b,c,e}}。由于 L3中项的个数<3,故L3是最大频繁集。
4 算法比较和实验结果
4.1 算法性能比较
Apriori算法是挖掘关联规则的经典算法,与该算法相比,ABTM算法仅需要扫描数据库一遍,减少了读取数据库的时间,而且频繁k-项集的产生是通过扩展项集和向量内积运算求解,不需要连接和剪枝等操作。Apriori算法操作的对象直接是事物数据库,而且每次扫描数据库的规模不变,ABTM算法通过转换将数据库映射到矩阵中以二进制形式存储,通过合理设计稀疏矩阵的数据结构,使最终占用空间相对较小。
ABM算法[3]是一种高效的关联规则挖掘算法,与该算法相比,ABTM算法的不同之处在于两个方面:(1)采用矩阵映射事务数据库,而不是建立单个项目的位向量,尽管两种算法将数据库映射到内存中占用的空间相同,但矩阵存储能够实现对规模的有效裁剪,随着项集维数的增长,ABTM算法将矩阵中无用的行和列删除,使得内存空间逐步得到释放,同时参与运算向量的长度越短,计算量也越小。(2)ABM算法中的支持矩阵是(n-1)×n的,但考虑到最小项目不可能与更小的项目构成频繁2-项集,因此无需为最小项目建立对应的列,所以ABTM算法采用的是(n-1)×(n -1)矩阵,节省了存储空间[8]。
4.2 实验结果与分析
算法采用Java实现,数据库为SQL Server2000,实验机器CPU为Intel Pentium42.8 GHz,内存为512 MB,测试数据集有10000条事务,由IBM数据生成器生成,该数据生成器可以在IBM网站下载。
为比较提出的ABTM算法和经典算法在不同支持度下的所用时间,设置了不同的支持度分别运行各算法,描点绘图如下,得到的实验结果如图1所示。
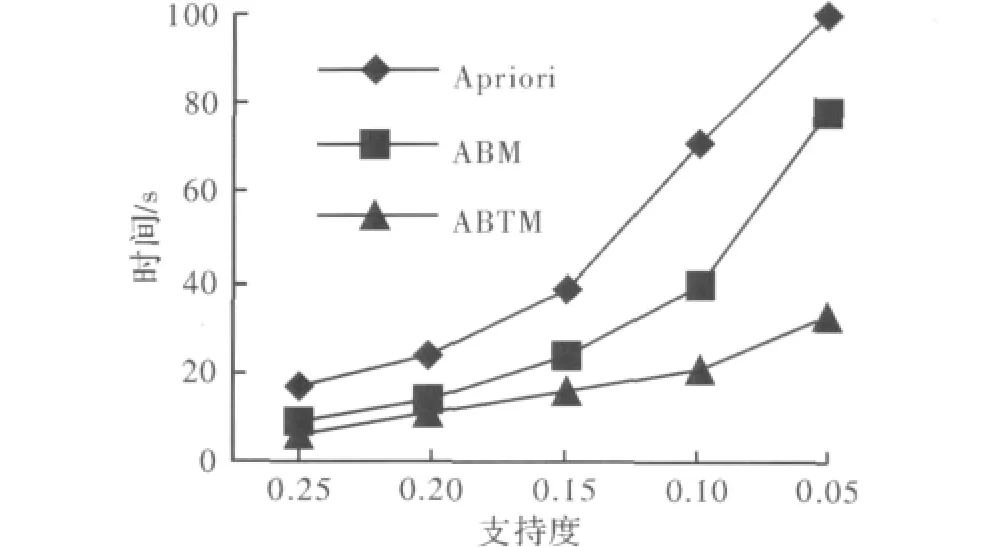
图1 不同支持度下个算法运行时间
由于提出的算法和ABM算法性能的差异取决于候选项集的产生速度以及产生数量的大小,而属性数量的多少直接影响了候选项集的生成。设置支持度固定为0.15,针对不同的属性个数,分别统计各算法的所用时间,绘图如2所示。
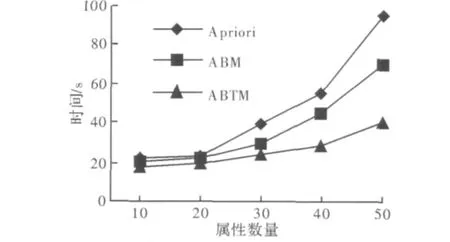
图2 属性数量对算法的影响
从图2可以看出,ABTM算法运行所需时间显著少于Apriori算法和ABM算法。图1中,随着所设定的支持度越来越小,Apriori算法和ABM算法总运算量与支持度呈非线性增长,所需时间也大大增加,而由于ABTM算法仅需要扫描数据库一遍,减少了读取数据库的时间,而且频繁k-项集的产生是通过扩展项集和向量内积运算求解,不需要连接和剪枝等操作,随支持度减小,算法所需时间并未显著增加。图2中,随着属性数量的增加,Apriori算法和ABM算法运行时间迅速上升,而ABTM的扩展项集和向量内积运算并不会因为属性数量增加而收到较大影响。
5 结束语
文中算法引入两个矩阵,分别从时间和空间上进行优化,使得算法效率显著提高,是一种易理解且可行性较好的算法。算法还可以在以下两方面做进一步的优化:(1)由于在构造事务矩阵后就完成了频繁1-项集的产生,所以可以在构造二项支持矩阵前进行一次映射矩阵的裁剪。(2)由于可能存在一些项并非频繁1-项集,那么这些项不可能再出现在更高阶的频繁项集中,因此在构造二项支持矩阵时也没有必要考虑这些项。
[1]戴新喜,白似雪.一种高效的基于模式矩阵的Apriori改进算法[J].广西师范大学学报,2007,25(4):176 -179.
[2]HAN Jiawei,MICELINE K.数据挖掘概念与技术[M].范明,孟小峰,译.北京:机械工业出版社,2001.
[3]牛小飞,石冰,卢军,等.挖掘关联规则的高效ABM算法[J].计算机工程,2004,30(11):118 -120.
[4]王柏盛,刘寒冰,靳书和,等.基于矩阵的关联规则挖掘算法[J].微计算机信息,2007,54(53):144 -146.
[5]刘晓玲,李玉忱.一种利用逻辑“与”运算挖掘频繁项集的算法[J].科技论坛,2005(15A):122-123.
[6]刘以安,刘强,邹晓华.基于向量内积的关联规则挖掘算法研究[J].计算机工程与应用,2006,21(3):172 -174.
[7]曾万聃,周绪波,戴勃,等.关联规则挖掘的矩阵算法[J].计算机工程,2006,32(2):45 -47.
[8]徐章艳,刘美玲,张师超,等.Apriori算法的三种优化方法[J].计算机工程与应用,2004,40(36):190 -192.

