基于PTS抑制OFDM系统PAPR低复杂度算法
邬佳佚,陈建春
(西安电子科技大学电子工程学院,陕西 西安 710071)
OFDM(Orthogonal Frequency Division Multiplexing)技术的一个主要缺点就是会出现较高的PAPR(Peak-To-Average Power Ratio)。与单载波系统相比,OFDM系统内发射信号的瞬时功率波动范围比较大,这就要求系统内的功率放大器、数模转换器以及模数转换器等器件具有较大的线性动态范围。否则,一旦动态范围较大的发送信号进入这些器件的非线性区,就会产生非线性失真,造成子信道间的干扰,进而影响OFDM系统的性能。为解决这个问题,多数学者提出能够有效降低PAPR的各种方法,例如限幅类技术[1]、编码类技术[2]和概率类技术[3-4]。其中概率类技术中的 PTS(Partial Transmit Sequence)方法是一种不会引入失真并且具有理想峰值抑制效果的PAPR抑制技术,因而受到广泛关注。J.B.Huber和S.H.Muller提出的最优化 PTS[4](Optimum PTS,OPTS)计算出全部相位旋转因子组合所对应的信号峰均比值,然后采用全搜索法得到使得PAPR值最小的一组相位旋转因子组合。整个过程中需要大量的运算,致使其算法复杂度非常高。因此Leonard J.Cimini提出了迭代PTS(Iterative PTS,IPTS)[5]为基础,通过控制相位旋转因子序列的搜索空间来减少迭代次数,进而平衡算法的PAPR抑制性能和复杂度。多数的文献[6-8]针对IPTS提出改进方法。文中提出一种在寻找最优相位旋转因子过程中利用抽样序列替代部分传输序列来降低PTS复杂度的方法,并对该算法进行性能仿真。
1 传统的PTS方法
1.1 PAPR的定义
OFDM是个多载波系统,其信号在时域上表现为N个正交子载波信号的叠加。通常将一段时间内,最大峰值功率与平均功率的比值称为峰平比(PAPR)。
假定OFDM系统有N个子载波,则信号可以表示为

其中,X(k),k=0,1,…,N -1 为调制后的数据;WN是相互正交的子载波;x(n)为经过OFDM系统后的输出时域信号。信号的PAPR可以表示为
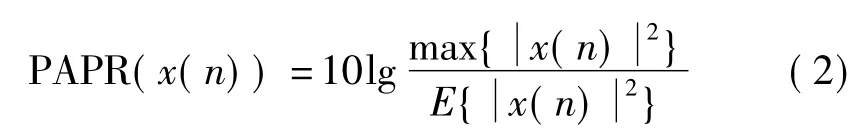
其中,max{}表示计算最大值;E{}表示计算均值。
1.2 传统的PTS算法
设子载波数为N,定义OFDM系统的输入数据为X=[X(0),X(1),…,X(N -1)],把向量 X 分割为 M组互不重叠的子向量,表示为{Xm,m=1,2,…,M},假设每个分组中包含的子载波数目相同。然后将这M个分组按如下方式相加

其中,{bm=ejφm,m=1,2,…,M}是加权系数,并且相位因子φm满足[0,2π)上的均匀分布。然后对X进行IFFT变换,得到
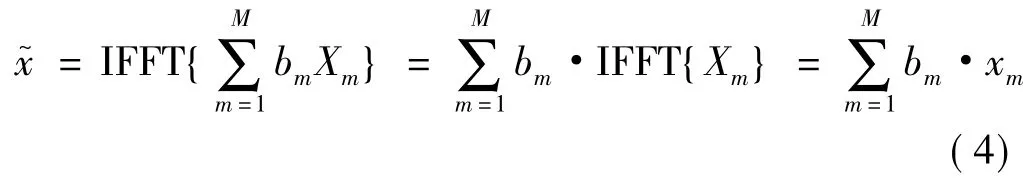
通过选择适当的bm使得PAPR达到最小,同时相应的相位因子序列也作为辅助信息传送给接收端,得到最终的传输数据。
相位因子φm可以在[0,2π)内取任意值,但是一般是在一个离散的相位集合中取值,例如在W个相位值中选取。文献[9]指出,φm可以取固定的值{0,π/2,π,3π/2}。不失一般性,通常固定第一个分组的相位因子为1,则对于分割为M个子序列组的PTS方法而言,根据相位因子的不同组合可以得到WM-1种备选信号。
2 改进的低复杂度PTS方法
传统PTS算法中,需要计算M个N点IFFT变换,和在WM-1个备选信号中搜索PAPR最低的备选信号。在寻找最优相位因子序列时需要进行大量的运算,这就使得PTS方法的运算量成为一个主要缺点。文中提出改进的低复杂度PTS方法可以明显减少寻找最优相位因子的计算量。
在文献[10]中提出相位因子φm取值范围从{0,π/2,π,3π/2}减小至{0,π},也就是说 Wm只有两种取值-1和+1。这样做对PAPR几乎没有影响,而且这是在工程和理论中常用的做法。所以文中采用此规则进行后续的算法研究。
下面对算法进行分析,得到式(5)
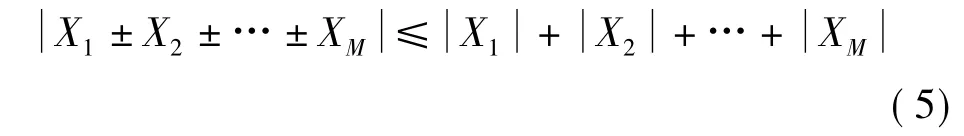
其中,Xm,m=1,2,…,M 为数据 X的分组。此不等式说明原始数据取绝对值相加必不小于将原始数据乘以相位因子后的叠加。而实际中之所以要对原始数据进行PTS处理,主要是因为原始数据直接进行叠加出现大峰值的概率较大,所以只需要特别处理较大峰值出现位置上的点,而不用关心所有的数据点。
如果记录下数据模值直接叠加后的峰值较大位置,再从原始数据中取出对应位置的值组成新数据,用新数据代替之前的原始数据,这样再进行最优相位因子的寻找,计算量将显著下降。
对上述理论分析进行仿真,如图1所示,其中横轴表示从N点原始数据中取出的采样点数P。从图1中可以看出,原始数据模值直接进行叠加后出现的峰值点位置与用传统PTS计算得到的峰值点位置相同的概率是与所取数据点数呈正比例关系,由此验证了提出的假设。

图1 原始数据峰值点位置与PTS方法处理后峰值点位置相同的概率
下面阐述新提出算法的处理步骤:
(1)对 Xm,m=1,2,…,M 进行 N 点的 IDFT 处理得到 xm,m=1,2,…,M。
(2)对 xm,m=1,2,…,M 的 N 点数据分别取模,然后将M个分组取模后进行相加得到xm′。
(3)搜索xm′中幅值最大的P个波峰值位置,构成对应的峰值位置序列{i=l1,l2,…,lp}。
(4)根据位置序列{l1,l2,…,lp}中的位置信息从xm,m=1,2,…,M 中将对应样值进行抽取,进而构造成PTS抽样序列,m=1,2,…,m;i=l1,l2,…,lp。
(5)将部分传输序列替换成PTS抽样序列,利用OPTS[4]或 IPTS[5]方法求出合适的相位因子序列。
3 计算量分析
各种算法的计算量分析如表1所示。在采用OPTS算法时,需要用2M-1个相位因子序列乘以IDFT后的N 点数据,需要做 2M-1·M·N 次乘法,2M-1·(M-1)·N次加法才能寻找到最优相位因子序列。当采用IPTS算法时,需要用M-1个相位因子序列乘以IDFT后的数据,做M2·N次乘法,M·(N-1)·N次加法寻找最优相位因子序列。当采用新提出算法,设P为采用数据的数目(P≪N),用最优化方法时,需要做2M-1·M·P 次乘法,2M-1·(M -1)·P 次加法,用次优化方法时,需要做M2·P次乘法,M·(M-1)·P次加法就可寻找到最优相位因子序列。可以看到提出的新算法在计算量方面显著减少。并且M和N越大,其优势更加的明显。

表1 各种不同算法的计算量比较
4 性能仿真
采用Matlab进行仿真,主要参数的选取如下:子载波数256;OFDM帧数10000;调制方式QPSK;相位因子{ -1,+1};分组数 M=8。图2是 IPTS,OPTS,新提出算法在分别采用最优化和次优化后的性能仿真图。图3是新提出算法取点数分别为64,128时分别采用最优化和次优化后的性能仿真图。图2和图3中的横轴代表所选取的PAPR门限。
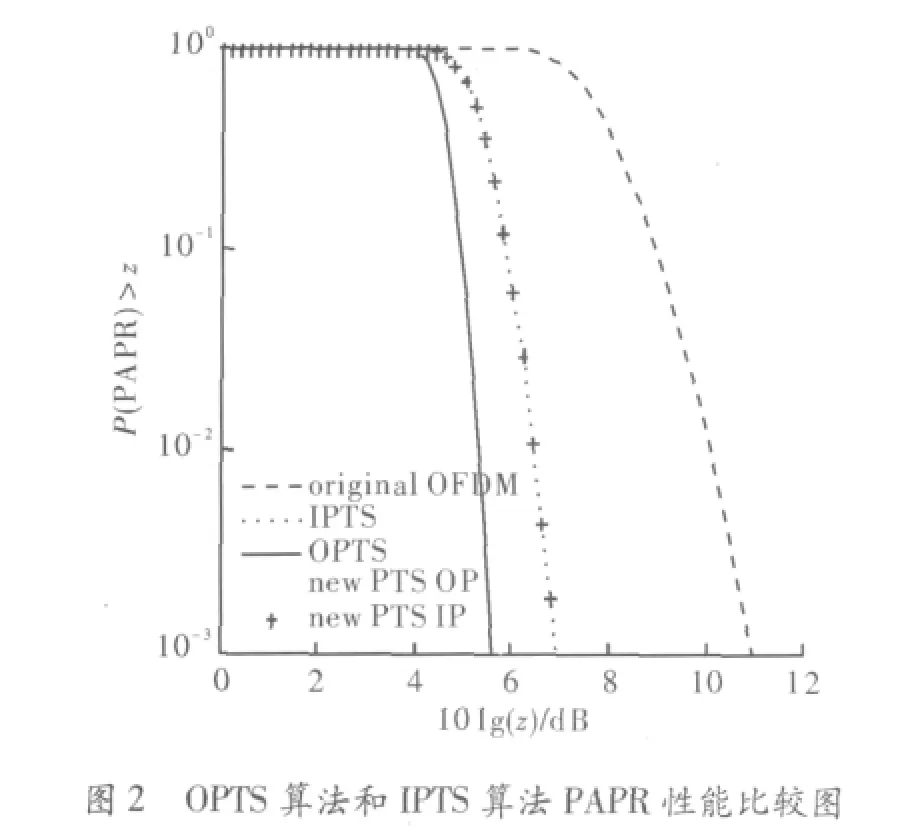
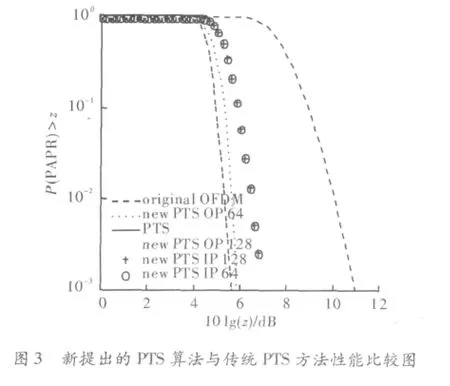
图2中只取64个点分别进行最优化和次优化算法寻找相位因子,从图中可看出文中提出的算法在采用最优化方法的性能优于IPTS,在采用次优化方法的性能基本和IPTS相当,而计算量比IPTS小。
图3中IPTS,OPTS以及新算法的分组数为8,新算法取128和64个点分别进行最优化和次优化方法寻找相位因子。从图中可看出,当点取128时的性能优于64点,并且当点取为128时,其性能接近OPTS。
5 结束语
提出一种基于PTS方法的PAPR减小算法,从性能分析和计算量分析中可以看出,新提出的算法不仅可以显著减少计算量和算法复杂度,而且可使得性能损失较小。所以总体而言,新算法有较好的应用前景。
[1]LI X D,CIMINI L J.Effects of clipping and filtering on the performance of OFDM [J].IEEE Communication Letters,19982(5):131-133.
[2]JONES A E,WILKINSON T A,BARTON S K.Block coding scheme for reduction of peak to mean envelope power ratio of multicarrier transmission scheme [J].Electronic Letter,1994,30(22):2098 -2099.
[3]SLIMANE S B.Peak-to-average power ratio reduction of OFDM signals using broadban pulse shaping[C].Vehicular Techonology Conference.2002 Proceedings.VTC 2002 -Fall,2002 IEEE 56th,2002,2:889 -893.
[4]MULLER S H,HUBER J B.OFDM with reduced peak-toaverage power ratio by optimum combination of partial transmit sequences [J].Electronic Letter,1997,33(5):368-369.
[5]CIMINI L J,SOLLENBERGER N R.Peak - to - average power ratio reduction of an OFDM signal using partial transmit sequences[J].IEEE Communications Letters,2000,4(03):86-88.
[6]HAN S H.LEE J H.PAPR reduction of OFDM signals using a reduced complexity PTS technique[J].IEEE Signal Processing Letters,2004,11(11):887 -890.
[7]KIM S S,KIM M J,GULLIVER T A.A new PTS for RAPR reduction by local search in GA[C].Piscataway:Proceedings of 2006 International Joint Conference on Neural Networks,2006:2370 -2373.
[8]LEE B M.DE FIGUEIREDO R J P.A low complexity tree algorithm for PTS-based PAPR reduction inwireless OFDM[C].Proceedings of 2006 IEEE International Conference on Acoustics,Speech,and Signal Processing.Piscataway:IEEE,2006:Ⅳ301-Ⅳ304.
[9]PISIT B,KAZUO M,TAWIL P.Proposal of improved pts method for ofdm signal[C].Greece Athens:PIMRC 2007,IEEE,2007:1 -5.
[10]YANG Lin,EMAD A.Novel low - complexity post- IFFT PAPR reduction technique by utilising amplitude transforming for OFDM systems[C].Hong Kong:Wireless Communication and NETworking Conference,2007:1339 -1343.

