基于模型试验与三维水弹性理论的船舶波激振动响应研究

汪雪良，顾学康，胡嘉骏

（中国船舶科学研究中心，江苏 无锡 214082）

基于模型试验与三维水弹性理论的船舶波激振动响应研究

汪雪良，顾学康，胡嘉骏

（中国船舶科学研究中心，江苏 无锡 214082）

船体波激振动使得船体结构中产生高频、持续和具有一定幅值的振动应力，可能引起结构发生严重的疲劳损伤，因而对船舶结构的安全性带来严峻的挑战。文章以一艘大型LNG船为研究对象，采用三维线性水弹性理论与水池模型试验方法对船舶波激振动响应进行了比较分析，研究了规则波与不规则波中的波激振动特性。改变该LNG船的刚度，并保持船型、重量分布等其它主船体特征不变，在模型试验和理论计算中探讨了刚度对波激振动的影响。通过两种刚度船体梁的模型试验与理论计算结果的比较分析，给出了波浪周期和船体刚度的变化对波激振动影响的几点结论。

波激振动；三维水弹性理论；模型试验；船体梁刚度

1 引 言

商用船舶的大型化发展趋势在跨入21世纪以来愈发明显，以往在中小型船舶中不受关注的波激振动现象越来越受到船舶结构设计人员的重视。船舶尺度逐步增大（Payer等（2006）[1]）意味着船体弹性的增大和二节点垂向振动频率的降低，从而颤振和波激振动的水弹性效应的重要性也增大（Storhaug等（2007）[2]；Wu（2007）[3]；Lijima 等（2008）[4]；Pedersen 和 Jensen（2009）[5]；Tuitman（2010）[6]）。 大型船舶在海上航行时船体梁的波激振动响应使得船体结构遭受到持续的疲劳载荷的作用，导致船舶在运营后产生严重的疲劳破坏，从而使船东付出昂贵的维修费用。

Gu等（2000）[7]采用模型试验和理论计算方法对规则波中垂向弯矩的高阶调和成分进行了研究。研究表明如果弯矩的较高阶成分等于船体梁的特征频率，则这个高阶的成分可能会导致波激振动的发生，即所谓的非线性波激振动。Dudson等（2001）[8]则提到波浪载荷的二阶或倍频成分可能会对波激振动的产生有所贡献。Jensen等（2002）[9]认为对传统的船舶来说，如果弯曲刚度小、航速高和非线性激励严重，则波激振动可能会比较严重。顾学康等（2004）[10]对一超大型油船进行了线性与非线性波激振动试验，对油船波激振动响应特征及其对结构疲劳的贡献进行了研究。通过试验发现，零航速时，按波浪遭遇频率变化的低频波浪弯矩能量较大，占主要成分，其它为一些倍频成分；有航速时，按船体梁一阶振动频率变化的高频波浪弯矩占主要成分，比波浪遭遇频率的能量大得多。通过分析，作者认为船体梁一阶总振动频率与波浪遭遇频率之间的倍数关系（n）使船体梁产生共振，即非线性波激振动。

Wang等（2010）[11]采用模型试验方法对一艘50万吨级的超大型矿砂船的波激振动响应进行了研究。研究表明船舶的装载状态对波激振动的产生有显著的影响，且压载状态较满载状态时的波激振动响应大。汪雪良等（2010）[12]研究了环境与航行参数对该超大型矿砂船波激振动预报的影响，并与模型试验结果进行了比较。Hu等（2012）[13]用三维线性与非线性水弹性理论与相应的数值方法研究了该船在波浪中的高频载荷响应，给出了线性和二阶非线性水弹性响应的理论预报及与拖曳水池模型试验结果的比较。同时分析了航速对波浪载荷和结构响应的影响。结果表明，波浪周期较短时即使波高较小，该船亦易于产生波激振动。波高较大时，船体往往同时产生波激振动和砰击引起的振颤。

大型LNG船作为一种高附加值船型，近几年其大型化发展趋势也十分迅猛，国内正在开发的22万方大型LNG船的船长已经超过了320 m。毫无疑问，这样的大型船舶在海上航行时的波激振动现象应该得到设计人员的重视。本文通过三维水弹性理论及水池模型试验方法对一艘15.68万方的大型LNG船的波激振动进行了理论预报和模型试验研究，并通过改变船体梁的刚度研究其对波激振动响应的影响。

2 三维水弹性理论方法

上个世纪70年代中期，各种用于分析大型海洋浮式结构物耐波性问题的三维水动力学方法随着大型计算机的出现而相继得到快速发展，Wu[14]将三维适航性理论与三维结构动力学理论相结合，提出了广义流固界面条件，发展了一个适用于分析波浪中任意三维可变形体承受内、外激励时动响应性能的三维水弹性理论。

在过去的二十多年里，三维水弹性理论已经在多种船舶与海洋工程结构的设计研究中得到了应用，如王志军（2001）[14]、Hirdaris 等（2003）[15]、Remy 等（2006）[16]、Malenica 等（2008）[17]、Kim 等（2008）[18]、Tian等（2009）[19]和Hu等（2012）[13]。下面对三维线性水弹性理论作一个简要的叙述。

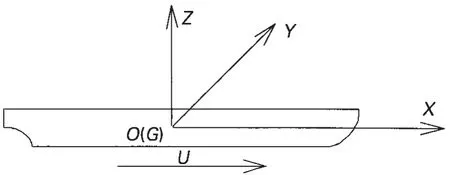
图1 平衡坐标系的定义Fig.1 Definition of synchronous coordinate system

如图1，在平衡坐标系Oxyz中，Oxy平面位于未扰动的静水面上，x轴从船尾指向船首，y轴指向左舷，z轴向上并通过重心G，船体上任意一点的位移可以表达为

在本文的研究中，船体梁干结构模型简化为一根两端自由的变截面铁木辛柯（Timoshenko）梁，在结构有限元模型的对称模态分析和反对称模态分析中，可以求得各模态下梁上各横截面上有限元节点的集中力。记梁的第r个模态、第i个节点上的垂向力和力矩的主模态为Fz（ir）和Mz（ir），单元节点坐标记为（xi,yi,zi），i=1,2,…,NT，NT为梁的节点数。设在水弹性分析中共考虑m个模态，垂向集中力和力矩分别记为Fz和Mz，从而可以得到在规则波激励下船体梁上力与力矩主模态为：

式中，r为第7,…,m阶弹性模态，p（r）为第r阶模态的主坐标，ωe为波浪的遭遇频率。

在线性水弹性理论（Price 和 Wu（1985）[21]；Bishop 等（1986）[20]）中，（1）式的一阶形式可以表达为：

当船舶以航速U、浪向角β（180°为顶浪）在能量谱为Sζ（ω）的单一方向传播的不规则波中航行时，船舶遭遇的波浪频率为ωe=ω（ 1-Uωcosβ/g），遭遇波浪的幅值可以表达为N个频率成分规则波的组合，每一个频率的带宽均为Δωej，随机相位角为εj：

这样，一阶速度势和主坐标可分别表达为：

传统的辐射势可用边界积分法表达为：

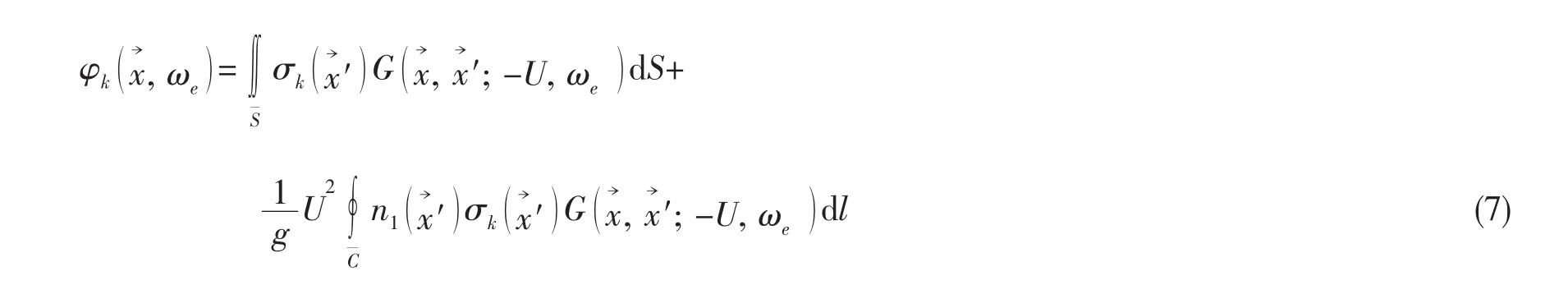
其中，G 为频域 Green 函数，σk为源强，={x′ ,y ′,z′}为源点的坐标，和分别为船舶在其定常位置时的平均湿表面和水线。辐射势必须满足船体表面边界条件：

φ可在某前进航速下进行计算，φo、φD在指定的浪向角和频率下进行计算，φk则对要求的主坐标模态进行计算。

因而运动方程可以表达为如下的广义矩阵形式：

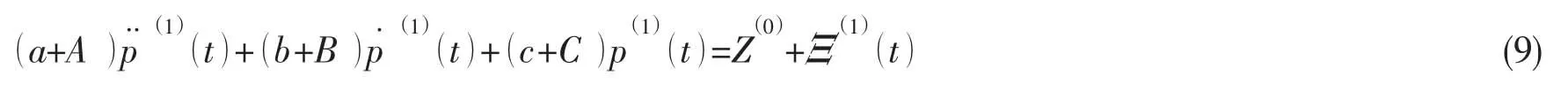
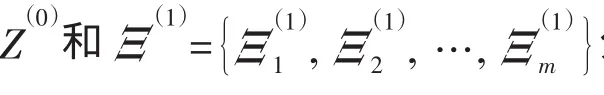
广义的水动力附加质量和阻尼系数满足（10）式：

广义回复力系数满足（11）式：

第r阶模态的广义定常力满足（12）式：

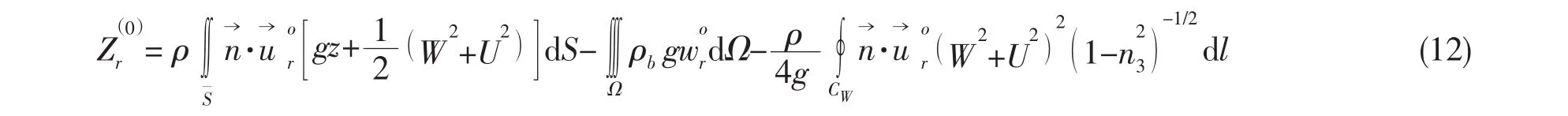
第r阶模态的一阶广义波浪力满足（13）式：

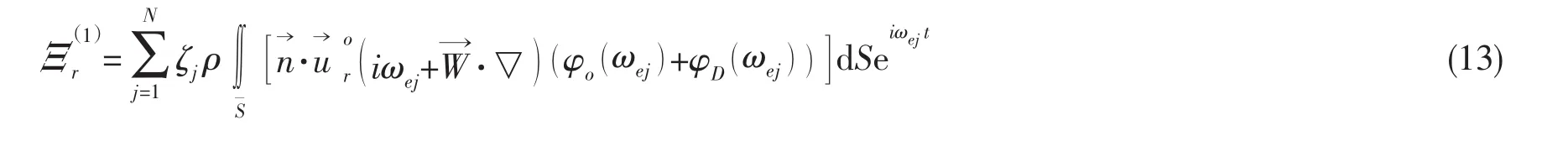
3 水池模型试验方法

本文研究的15.68万方大型LNG船可能会在较低海况下产生船体较大幅度的二节点振动现象，即波激振动。模型根据实船压载状态进行缩放加工，在模型的第2、4、6、8、10、12、14、16和18站分段，以测量分段处的垂向弯矩。该大型LNG实船主尺度见表1，横剖面型线图见图2，图3为龙骨梁分段模型示意图。模型的刚度均以实船的舯剖面刚度按照缩尺的5次方的关系进行缩放。为了研究刚度变化对波激振动的影响，根据原始模型的船体梁一阶振动频率的理论计算值缩小3倍后进行反推得到小刚度模型的刚度。

图2 横剖面型线图Fig.2 Body planes

图3 龙骨梁分段模型示意图Fig.3 Sketch map of the segmented model

4 理论计算与模型试验结果的比较

表1 主尺度Tab.1 Main particulars

4.1 船体梁垂向振动特性

采用三维水弹性理论对船舶的垂向振动固有频率进行计算时，以非均匀截面的Timoshenko梁作为干结构进行模态分析。在通用有限元软件中进行建模并进行模态分析，从而得到该梁在真空中的振型等模态信息。图4为该梁在真空中的二节点、三节点和四节点垂向弯曲振型图。

三维水弹性计算中选取湿表面以下的船体外壳为湿结构，图5为湿结构的网格模型。水弹性计算的干结构的节点数为21个，单元为20个；湿结构节点数为1 058个，网格数为900个。

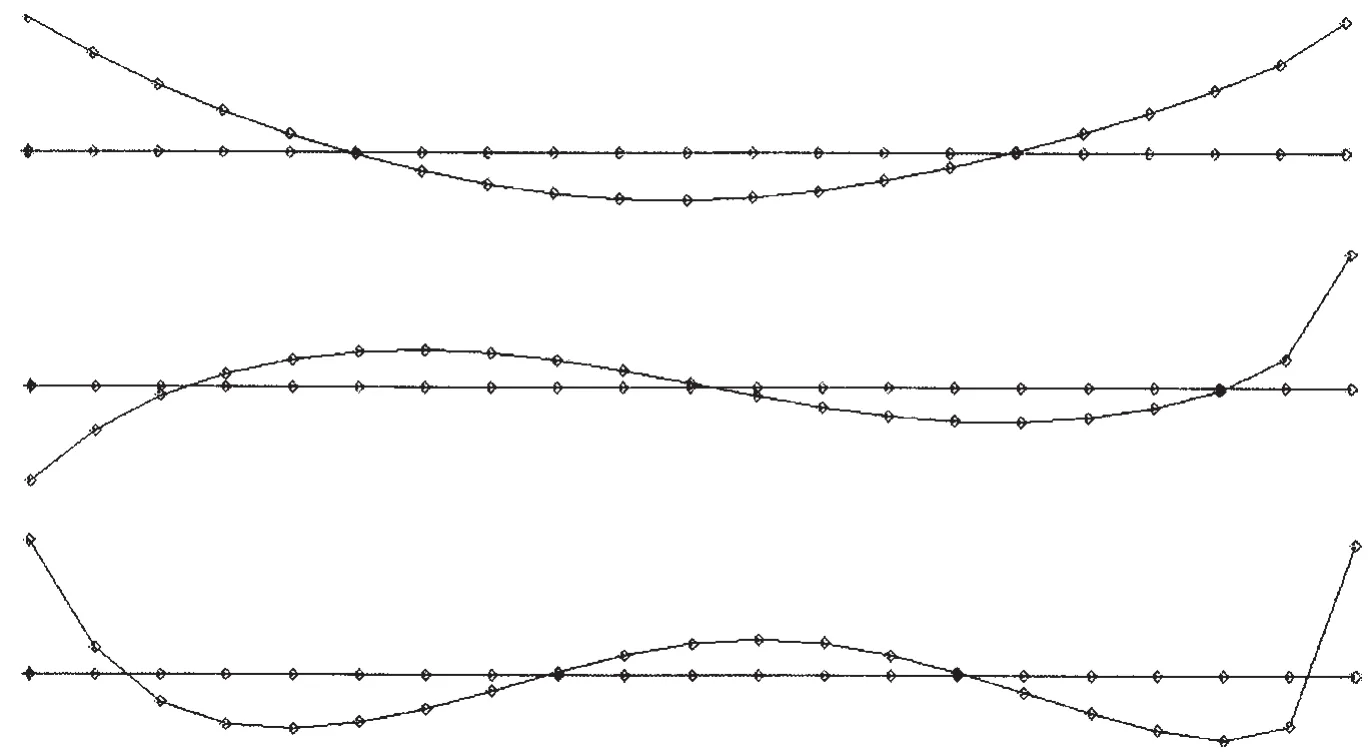
图4 大型LNG船干结构在真空中二节点、三节点和四节点垂向弯曲振型Fig.4 2-node,3-node and 4-node modal shapes of vertical bending for a large LNG carrier’s dry structure in vacuum

图5 大型LNG船三维水弹性计算的湿结构网格模型Fig.5 Gridding model of wet structure for a large LNG carrier in 3D hydroelastic calculations

图6为原始刚度的大型LNG船在航速U为19.5 kns、浪向β为180°时的三维水弹性计算得到的二节点和三节点垂向弯曲主坐标传递函数。由表2可见，对船体垂向弯曲起主要作用的二节点垂向振动频率的三维水弹性计算结果与试验结果吻合很好，三节点垂向振动频率的偏差也小于10%。

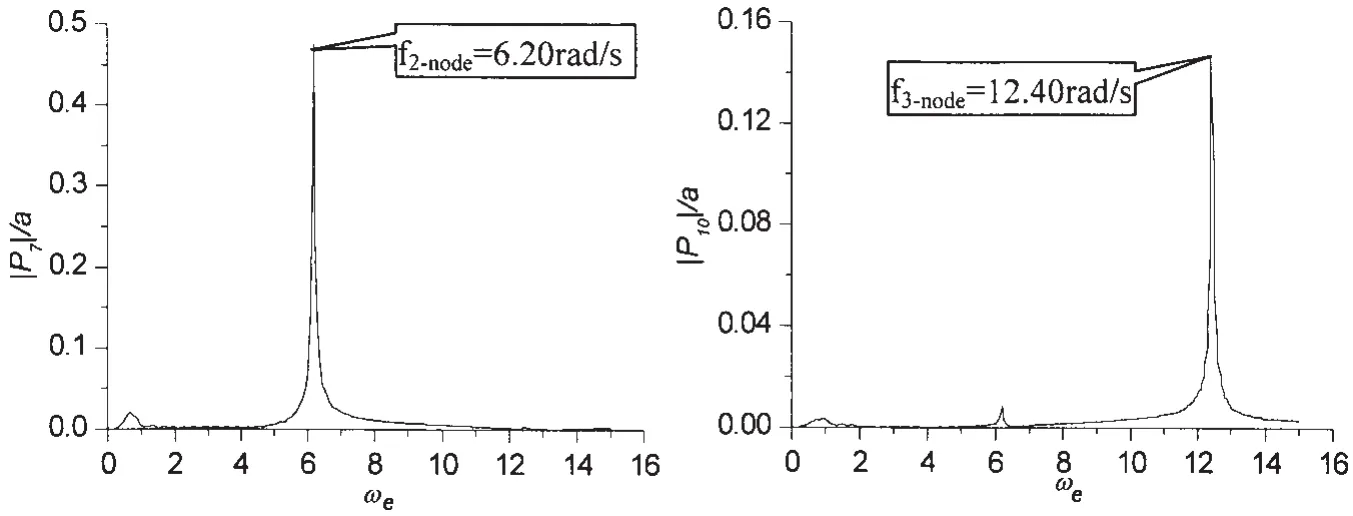
图6 原始刚度船体梁二节点和三节点垂向弯曲主坐标传递函数（U=19.5 kns，β=180°）Fig.6 RAOs of the principle coordinates of 2-node and 3-node vertical bending in original hull girder stiffness(U=19.5kns,β=180°)

表2 原始刚度船体梁垂向振动频率理论计算和模型试验结果的比较（换算到实船）Tab.2 Comparison between theoretical and experimental results of vertical bending frequencies in original hull girder stiffness(in full scale)

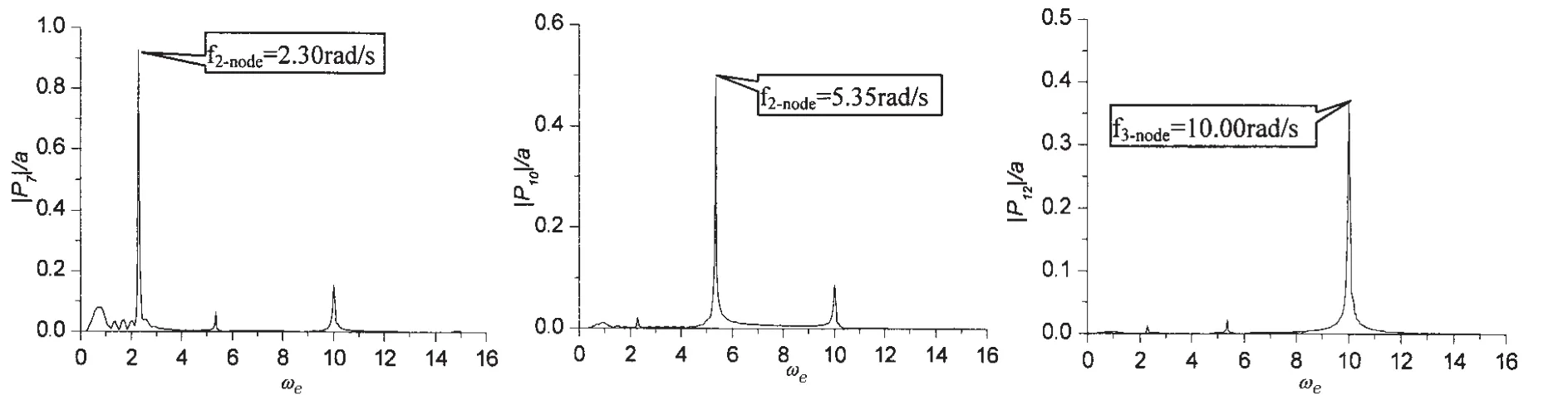
图7 小刚度船体梁二节点、三节点和四节点垂向弯曲主坐标传递函数（U=19.5kns，β=180°）Fig.7 RAOs of the principle coordinates of 2-node,3-node and 4-node vertical bending in small hull girder stiffness(U=19.5kns,β=180°)

表3 小刚度船体梁垂向振动频率理论计算和模型试验结果的比较（换算到实船）Tab.3 Comparison between theoretical and experimental results of vertical bending frequencies in small hull girder stiffness(in full scale)

大型LNG船变刚度状态指船体梁的刚度按照原型船船体梁二节点垂向振动频率的1/3来进行刚度的缩减，由此，大型LNG船实船刚度改变后舯剖面惯性矩I约为原始舯剖面惯性矩的11%，即人为使得船体的刚度和频率有了大幅的减小，在此基础上通过模型试验和理论计算研究船体梁刚度或频率对船体波激振动响应的影响。三维水弹性理论计算的二节点、三节点和四节点垂向弯曲主坐标传递函数见图7。由表3可见，二节点和三节点垂向振动频率的三维水弹性计算结果与试验结果吻合很好，偏差在5%以内，四节点垂向振动频率的偏差也小于10%。比较表2和表3可以发现，船体梁刚度减小到原来的11%以后，二节点垂向振动频率减小到原来的37%，变刚度船体模型设计时船体梁一阶垂向振动频率为原始刚度的1/3即33.3%，由此可以得到理论计算和模型设计的偏差为3.8%，这从另一方面说明三维水弹性理论计算验证了变刚度模型设计的正确性。

4.2 规则波中的响应

在规则波的激励下，图8给出了原始刚度的大型LNG船在航速U=19.5 kns，浪向β为180°时的垂向弯矩传递函数，其中实线为三维线性水弹性的计算结果，虚线为二维非线性切片理论（NORSFAT）的计算结果，圆圈为模型试验的波频弯矩值WM，三角形为模型试验的合成弯矩值CM。NORSFAT是顾学康（1999）[23]发展的一个预报船舶在高海况下非线性响应的切片理论程序，从工程实用的角度出发,探索船体在海上作大幅运动时，由于船体的非直壁引起的非线性波浪弯矩响应，并将船体作为弹性梁，预报其在高浪级下的非线性合成弯矩，并解决了波浪诱导弯矩与砰击弯矩相互迭加的相位问题。从该图可以看出，三维水弹性理论与二维非线性切片理论预报精度相当。试验值显示，在无因次遭遇频率为 3.9（λ/L=0.9）附近有峰值之外，在 7.0（λ/L=0.4）附近还有一个次峰值。理论预报的结果也显示了这个峰值（尽管峰值位置稍有偏差），但是幅值几乎要较模型试验值小一倍，这显示了模型试验中船体遭受的高频时的波频激励效应没能在理论预报中完全反映出来。

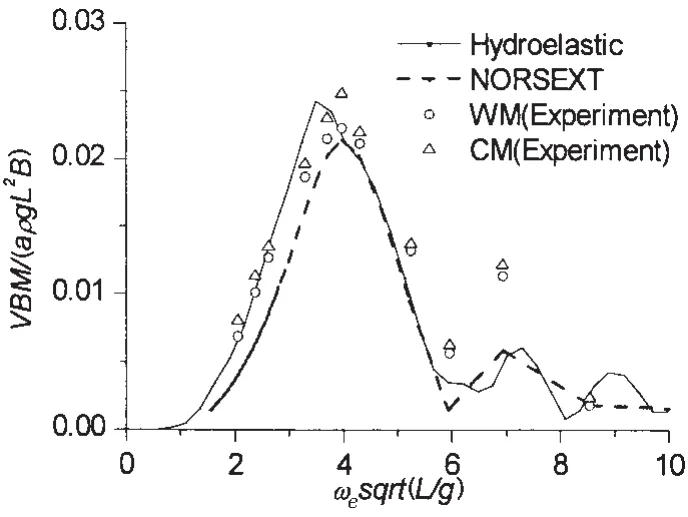
图8 原始刚度下舯剖面垂向弯矩传递函数（U=19.5 kns，β=180°）Fig.8 RAOs of vertical bending moments at the midship section in original hull girder stiffness(U=19.5 kns,β=180°)

类似地，图9是小刚度的大型LNG船舯剖面垂向弯矩传递函数（U=19.5 kns，β=180°），右图为左图的局部放大。与原始刚度状态类似，试验结果中由倍频引起的次峰值在水弹性的预报中没有得到充分的反映（此处在模型试验中有倍频，但三维水弹性理论计算中没有，因为是线性理论）。三维水弹性理论还对更高频率下的谐振峰值进行了预报，如ωesqrt L/（）g 分别为11.9、24.3和37.5处传递函数的谐振峰值，由于造波设备能力的限制，这些高频谐振现象未能在模型试验结果中得到反映。另一方面，从三维水弹性和二维非线性切片理论的预报结果来看，两者在低频部分（ωesqrt L/（）g ＜6.0左右）的预报精度是相当的，在原始刚度下的计算比较中也验证了这一点。

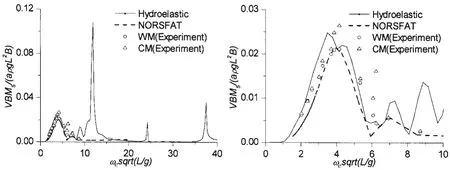
图9 小刚度下舯剖面垂向弯矩传递函数（U=19.5 kns，β=180°）Fig.9 RAOs of vertical bending moments at the midship section in small hull girder stiffness(U=19.5 kns,β=180°)

两种刚度下大型LNG船舯剖面垂向弯矩传递函数的三维水弹性计算的比较见图10，OS表示原始刚度，SS表示小刚度。从图上可以看出，两种刚度下低频遭遇波浪下的响应是很接近的。右图中两种刚度下的第二个和第三个次峰值依次对应于遭遇波浪频率的约2倍和3倍的关系，这两个频率是高频时波频响应特性的反映，所对应的载荷响应的差异体现了刚度变化对载荷响应的影响，即刚度的减小使得高频时波频对应的载荷响应增大，对应两个频率下由刚度的变化导致的垂向弯矩响应分别增大了56%和219%。左图显示两种刚度下更高的波浪遭遇频率所对应的垂向弯矩响应幅值有着巨大的差异，这种差异可能与理论计算中结构阻尼（两种刚度下结构阻尼均取0.05）的选取相关，实际上这样高的波浪频率的海浪在实际的海洋环境中是不存在的，但峰值出现的位置的差异也从数值计算方面反映了刚度的变化对船体垂向弯曲响应（更高阶波激振动）的影响程度。

图10 大型LNG船舯剖面垂向弯矩传递函数在两种刚度下的比较（U=19.5 kns，β=180°，其中右图为左图低频弯矩成分的放大）Fig.10 Comparison of RAOs of vertical bending moments for a large LNG carrier in two kind of hull girder stiffness(U=19.5 kns,β=180°,the right figure is the magnification of the low frequency part in left figure which is presented by a dot circle)

4.3 不规则波中的响应

大型LNG船原始刚度模型和小刚度模型的不规则波试验皆针对低海况（模型有义波高Hs=50 mm，波浪特征周期 Tz=0.813 s、1.303 s和 1.750 s；对应实船 Hs=2.5 m，Tz=5.748 s、9.214 s和 12.374 s）时的波激振动研究而设计，因而试验中没有砰击现象发生。

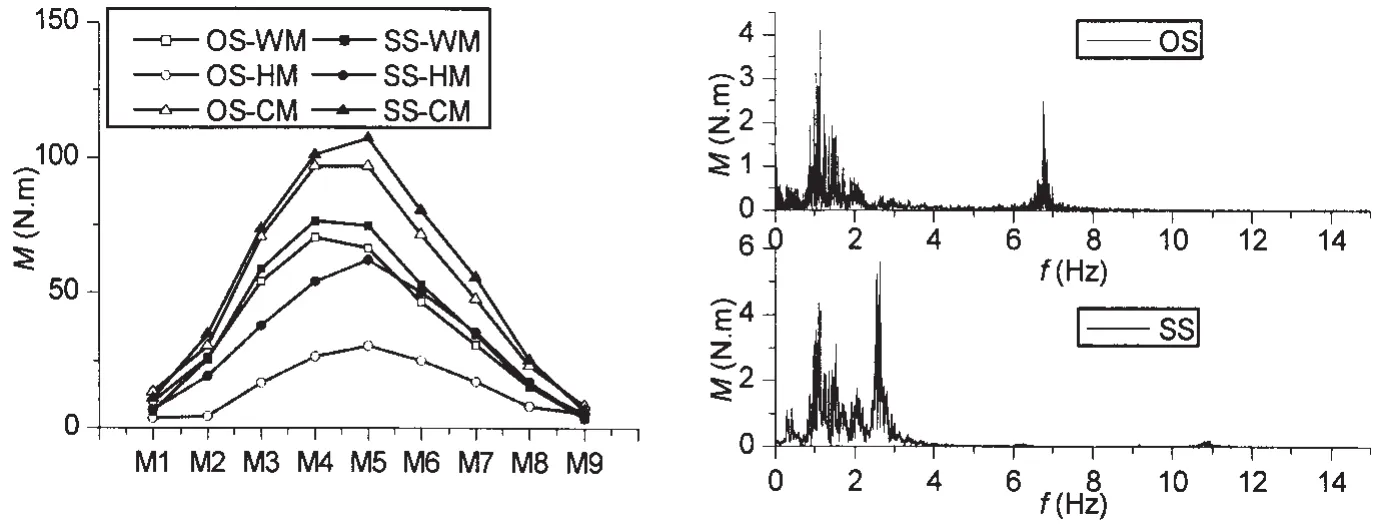
图11 波浪周期Tz=0.813 s时垂向弯矩各成分及频谱图的比较Fig.11 Components of vertical bending moments and their frequency distributions at Tz=0.813 s

图12 波浪周期Tz=1.303 s时垂向弯矩各成分及频谱图的比较Fig.12 Components of vertical bending moments and their frequency distributions at Tz=1.303 s

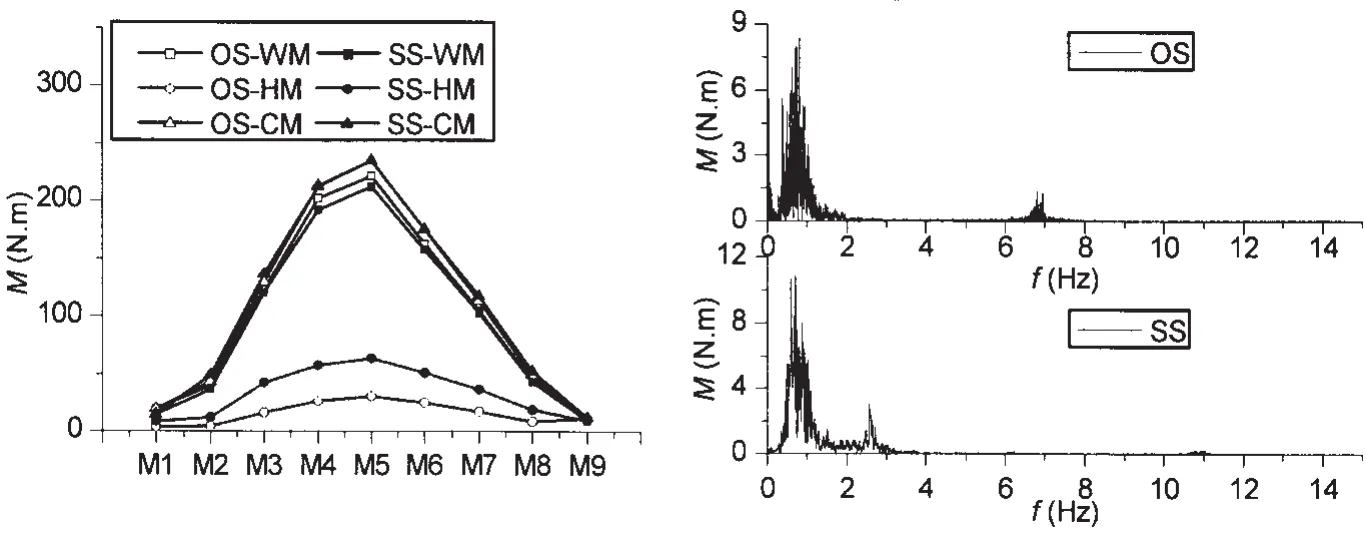
图13 波浪周期Tz=1.750 s时垂向弯矩各成分及频谱图的比较Fig.13 Components of vertical bending moments and their frequency distributions at Tz=1.750 s

不同Tz时两种刚度模型的波浪矩WM、高阶矩HM和合成矩CM的试验有义值的比较和频谱图的比较见图11-13。所有试验值均为换算到了Hs=50.0 mm时的数值。可以看出，在三种Tz下，刚度的减小使得WM、HM与CM都有所增大，且随着Tz的减小，小刚度引起的载荷增加比值逐渐增大。此外，HM增大的绝对值在Tz为1.303 s（实船为9.214 s）时最大。从频谱图可以看出，小刚度时船体梁的二节点垂向振动频率峰值更加靠近载荷的遭遇波浪频率成分峰值，可以预见，随着波浪周期的进一步减小，或者船体梁刚度的进一步降低，或是船长的进一步增大，船体梁的二节点垂向振动频率与遭遇波浪频率会产生部分重叠、全部重叠甚至是船体梁的垂向振动频率小于遭遇波浪频率的现象，这将为从CM中分离出WM和HM带来了困难。如果出现船体梁的垂向振动频率小于遭遇波浪频率的情况，则传统意义上载荷的WM、HM和CM可能要重新定义。由上述分析可见，波激振动发生与否不仅与船体梁刚度相关，还与遭遇的波浪周期息息相关。

不同波浪周期时两种刚度下理论计算的垂向弯矩时间历程曲线见图14。由图可见，小刚度下理论计算的垂向弯矩时间历程曲线呈现出了波激振动现象，波浪周期较小（Tz=5.748 s）时尤其明显，而原始刚度的曲线即使在Tz=5.748 s时也只呈现了略微的波激振动现象，随着波浪周期的增大，如Tz=12.374 s（模型Tz=1.750 s）时，原始刚度的时间历程曲线中已经看不出波激振动现象了。

图14 不同波浪周期时两种刚度下理论计算的垂向弯矩时间历程曲线Fig.14 Time history curves of vertical bending moments from theoretical calculations with different wave periods in two kinds of hull girder stiffness

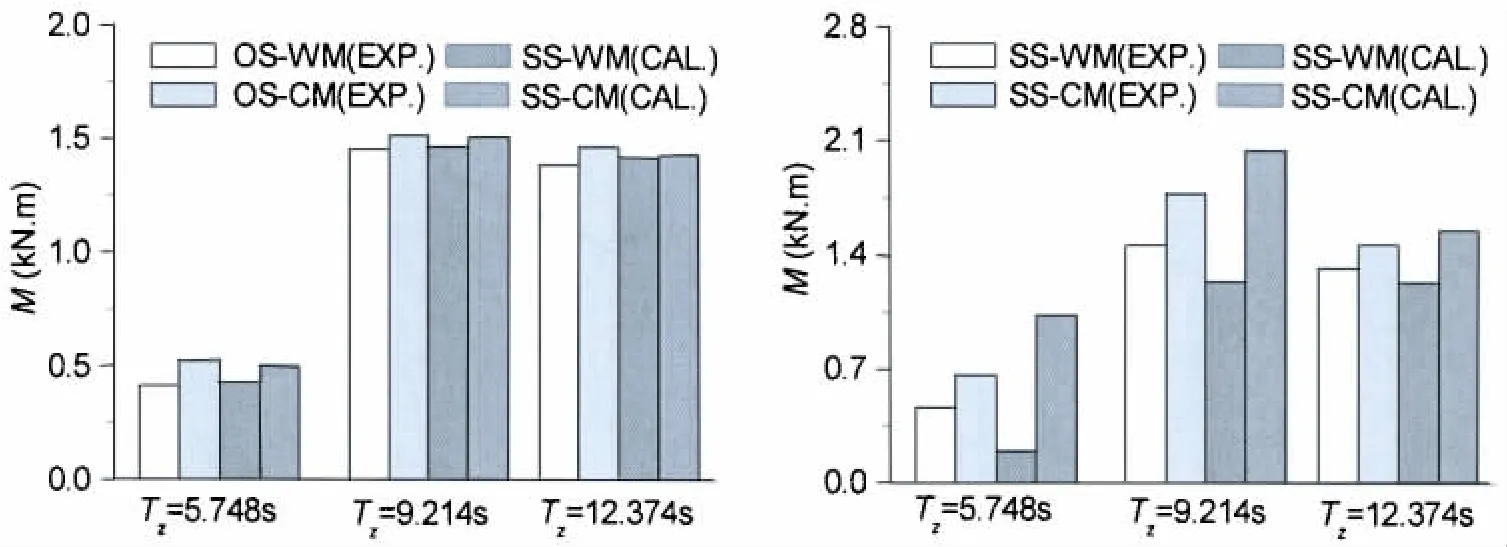
图15 不同波浪周期时两种刚度下理论计算的垂向弯矩直方图的比较Fig.15 Comparison of histograms of vertical bending moments from theoretical calculations with different wave periods in two kinds of hull girder stiffness

不同波浪周期时两种刚度下理论计算的垂向弯矩直方图的比较见图15。从左图上可以看出，原始刚度（OS）下，理论计算的WM和CM均与试验值符合良好，三个波浪周期下，WM与CM的差异均不大，这说明载荷成分中高阶成分的占比是小量；从右图可以看出，小刚度（SS）下，理论计算的WM和CM值与模型试验值均存在着一定的差异，且波浪周期较小时，这种差异更显著，即小周期时，理论计算的计算结果更加突出了波激振动的特性。从两种刚度下模型试验结果和理论计算结果来看，波激振动的特性随着波浪周期的减小变得更加显著，并且结构刚度变小使得船体更易于产生波激振动。

5 结 论

本文通过15.68万方大型LNG船波激振动模型试验和三维水弹性理论计算结果的比较分析，研究了大型LNG船的波激振动特性，并通过减小原始船体的刚度，研究刚度的变化对波激振动的影响。通过研究可以得到如下结论：

（1）采用梁模型作为干结构进行模态分析的三维水弹性理论在船体波激振动响应的预报方面具有良好的精度，预报结果合理可信。二维非线性切片理论与三维水弹性理论在低频区域对波浪载荷的预报精度相当。

（2）船体结构刚度的减小不仅使得船体的垂向振动频率减小，还使得倍频对应的载荷响应增大，从而导致更加严重的波激振动现象。这种倍频的作用在模型试验中得到了充分的反映。

（3）小刚度时船体梁的二节点垂向振动频率更加靠近遭遇波浪频率，可以预见，随着波浪周期的进一步减小，或者船体梁刚度的进一步降低，船体梁的二节点垂向振动频率与遭遇波浪频率可能会产生部分重叠、全部重叠甚至是船体梁的垂向振动频率小于遭遇波浪频率的现象，这将对超大型船舶与海洋工程结构物的载荷特性的分析处理方法提出了新的要求。

[1]Payer H G,Brostella R.The Panama Canal expansion and the Panamax vessels of the future[C]//In:Transactions Society of Naval Architects and Marine Engineers.Fort Lauderdale,US,2006.

[2]Storhaug G.Experimental investigation of wave induced vibration and their effect on the fatigue loading of ships[D].Ph.D thesis,Norwegian University of Science and Technology,2007.

[3]Wu M K,Moan T.Sensitivity of extreme hydroelastic load effects to changes in ship hull stiffness and structural damping[J].Ocean Engineering,2007,32:1745-1756.

[4]Iijima K,Yao T,Moan T.Structural responses of a ship in severe seas considering global hydro-elastic vibrations[J].Marine Structures,2008,21:420-445.

[5]Pedersen P T,Jensen J J.Estimation of hull girder vertical bending moments including non-linear and flexibility effects using closed form expressions[J].Proceeding of IMechE,Part M:J Engineering for the Maritime Environement,2009,223(3):377-390.

[6]Tuiman J T.Hydro-elastic responses of ship structure to slamming induced whipping[D].PH.D dissertation,Technical U-niversity of Delft,2010.

[7]Gu X K,Shen J W,Moan T.Experimental and theoretical investigation of higher order harmonic components of nonlinear bending moments of ships[J].Journal of Ship Technology Research,Schiffstechnik,2000,47(4):143-154.

[8]Dudson E,Rambech H J,Wu M K.Determination of wave bending loads on a 40 knots,long slender open topped containership through model tests and hydrodynamic calculations with particular reference to the effects of hull flexibility on fatigue life[C]//Proceedings of the 6th International Conference on Fast Sea Transportation.Southampton,UK,2001,2:177-190.

[9]Jensen J J,Vidic-Perunovic J.On springing of mono-hull ships[R].DNV Workshop on Fatigue Strength Analysis of Ships,Finland,2002.

[10]顾学康,胡嘉骏.超大型油船模型波浪载荷试验报告[R].无锡:中国船舶科学研究中心科技报告,2004.

[11]Wang X L,Gu X K,Hu J J,Xu C.Experimental investigation of springing responses of an ultra large ore carrier[C]//The 9th International Symposium on Practical Design of Ships and Other Floating Structures.Rio de Janeiro,RJ,Brazil,2010:1325-1334.

[12]汪雪良,胡嘉骏,顾学康,张 凡.超大型矿砂船波激振动及颤振研究[J].江苏科技大学学报,2010,24(2):120-124.

[13]Hu J J,Wu Y S,Tian C,Wang X L,Zhang F.Hydroelastic analysis and model tests on the structural responses and fatigue behaviors of an ultra-large ore carrier in waves[J].Proceeding of the Institution of Mechanical Engineers,Part M:Journal of Engineering of the Maritime Environment,2012,226(1):1-21.

[14]Wu Y S.Hydroelasticity of floating bodies[D].PH.D thesis,Brunel University,1984．

[15]王志军.箱式超大型浮体结构的水弹性响应研究[D].上海:上海交通大学,2001.

[16]Hirdaris S E,Price W G,Temarel P.Two-and three-dimensional hydroelastic modeling of a bulker in regular waves[J].Marine Structures,2003,16(8):627-658.

[17]Remy F,Molin B,Ledoux A.Experimental and numerical study of the wave response of a flexible barge[C]//Proceedings of the 4th International Conference of Hydroelasticoty in Marine Technology.Wuxi,China,2006:255-264.

[18]Malenica S,Senjanovic I,Tomasevic S,Stumpf E.Some aspects of hydroelastic issues in the design of ultra large container ships[C]//Proceedings of the 23rd International Workshop on Water Waves and Floating Bodies IWWWFB.Korea,2008.

[19]Kim Y,Kim Y.Analysis of springing effects on floating barges in time domain by a fully coupled hybrid BEM-FEM[C]//Proceedings of the 23rd International Workshop on Water Waves and Floating Bodies IWWWFB.Korea,2008.

[20]Tian C,Wu Y S,Chen Y Q.The hydroelastic responses of A large bulk carrier in waves[C]//Proceedings of the 5th International Conference on Hydroelasticity.Southampton,UK,2009.

[21]Bishop R E D,Price W G,Wu Y S.A general linear hydroelasticity theory of floating structures moving in a seaway[J].Philosophical Transactions of the Royal Society of London.Seriea A.Mathematical and Physical Sciences,Royal Society(Great Britain),1986,316(1538):375-426.

[22]Price W G,Wu Y S.Hydroelasticity of marine structures[C]//The 16th International Congress of Theoretical and Applied Mechanics(IUTAM).Lyngby,Denmark:Sectional Lecture,S-10,1985.

[23]顾学康.船舶结构的直接设计[D].无锡:中国船舶科学研究中心,1999.

Springing investigation of a ship based on model tests and 3D hydroelastic theory

WANG Xue-liang,GU Xue-kang,HU Jia-jun
(China Ship Scientific Research Center,Wuxi 214082,China)

Springing responses will induce continuous vibrating stresses,with high frequencies and certain amplitudes,in ship structures.Thus serious fatigue damage might appear in ship structures and the safety of ship structures might be severely threatened.The comparison of springing responses,based on 3D hydroelasticity theory and model tests,of a large LNG carrier both in regular and irregular waves was presented in this paper.In order to study the influence of hull girder stiffness on springing,the original stiffness of the LNG carrier was reduced,but other main particulars such as bodyline and weight distribution were not changed.Several conclusions are made about the effects of wave periods and hull girder stiffness on springing responses according to the comparison of experimental and theoretical results of the LNG carriers with different stiffness.

springing;3D hydroelasticity theory;model test;hull girder stiffness

U661.4

A

1007-7294（2012）08-0915-11

2012-05-09

汪雪良（1977-），男，高级工程师，博士生；顾学康（1963-），男，研究员。